相対論的運動学
                        竹下徹　：　　信州大学　理学部　物理科学科　：　 mail to  tohru@shinshu-u.ac.jp
一粒子


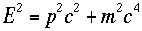
これを当たり前として出発(そうでない人はLorentz 変換の項を参照してください）。この式は一粒子の静止質量=、3元運動量=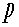（ベクトルとして扱うべきであるが表記は二乗されているので、大きさを示し同 じ意味である）, 全エネルギー=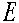 の間に成り立つ関係式である。静止質量は粒子固有の量で不変（Lorentz 変換の所で述べる意味のLorentz 不変　と言うのが物理用語である）である。ある粒子のエネルギー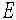と運 動量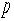を独立に測定できたなら、その粒子の質量は、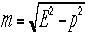で計算できるとも嫁有る。ちなみに c=1の単位系を使うと次のように書ける、　。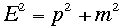
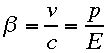　とβを定義する。ここでvは静止系（あたなの立っているいる座標 系）からみた粒子の速さである。相対性理論の前提条件１として光速=cは速度の最大値と決めるので、β=<1 は明らかである、ちなみに等号は m=0の時に成立。このβを速さと呼ぶこともある。βだけでは計算が便利にならないのでγを定義して用いる。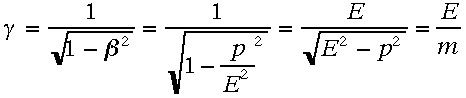

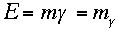
上の式を書き直して　　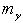を相対論的質量ということもある。ここではc=1のunitだが、これを戻 すと、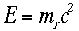で有名なアインシュタインの公式である。この式は速さvで走 る（これを静止系からみていると）粒子の質量はあたかも静止質量のγ倍になったかのごとく見える！というものだ。なに？質量は変化するのか？って、式の中 に現れる質量として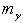を用いるなら速さが大きくなるとその意味の「質 量」は大きくなるのだ！ただし普通は静止質量と質量を同等扱いしているので注意が必要。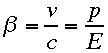この式の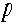は運動量で、通常の世界（ニュートン運動、あるいは古典論の世界＝高校物理 と大学の１年生までの物理）の量で質量ｘ速さである。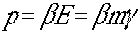
であるから相対性理論における運動量は速さ（β）ｘ質量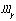（）となっている。
これの古典論極限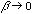（）を取ってみる。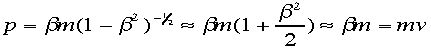
運動量の通常（古典的な）の表現と一致する。すなわち相対性理論は古典論（ニュートン力学）をそのv<<cの極限で含んでいる事が判る。

運動エネルギーTは全エネルギーと静止エネルギーの差としてつぎの式となる。

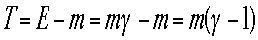
この式の非相対論的（古典論）近似を行い通常の力学の運動エネルギー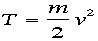と 一致する事を確かめる。古典論では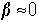であり、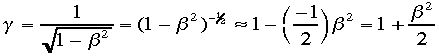

と近似できる。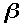はc=1の系では速度vであることに注意。よって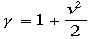
運動エネルギー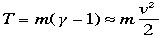と相対論と古典力学は近似で一致する。

二粒子系
質量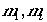の二粒子が作る系を考える。色々な慣性系があるが、代表的なも のは、実験室系と重心系である。粒子１の３元運動量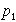とエネルギー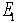、粒子２についても同様に３元運動量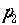とエネルギー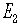とする、上の式はやはり成立する。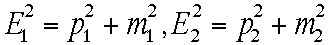

また次の量が有用である。四元運動量（エネルギー・運動量ベクトル）の所でも述べたように、sはLorentz不変である。すなわちどの慣性系でこの量を 計算しても同じ値を取る。


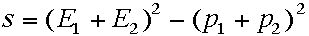
実験室系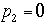：の系であ る。従って粒子１が運動量（断らない限り運動量は三元運動量の大きさをいう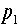）、エネルギー（これをエネルギーとは相対論的全エネルギーである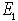）で静止したターゲット粒子２運動量ゼロ、エネルギーm2　にぶつかる場面で ある。
ここで量sをこの系で計算しておく。


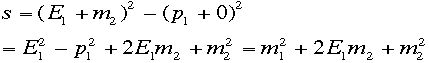
重心系：この系では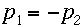が 成り立つ。つまり運動量中心系と呼ぶべきであるが、歴史的に重心系と呼ばれている。ここでsを計算すると、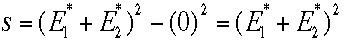

が成り立つ。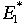,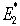のように*(アスタリスク）を付けたのは重心系であることをあからさまに示 すためである。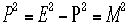の式の意味はここではまた重要である。二粒子の作る 系を一つのものと捕らえて運動量をP（大文字）、エネルギーを　E, 質量をM （大文字）とするとこの式となる。ここで二つの粒子の質量の二乗がこの重心系ではs²に一致するので、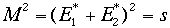となる。即ち重心系では衝突の全エネルギー（つまりE₁*+E₂*) が２粒子系の全質量=Mに等しいのだ。なにか粒子を作り出すときその質量がMならば、必要なエネルギーは重心系でE₁*+E₂* である。そしてまたそのMはsとも等しいので、Lorentz不変量sはどの系で計算しても同じ値だから、これを粒子１個を作り出すことに全勢力をつぎ込 む系つまり重心系に持っていっても同じだから、sを恒に計算すれば良いことが判る。運動量は相殺されて粒子を作り出す時にエネルギーとしては寄与しない。

例題：実験室系で入射運動エネルギーA(GeV)で陽子（質量1GeV)が陽子ターゲットにはいるととしよう。π粒子が生成される最低の入射エネルギーは いくらか？また反陽子が生成される最低の入射エネルギーはいくらか？（陽子数保存を仮定すること）

実験室系と重心系をつなぐ相対速度あるいはβを計算しておく、
一粒子では　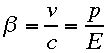であり、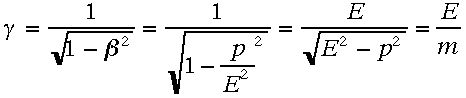であった。そこから運動量pとエネルギーEをつぎのように書き下せた。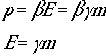二粒子系で同様の定義をおこなう。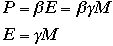という計算ができて、ここでPとEは２粒子系の全体が持つ運動量とエネル ギーである。ここでのβ,は重心系という座標系の実験室系に対する相対速度である。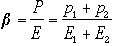の式の右辺を実験室系の量で書きくだせばβは実験室系からみた重心系の速度 となる。従って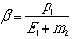と判る。またγは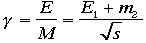とわかります。Lorentz 不変量sの平方根=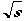がエネルギーの総和です。
重心系の運動量p*は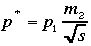となることを確かめてください。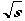を＝E_CMと書く事があります。

粒子１（粒子１に乗った座標系）からみた粒子2の運動について
4元ベクトルp1,p2について以下の量は Lorentz不変である。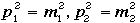さらに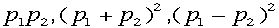これら３つもLorentz不変です。ことなる座標系間の議論をするときは これらの不変量が大切になります。粒子１（粒子１に乗った座標系）からみた粒子2のエネルギーを計算します。これを　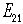と書きましょう。つまり１から見た２のエネルギーと言う意味です。４元ベク トルp1p2の積は次のように計算されます。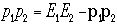右辺のp1,p2は３ 元の通常の運動量ベクトルです。１の系から見ていますから、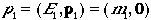です。 よって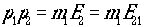ですから、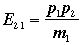であることが判ります。この式の右辺はLorentz不変ですからこの式が 一般の式であることがわかります。さらに1からみた２ の運動量の大きさは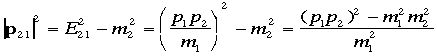とわかる。また速度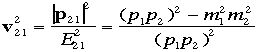と書ける。この速度v21の意味は１から見た１の相対速度ベクトルである。
同じ話しを重心系からみてみる。そこでは仮想的に作られる粒子質量M、4元運動量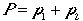（4元ベクトル同士の和である）でうまく書ける。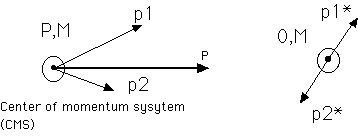重心系からみてはかられる量にはアスタリスク (*)を付けて区別するとして、先ほどのLorentz変換不変性のある式を使って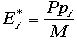となる、なぜなら重心系からみるため、実験室系野木論で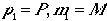と置きかえて良い。また重心系からみた３元運動量の大きさは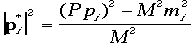という式に置き換えられる。速度も同様の置きかえにより、　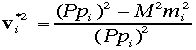一方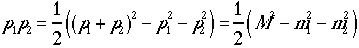であり、また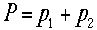であるから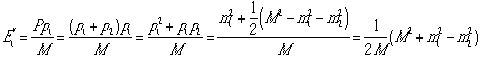
同様に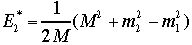、後も同じ置きかえを実行して、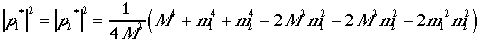
最後に重心系でみた速度は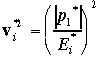と現される。
例題：質量Mの粒子がm1とm2の二つの粒子に崩壊するとき、粒子１からみた粒子２の運動量とエネルギーを計算せよ。


例題：実験室系で入射粒子のエネルギーが10TeV（宇宙線のようなばあい）と同等の能力sをもつ衝突型加速器を作るにはそのビームエネルギーはいくらと なるか？
同様に地球の赤道上の加速磁場をおき地球規模の加速器を作ったとしよう、この加速器ビームエネルギーは磁場が10Tのときどうなるか、またこれを衝突型加 速器で実現するには半径はいくらになるか？ここで相対論的に不変は磁場と運動量の大きさの関係の式を挙げておく。いずれ計算して示す。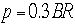ここで運動量p[GeV/c],磁場B[Tesla],半径R[m]であ る。

重心系と実験室系の問題で興味深いのは新粒子の生成問題でしょう。これは質量　Mの粒子を生成するために必要な加速器を作りなさいと言うものです。もしこ れを実験室系でみる型の加速器の場合と実験室系で見る型の加速器では大きさはどうなるでしょうか？


運動の方程式（ニュートンの式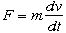）を相対論的にするときは、質量mが相対論では不変ではないし、Lorentz変換のもとでの変換性が 宜しくないので、４元ベクトルを使う。例えば４元速度（γを取り込んで変換性の正しいものを作れる）、や上で述べた運動量とエネルギーの組みである４元運 動量をもちいる。すなわち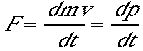が基本式として始める。２体の衝突では全 運動量はその和で定義でき、外力が働かないときは力は無いので、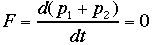が 成立する。
これを重心系に当てはめると当然であるが、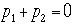であり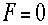が成り立つことがわかる。実験室系では、


Lorentz 変換(Transformation)
3次元空間内の二点間の距離Dは次のように書ける。ただし二点の座標を点１　(x1,y1,z1)と点２ (x2,y2,z2)として（この系の名前をKとしよう）
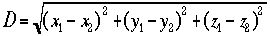　と書ける。またこの二点間の距離Dは光を使って調べることができ る。ここで相対性理論の要請である、「光速度不変」を用いる。これは光速度はいかなる慣性系座表系から計っても一定でc=3x10⁸ (m/s) であると言うものである。慣性座標系とはお互いに等速直線運動をしている座標系同士をいう。点１と点２の時刻をt1,t2とすると、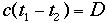と書ける。従って両式をつなぐと、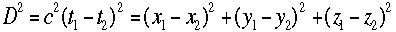が成立する。この二点を別の慣性座標系からながめてその座標を (x1',y1',z1') と(x2',y2',z2')と見えるとき、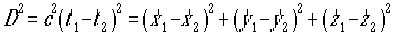
という式が成り立つ。ここでcはダッシュの有る系（Ｋ’と呼ぼう） でも無い系でも同じcで有ることに注意。なぜなら光速度不変だから。
x1-x2などを小さな量（つまり隣同士の位置に移動する）として扱う。こういうときは（x1-x2)=dxと書く。こうして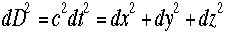であり、ダッシュ系（Ｋ’）では次のようになる。　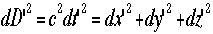さらに移項して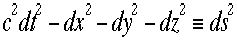右辺のdsはここで定義した新しいほぼゼロの値である。これをダッシュ系 （Ｋ’）も書き下す。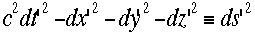
相対性理論の要請その２はどの慣性系から見ても物理法則は同一である。これをKとK'に焼き直して距離を測るとD=D',ds=ds'=0で有ることが要 請その２である。当然ds=ds'が予想される。つまり慣性系に関わらず、この量dsやds'のような形式の量は不変である（ようだ、証明ではないが Lorentz不変量はこうして定義されると良さそうである）
Lorentz変換を考えるときこの不変量の存在は重要である。さてそのLorentz変換はどう書くべきか？であるが、時間を含めた四次元の空間の距離 をdsで定義したことになるので、この量が不変で長さを変えない変換は回転する事である。三次元空間では長さは変わらず座標値が変わる典型例は空間内の回 転であった。従ってここでも四次元空間中の回転を考えれば答えであろう。ｚ軸周りの回転（角度q）は次のように書けた事を思い出してほしい。　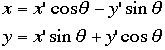　　　　　ここには書いてないがz=z'である。　これと同様にしかし、 ４次元目を含む回転角度αを考える。それはつぎのように書ける。ただしここでちょっとイヤなことがある。それは時間軸tと　空間軸x,y,zのdsへの効 き方の符号が異なることである。そこで空間座標x,y,z と時間座標を同じに扱うような形式を導入しておく。これをτとする。T＝ict と定義する。こうするとdsは次のように書けて、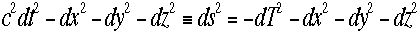dx,dy,dz とdTの符号が一致し扱いやすくなる。そこで回転の式も空間と同じつもりで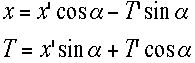　　と書ける。またまた　ｙ＝ｙ’、ｚ＝ｚ’である。これは一般的なｘ−T 平面内の回転であるので、これの意味するところはyやz座標は回転しない、つまりy,z 方向には運動してないと言うことです。これを絵で示すと、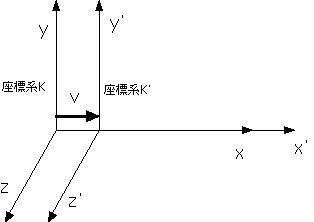というイメージになる。す。つまりK系からみてK'系はx軸の正の方向に速 さvで進んでいる。K'系のx軸x'はxと平行である。とすると、上のαと速さvの関係が解ります。つまり、K'系の座標原点であるx'=0の点はK系か らみて速度vで進む。これ(x'=0) を式に入れると、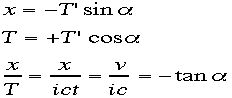
となります。このtanαをiβと置きます。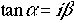
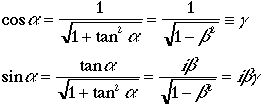ここではγも定義しました。これを使うとLorentz 変換といわれる式が出てきます。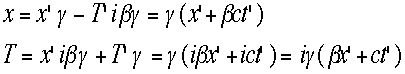

時間の関数Tは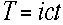より、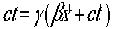 となる。これがLorentz変換の式である。

さてこれをつかわんてはないので、遊んでみよう。もともとの式に戻れるかまず検証します。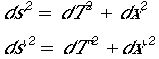でした。dsは不変量であると述べました。このLorentz変換の元で その量が変化しないことをLorentz不変であると言います。つまりdsはLorentz不変だと言い切ったのですがこれを示してください。簡単な計算 でds=ds'で有ることを示すことができます。このことは元々初めから不変であるとして議論を進めて来たわけですが、話しに矛盾が無いことを示したいま す。
もう一つ、非相対論的極限の話しをします。これはLorentz変換でβ=v/cの価が小さい時、つまりニュートンやガリレオの時代の力学の世界に一致す ることを示します。すなわち、　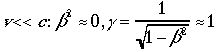　のとき、Lorentz変換は　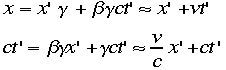　この式はガリレオ変換として知られているものですが、x=x'+ vt'　で等速直線運動（速さｖ）の物体の位置の式（右辺）とその物体に乗った系での位置の関係を表していますね。下側の式はv/c²小 さいのでt=t'と言う式になります。通常の考えです。でも　v/c²が小さくない場合つまり相対論的な場合通常のt=t'は（つ まり世界のどこでも時間の進みは同じだ！という思いこみ）は通用しなくなります。
ここで４元ベクトルを導入します。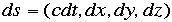と書いて４つの成分をもつベク トルを作ります。この四次元での微少長さds²を次のように定義すると不変であることを述べました。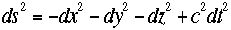従って同じように定義する次の量も同じ変換性を持ちます。
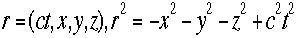さらに普通の意味とは異なる定義で四元速度を定義します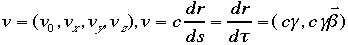ちょっと妙な定義ですが、変換性はよろしく、非相対論近似(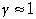)で三元の通常の速度と一致します。第ゼロ成分はc光速となり意味を持ち ません。その意味で４元速度はあまり使用されません。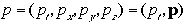これを四元 運動量（あるいはエネルギー・運動量ベクトル）と呼びます。この四元運動量の中身は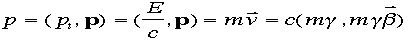ここで、太字のpは三元運動量を示し、βに ついた矢印はやはり三元速度を光速ｃで割ったものを表す。　二乗は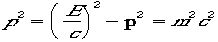こ のように書けて 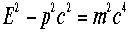という式です。静止質量ｍがLorentz不変なはずですから。

Lorentzー四元ベクトル同士の内積を二乗に似せて作ることが出きる。そしてその内積もやはりLorentz不変である。あるいは内積が一般的で、二 乗はその特別な場合ともいえる。
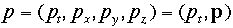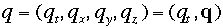
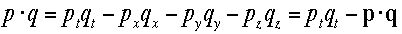,最後の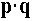は通常のベクトル（３次元）の内積を表し、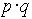は拡張された４次元もベクトルの内積を表します。この量はLorentz 不変な量です。

４元運動量による重心系と実験室系の変換は一般には４ｘ４の行列で表されます。前に述べたように４次元空間内の回転ですから。しかし、Lorentz変換 は慣性系同士の変換である、通常慣性系同士を同じ軸の方向に互いに平行に走らせその相対速度をvとして用います。ここでもいままでx軸方向に互い動く系を 考えて来ました。このとき　y=y',z=z'ですから変換行列の　yとzの関する項は対角成分のみとなり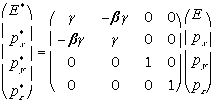ます。まじめに書くとこうなりますが、ゼロをたくさん書くのはかっこ悪ので、初 めの２成分だけ抜き出してしまいます。残りのpy,pzはそのまま動きませんから、忘れます。