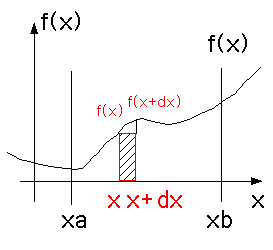物理を題材にしたFortran 入門-2　　　　竹下徹

物理を題材にしたいが、まだ練習問題です。いままでdo ...enddoでloopを回すことを学びました。計算機の最も得意とすることで何回でも計算をさせることができます。人間だとくたびれてやめてしまい たい時だって、計算機は黙々と計算してくれます。また工夫次第で和を取ることも上手にできることを示しました。無限級数和も無限回は不可能としても充分大 きな回数loopを回せば近似的に取ることもできました。

積分

さて次は積分をやらせてみましょう。といっても任意の関数f(x)の積分がで きるわけではありません。計算機でできるのは数値積分つまり、与えられた関数f(x)に対して有るxaからxbまでの数値を得ることがで来ます。これを数値積分といいます。その原理は、次の図を見てください。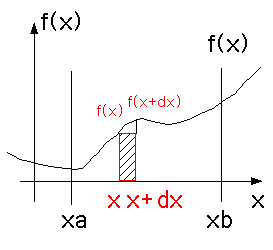f(x)を積分する事はx=xaからxbまでの面積を計算するとこだ！と知っているでしょう。面積は小さな長 方形の部分（図では斜線部）の計算をx=xa,......xbまで続けて行き、和を取れば良さそうに（今のこの図では不足分が明らかに実でますが、横幅 を小さくすれば差は小さくなりそうです）見えます。斜線の長方形の面積は、底辺がdx,高さがf(x)ですからf(x)*dxです、これを次々と和を取り ましょう（前回やりました）！！この方法はとやっていることに相当します。

但し、ｘは等間隔に動かします（プログラムが楽だ）。この方法は長方形公式と呼ばれる方法です。明らかに精度は最悪です。ですからこれを使う人は結 果には要注意です。それでもプログラムはかけます、f(x)=x でxa=0.0, xb=1.0で練習してみましょう。

---------------------------------------------プログラム例

program integral
integer k,kmax
real s,f,x,dx,xa,xb
kmax=100
s=0.0
xa=0.0
xb=1.0
dx=(xb-xa)/kmax
do k=0,kmax-1
x=xa+k*dx
s=s+f(x)*dx
write(*,*) " k and s = ",k,s
enddo
stop
end

function f(x)
real x
f=x
return
end

---------------------------------------------

コンパイルして実行してみてください。今の被積分関数はfunction f(x)に　f=xとかいてありますから、f(x)=xであることが判ると思います。と 手計算できて答えも0.5なのですが、ちょっと違いますね！では積分の巾（長方形の底辺の長さ）を短くして試し手みてください。積分の領域を変えて試して ください。　また　プログラム　で　stop endの後に　function f(x)と　有ります。これはfuction 文といい本体のプログラムをいじらなくても簡単に被積分関数を変えることもできますし、なんと言ってもプログラムが見やすい！ここをx*xとするとｘの２ 乗の積分を実行できます。またsin(x)とするとサイン関数を積分できます。やってみてください。でもやはり積分の精度が悪すぎますね。そこで次のス テップでは台形公式を使います。これは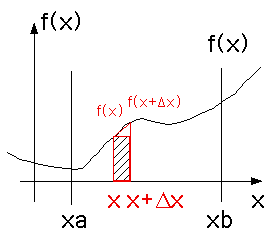図の斜線部分より上の三角も加えて台形で面積を計算しま す。ですからs=s+f(x)*dxをs=s+(f(x)+f(x+dx))/2.0*dx とすればよろしい。注意：端っこでは注意が必要です。つまり、つまり台形で近似したことは高さを平均したことになっています。良い結果が得られましたか？ f(x)が線形だと、台形公式による数値解は、厳密解と同じになります。面積Sはまた次のようにも書かれます。

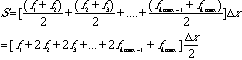さらに上には上があって、Simpson公式と呼ばれます。当然これでは、台形公式 の１次式以上の精度をだすことが可能になります。Simpson公式ではf(x)の一つ手前とその後の３点を２次関数として求めて使います、従って二次曲 線まで数値解は、厳密解と同じになります。 この式の証明は面倒なので、３個の場合にしてみます。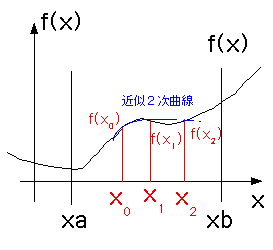

が示されます。全部の和を求めるとを 計算すればよいことになります。

こうやって近似をあげれば積分の計算精度（どのくらい信じて良いのか）は上がって行きます。いつも注意してほしいことは、精度は有限でどこの桁まで 計算が正しいのかは知っていてください。それは例えばdxを変えて結果が変わる稼働か、などテストする必要があります。

微分

次は積分の反対の微分です。といって微分方程式を数値的に解くことができることを示します。つまり数値的に解くというのは有る入力パラメータの数値 は決められた時、微分方程式を差分方程式と見なし追いかけて行き、微分法方程式に従う答え（解）を計算する事を言います。例えば、微分方程式は手でつまり厳密に解くことができます。それでもまあ数値的に計算に解かせてみましょう、というのがこの項の 目的です。dtというのは時間の微分を表す極限値ですが、有限微少量に戻します。そもそも微分はな ので、一番右と左をつなげて、とかくことができます。つまりこの式の左辺は時刻がt からdeltaだけ進んだx(t+delta)であり、右辺は時刻ｔでの速さ(=dx/dt)とx(t)で 表されています。時刻tでの位置と速さが判ればそこから時刻がdeltaだけ進んだ時の位置は計算できるという式に読み直すのです。この式を差分方程式と 呼びます。2階の微分はどうやるかって？？？同様にですから、両者の差をdelta で割れば2階微分がでます。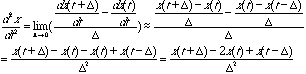さて自由落下の問題の運動方程式は２階の微分方程式な ので、１階づつ順に解く方法でやってみましょう。なので、とすればよろしい。また位置x(t)はを 使います。これをプログラムにして書いてみると。

-----------------------------------自由落下の運動プログラム
program fall
c fall in one dimnesion is silmulated
integer i
real g,dt,t,x0,x1,v0,v1
parameter(g=9.8,dt=0.01)
c mass=1 equivallent
t=0.0
x=0.0
v=0.0

do i=1,1000
t=t+dt
v=v-g*dt
x=x+dt*v
if(i .eq. i/10*10) then
write(*,*) t,v,x
endif

enddo
stop
end

-------------------------------------

ここではv=v-g*dt のようにv(t+dt)左辺  とv(t)右辺を同じ変数でつないでいます。　右辺はまだこのdo-loopの中での値であり、もう一回do-loopが回ってくるとき、左 辺の値が今度は右辺に使われるという仕組みです。これでt+dt とｔの区別をあからさまにする必要が無くなります。

このプログラムを例えば、fall.f と名付けて保存してください。ここで、　　.f を付けたのはコンパイラーg77にfortranプログラムであることを知らせるためです。さてこれをg77 fall.fとしてコンパイルしましょう。コンパイルの結果できた実行形式のファイルは a.outです。これを ./a.aoutとして実行すると、百行次のような出力が画面にづうううらああと出てくるはずです。

所でこのプログラムではif( ) then .... endifが初めて出てきました。これif()のかっこ内が正しい場合then以下のwrite 文が実行されます。そうでない場合はここでは何もせず終わります。このように判断をするのがif文です。ここではi が i/10*10に等しく（.eq.）なるとthen からendifが実行されます。このように判断をするために、 .gt. (>) とか .lt.（＜）等があります。

.............

9.92013168 -97.2156143 -481.703339
9.93013191 -97.3136139 -482.675507
9.94013214 -97.4116135 -483.648651
9.95013237 -97.509613 -484.622772
9.9601326 -97.6076126 -485.59787
9.97013283 -97.7056122 -486.573944
9.98013306 -97.8036118 -487.550995
9.99013329 -97.9016113 -488.529022
10.0001335 -97.9996109 -489.508026

縦の列　一番左は　時間です空白を一つおいて、次が速さ、また空白を一つおいて最後が位置です、gは9.8にとってあるので、プルグラムはMKS単 位系で書いてあると読めますから、質量m=1kgの（といってもここでは結果は質量に無関係です）場合の速さ（上向きを正の軸に取った）と位置（上向きを 正の軸に取った）を計算させました。位置は原点x=0から初速度v0=0.0で出発したので、自由落下を表しています。x(t)=gt**2/2 になっているのが判りますか？判りませんよね。個言うときはグラフを描かせましょう。そのためにはgnuplotを使います。おっとその前にプロットさせ るデータを準備する必要があります。そのため redirectionという　UNIXの　便利ツールを使います。　./a.out とやって出力ががさーと画面に出るのではなくファイルにその内容を落とす事を　 ./a.out > fall.d とかやってください。画面には何も出ず、実はファイルができています。名前はfall.dと付けました。.d　はデータということを示すつもりです。　こ れの中身は more fall.d　としてみてください。　数値がずらーーと並んでいるはずです。さてgnuplotです。コマンドラインからgnuplotと打つとなにやら ごそごそ言ってきて最後にgnuplot>と書いてカーソルが点滅始めます。ここからはgnuplotの世界だよ。と言ってます。gnuplotの 使い方やマニュアルは五万とインターネットに転がってますから自分で役に立つ性にあるものを見つけてbookmarkに入れておきましょう。そこで　 plot "fall.d"とやってみましょう。こ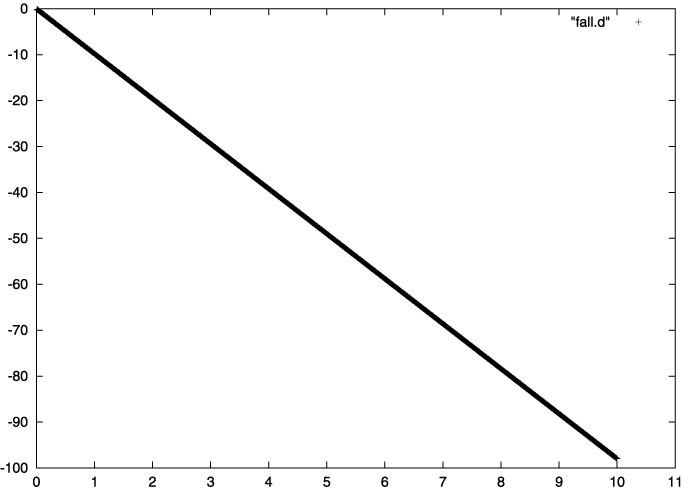んな図が出てきますね。これは横軸にデータファイルの １番目の数値（つまり　時刻　t )、縦軸にデータファイルの2番目の数値（つまり　速度　v )をプロットしたものです。厳密解はv(t)=-gtですから直線になります。但しこの図は直線を描いたものではなく、点（実は　×点）の集まりです。さ て plot "fall.d" using 1:3とすると次の図が出てきます。これは横軸にデータファイルの１番目の数値（つまり　時刻　t )、縦軸にデータファイルの3番目の数値（つまり　位置　x )をプロットしたものです。厳密解はx(t)=-gt**2/2ですから二次曲線になります。但しこの図は直線を描いたものではなく、やはり点（実は　× 点）の集まりです。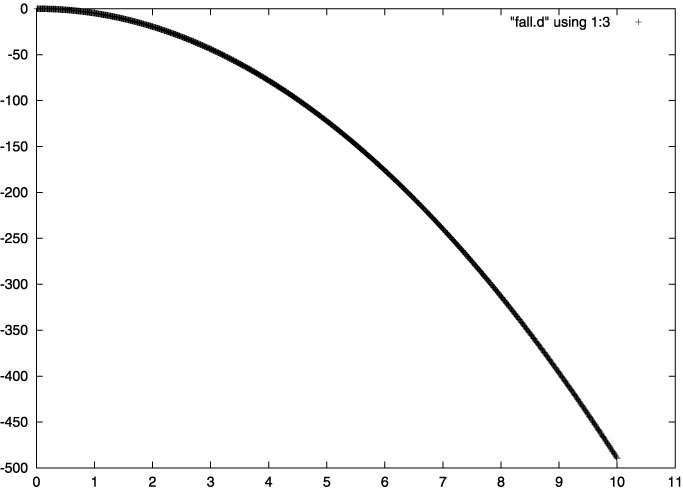

さてこれからが本番です。微分方程式の中に空気抵抗力が入っていると、運動方程式は次のようになります。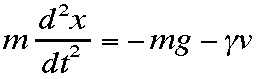ここで右辺最後の項が速度に比例する空気抵抗力を表し、その係数をガンマーγとしています。マイナスがつくの は、判りますね、抵抗だからです。進行方向と逆に働く抵抗力はいつも進行方向に関係するvベクトルにマイナスがつきます。この方程式も厳密にとくことがで きますが、ここでは差分方程式にして数値的に解きましょう。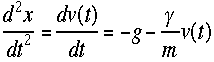プログラムではを次のように書き直せばよい。v=v-g*dt-gam/mass*v*dt, x=x+dt*v ここでgamはγの空気抵抗係数です。この変更でコンパイルして動かしてみてください。

9.90013123 -61.6035461 -354.164917
9.91013145 -61.6399422 -354.780945
9.92013168 -61.6763039 -355.397339
9.93013191 -61.7126274 -356.014099
9.94013214 -61.7489166 -356.631226
9.95013237 -61.7851677 -357.248718
9.9601326 -61.8213844 -357.866577
9.97013283 -61.857563 -358.484802
9.98013306 -61.8937073 -359.103363
9.99013329 -61.9298134 -359.72229
10.0001335 -61.9658852 -360.341583　　こんな出力がでますね。ここで注目してほしいのは最後の行でつまり、１０秒後の速度と位置です、それぞれ-62m/sと- 360mです。これを上の方に書いた空気抵抗のない場合の速度(-98m/s) と位置 (-490m)と比べてください。空気抵抗の効果がはっきり判りますね。速さの絶対値は小さくなっています。当然です、飛ぶのをじゃまするのが空気抵抗で すから。また飛距離も小さくなっています。このデータをまたまたredirectionして　ファイルに落とし、gnuplotでみてやりましょう。. /a.out > fallinair1.d 等とやります。　ちなみに gnuplot > plot " fallinair1.d" で時間と速度をプロットしてやることができますが、絵として絵を保存するには、　　plot するまえに gnuplot> set term postscript とまずやって、 つぎに　gnuplot> set output "fallinair1.ps"　とやってから　ポストスクリプト形式の絵の出力フォーマットを決め、ファイル名も決め手やります。その後　 gnuplot>plot "fallinair1.d" 　とデータファイルをプロットしますが、画面は変わりません。出力が変更されたので変化しません。その出力ファイルをみたいときは　コマンドライン（つま りgnuplot の外）から　gv fallinair1.psとやってみてください。gvというなのソフトで .ps つまりpostscriptファイルを画面に見せてくれます。 gv はghostview　の略です。それをここに載せます。但し、ファイルフォーマットをjpegに変換しました。

ところで、結果は横軸が時間で１０秒まで、縦軸速度です。これではまだ不十分ですね、まだ終端速度に達していません。みなさんはプログラムをどう変 更すれば良いか判りますね。次のような絵を出してください。

やっとそれらしく終端速度が見えてきました。グラフから読みとるとおおよそ100m/sのようです。これは微分方程式から得られる値　- g/gam*mass=-9.8/0.1*1.0=98m/sとほぼ等しいので納得できる。またx-t関係、横軸時間で縦軸位置では、

終端速度付近の時間 （ｔ＞２５ｓ）で直線が見えます。これは等速度運動なのでxはtに比例するが見えています。

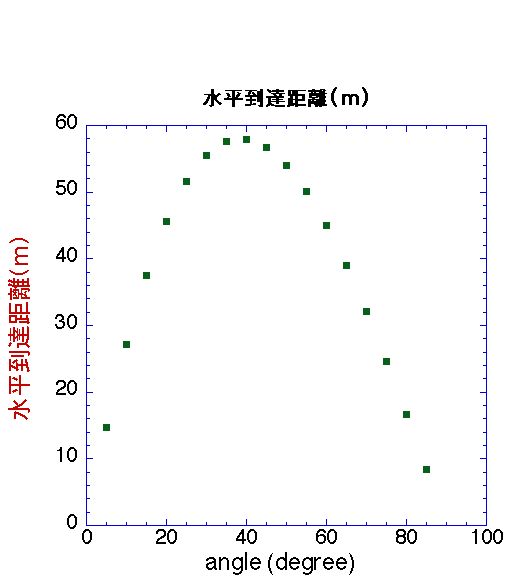
では問題です。通常空気抵抗のない放物線を描く２次元の投げあげ問題では４５度に投げあげると最大距離到達しますが、空気抵抗が有る場合はどうなる でしょうか？

まず２次元の投げあげですから、２つの次元の変数をそれぞれ用意する必要があります。それを　x,vx とy,vy ここでは変数yを鉛直上向きに取りましょう。水平方向がxです。

vx=vx-k*vx*dt
vy=vy-g*dt-k*vy*dt
と空気抵抗係数はxにもyにも同じ形で入れましょう。下の図はk=0.2,初速度30m/sで６０で上向きに発射したときの、x-y平面ないでの飛跡で す。角度を変えて試したみてください。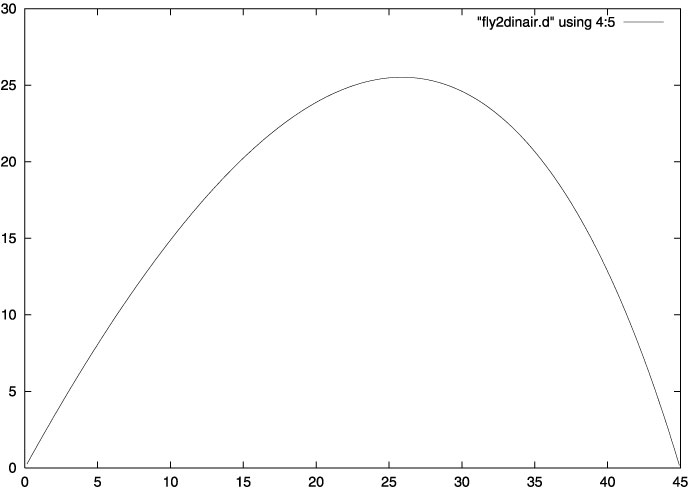

角度を変えて計算するプログラムにしました。

do 20 j=1,17 <<<<<<このdo-loopが角度について回っています。5度から85度まで17個
theta=j*5.0　　　　　　　　角度の度での計算
thetarad=theta/180.*pai　　＜＜＜＜角度をradianに直す
t=0.0
v0=30.0　　　　　　＜＜＜初速度　30m/s
x0=0.0 　　　　　　＜＜＜初期位置　　ｘ
y0=0.0　　　　　　＜＜＜初期位置　　ｙ
vx0=v0*cos(thetarad)　　　＜＜＜初速度　ｘ方向
vy0=v0*sin(thetarad)　　　＜＜＜初速度　ｙ方向

do 10 i=1,3000　　　　　　　＜＜＜微分方程式を解くloop
t=t+dt......

.....................

if(y1<0.0) then 　　　　　　　　　　　<<<最終的な結果のみ打ち出すためのif
write(*,*) v0,theta,t,vx,vy,x,y <<<最終到達地点
goto 20　　　　　　　　　　＜＜＜もう用はないので、次の角度へすすむ。
endif

...............

10 continue

20 continue

stop　　これによると40度よりちょっぴり小さいかな？というところでしょうか？空気抵抗係数によりこの値は変わります。

もう一つおもしろい問題があります。それは空気抵抗が速度の２乗に比例する場合です。

単振動も計算できそうですね、　(dv/dt)=(加速度）=-(k/m)x ですから。

(加速度)=(dv/dt) = lim (v(t+dt)-v(t))/dt が定義ですが、微分ではなく差分として (加速度)=(dv/dt) = (v(t+dt)-v(t))/dt　　としてしまいますね。そうすると、　v(t+dt) = v(t) + (加速度)*dt　、位置情報　ｘについてもどうように　　(速度)=(dx/dt) = lim (x(t+dt)-x(t))/dt が定義ですが、微分ではなく差分として (速度)=(dx/dt) = (x(t+dt)-x(t))/dt　　としてしまいますね。そうすると、　x(t+dt) = x(t) + (速度)*dt という計算式で　時刻t の速度 v(t) と位置 x(t) から　時刻t+dtの速度 v(t+dt) と位置 x(t+dt) を左辺として計算できることがわかります。　単振動では　　(加速度) = (dv/dt ) = -(k/m) *x であたえられるので、差分方程式を逐次的に数値として解くことができます。この解は単なるsin (wt) やcos(wt)なので面白くも何ともないので、これに空気抵抗型の力を入れましょう！　(加速度) = (dv/dt ) = -(k/m) *x - b/m * v とすればやはり解くことができそうです。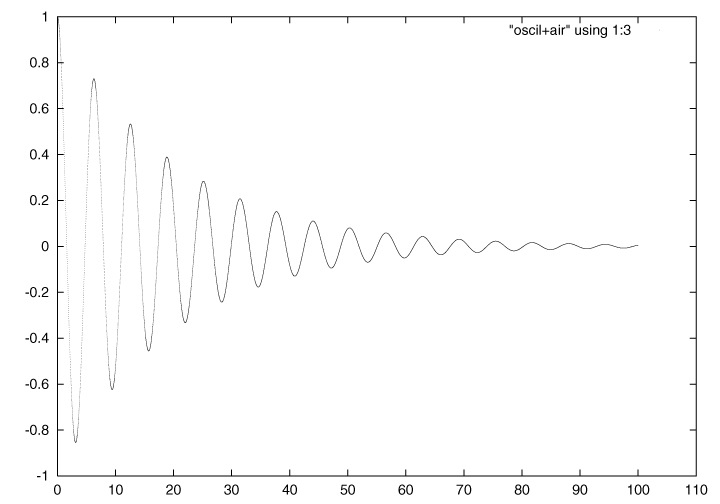 と次のような１年生のとき力学で解いた減衰振動をみることができます。

惑星の運動も計算できそうですね、　(dv/dt)=(加速度）=-(GM) /r**2 ですから。

太陽系のような万有引力の元の運動では　　(加速度) = (dv/dt ) = -(GM) /r**2 であたえられるので、差分方程式を逐次的に数値として解くことができます。この解は初速度により三種類に分類されます。即ち、（１）初速度が不足して太陽 に落ち込む場合、（２）束縛されて周期運動をする（円あるいは一般にはだ円軌道を画く）、（３）初速度が大きすぎて、引力圏から脱出する場合（軌道は放物 線か双曲線となります）。

重力定数G=1.0,MSUN=1.0 で解かせてみます（現実には存在し得ない価ですが）。初期値はx=1.0,y=0.0から出発します

初速度がvx=0.0,vy=0.6のとき。　だ円軌道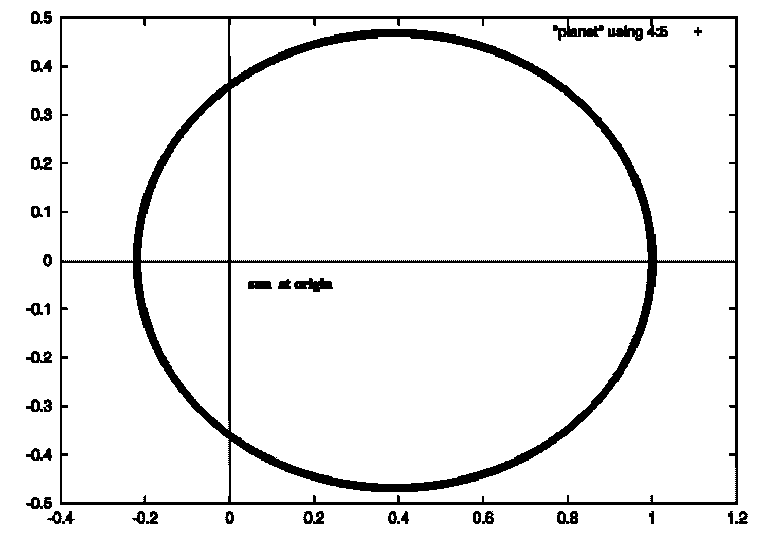　

初速度がvx=0.0,vy=2.0のとき。　双曲軌道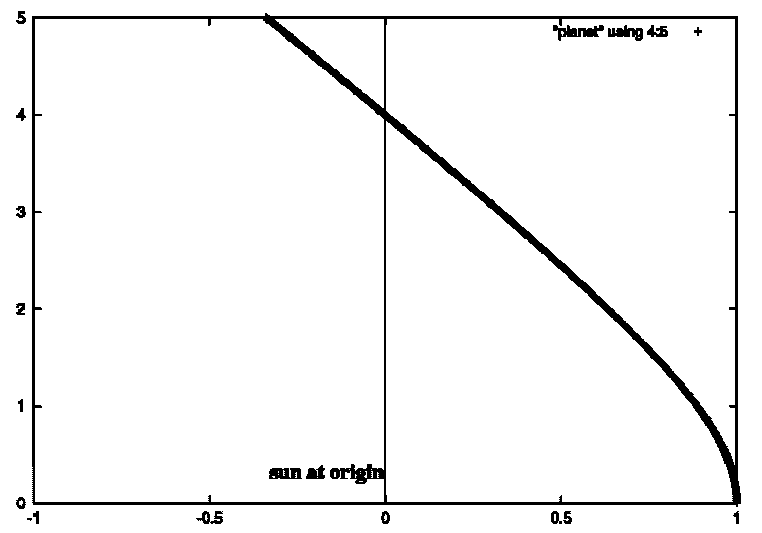　　

つぎは配列のお勉強です。

　配列は物理の言葉では　ベクトル　あるいは　行列に　対応します。　実数あるいは整数型の変数名のあとに( )がつきます。例えばVx,Vy,Vz を V1,V2,V3 と書いてさらにカッコを付けて、V(1),V(2),V(3)と対応付けます。　さていくつか実数型のデータ 　data()がある時、これの平均を取るプログラムを作りました。

program takemean
integer i,nmax
real mean,data(10)　　＜＜＜配列の定義
mean=0.0
nmax=3
data(1)=3.4　　　　　　＜＜＜実数の代入
data(2)=2.6
data(3)=5.5

c do i=1,nmax
c read(*,*) data(i)

c enddo
do i=1,nmax
mean=mean+data(i)　　　＜＜＜和を取る
enddo
mean=mean/nmax　　　＜＜＜最後に平均値とする
write(*,"(f10.2)") mean　　　＜＜＜精度を考え印刷する
stop
end

とこういうものです　問題の配列(英語ではarray)は 3行目にreal data(10)と切られています。そのうえデータを３個入力しました。入力をここでは代入で行っています。次にdo文で全ての和を計算し、その後個数で 割って平均値を計算しています。 いま　入力データは　3.4と2.6と5.5ですが、これをキーボードから入力できるように改造するのが中断のコメント文です。この先頭の c をとってコンパイルして実行してみてください。計算機は入力待ち状態にはいりキーボードから入力しない限りなにもしません。この場合３個データをキーボー ドから入力すると平均値を計算します。さらにデータファイルを次に様に準備してみましょう。

と左上から一行に一つづつデータが並んだファイルをdataとして作り保存します。これを ./a.out < data

として実行すると、同じ結果を得ます。このようにキーボードからの入力をredirectionして　ファイルから入力をすることが可能になりま す。　　実験データの整理などに便利でしょう。