物理を題材にしたFortran 入門-3　　　　竹下徹

物理を題材にしたいが、まだ練習問題です。いままでdo ...enddoでloopを回すことを学びました。ここではif() then ... endif  というif文を学びます。条件があるとき、これに従いやることを変える事ができます。

 IF 文

if文は一般に次の形式を取ります。
if(  A  )  then
B
else
C
endif
この３行でAが正しい、つまり成立するとき Bを実行し、そうでないとき Cを実行します。
例えば real x ,y  に対して
if(x>0.) then
   y=x
else
   y=-x
endif
  とすると実数型の変数　x　の絶対値を取った値を　yとしていることがわかりますね。
もう少し複雑な書き方として 
if(  A.and.B  )  then
C
else
D
endif
とういうのもあります。これは論理計算　A and B ( AもB も両方とも正しい時）Ｃを実行し、そうでないとき、（つまり　Aは正しいがBが正しくない時、Aは正しくないがBが正しい時、Aは正しくなく、Bも正しく ない時）Ｄを実行するものです。このような　A,Bは論理変数と呼ばれる定義　が必要です。
 logical A,B　　としましょう。

さて
今回の課題として，コンデンサーの周りの静電ポテンシャルを計算することに挑戦してみましょう．ただし境界条件が決まっていないと問題は解けませんから， 箱の周りは全てアースされていて電位つまりポテンシャル＝０，箱の中のコンデンサーの上側の板の電位を10，下側の電位を-10とします．このとき箱のな かの電位はどうなるだろうかというのが課題です．

電荷のないところでの電場Eはマックスウェルの方程式の電荷密度ゼロの式
div(E)=0
に従います．電場EとポテンシャルVの関係は
E=-grad(V)
ですから，
laplacian(V)=0
が解くべき方程式となります．これを具体的に書き下すと，２次元の配列V(x,y)に対して、
d2V(x,y)/dx2+d2V(x,y)/dy2=0　
この方程式はラプラス方程式とよばれ，電磁気に限らずなぜか至る所にあらわれます．

さて計算機を使った数値計算では，微分を直接解くことはできませんから，差分で置き換えます．すなわち，xの関数f（x）の微分df/dxは，小さな量 deltaを使って
{f(x+delta)-f(x)}/delta
と近似されます．
２次元の関数V(x,y)の場合も同様に，
dV(x,y)/dx={V(x+delta,y)-V(x,y)}/delta,
dV(x,y)/dx={V(x-delta,y)-V(x,y)}/delta,
２階の微分係数は１階の微分のもう１回の微分ですから，両者の差を取って，
d2V/dx2={dV(x,y)/dx-dV(x,y)/dx}/delta
={V(x+delta,y)-2V(x,y)+V(x-delta)}/delta2
y微分も同様に行い，結局ラプラス方程式の差分方程式は，
V(x+delta,y)-2V(x,y)+V(x-delta,y)+V(x,y+delta)-2V(x,y)+V(x,y-delta)=0
あるいはちょっと書き直して，
V(x,y)={V(x+delta,y)+V(x-delta,y)+V(x,y+delta)+V(x,y-delta)}/4
ラプラス方程式は，ある点の場の価Vは周りの上下左右４点の場の平均だと言っているのか！と感心してみてください．それでいろいろなところにラプラス方程 式が顔をだすはずです．

さて，いよいよコンデンサーの周りの電位V(x,y)を求めてみましょう．適当な電位から出発して，ラプラス方程式の差分式をときながら，つまりV(x, y) を左右上下の価の平均値に置き換えて行きます．ただし，境界条件である，箱の部分とコンデンサーの電極の電位はそれぞれ一定に保っておきます．一度だけで はだめで，何度も繰り替えしを行うとだんだん望ましい調和のとれた配置の値に近付いて行くだろうと期待します．次にプログラムの例を示します．これもスタ イルや変数の置き方の例であり，皆さんは皆さんのスタイルでプログラムを書いて下さい．
さて１０１ｘ１０１のメッシュで区切られた２次元空間に電位+5Vと-5Vの板（コンデンサーを作る）を
図のように置きます。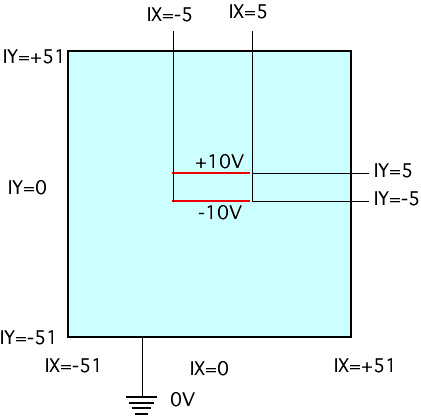

---------------------------------------------プログラム例
      PROGRAM condf
      real V(-51:51,-51:51)
      logical LX, LY1, LY2

      do 10 IY = -51,51      !   V(x,y)をゼロにしておく
      do 10 IX = -51,51
   10 V(IX,IY) = 0.0
     
      do 1000 N=1,200       !  回数のループ

      do 100 IX=-50,50         !  x方向のループ　　端は計算しない、いつもゼロ電位だから

      LX=IX.GE.(-10) .and. IX.LE.10

      DO 200 IY=-50,50       ! y方向のループ　　端は計算しない、いつもゼロ電位だから

      LY1=IY.eq.(+5)
      LY2=IY.eq.(-5)

      if(LX.and.LY1) then         !  condensor上の電位はいつも一定  if文です。
        V(IX,IY) = +10.0
        goto 200
      endif

      if (LX.AND.LY2) then        !  condensor上の電位はいつも一定
        V(IX,IY) = -10.0
        goto 200
      endif

      VL = V(IX-1,IY)
      VR = V(IX+1,IY)
      VU = V(IX  ,IY+1)
      VD = V(IX  ,IY-1)

      V(IX,IY) = (VL+VR+VU+VD) /4.0   !　ここで周りの場　Ｖの平均を取る。これがラプラス方程式の極意
  200 continue
  100 continue
 1000 continue
 
c      do 5000 IY=０,0
c         write(*,300) (v(ix,iy),ix=50,-50,-1)
c 5000 continue

        iy=0
        do ix=-51,51
            write(*,*) v(ix,iy)
        enddo

 300  format(21F6.2)
      stop
      end
-----------------------------------------------------------
このプログラム例では，ポテンシャルV(x,y)をひとつしか用意していないので，ラプラス方程式を利用して新しいV(x,y)を計算して格子点(x, y)をめぐってゆくとき，Vがどんどん置き換わって行きます．

最初のfor文で周囲の箱の電位を含めたすべての点の電位V(x,y)をv[i][j]=0.0として初期化していますが，皆さんはこの値をかえて任意の 場Vから出発しても同じ結果にたどり着くことを確かめて下さい．またコンデンサーの電位を変化させて場がどのような形に変化するかも計算させてみて下さ い．

。