物理を題 材にしたFortran 入門-4　　　　竹下徹

物理を題材に、シミュレーションを行います。その始めは乱数です、こ れにヒストグラムを使って解析します。乱数は自然界のランダム性に支配される現象を計算機で再現しようとするとき、特によく使われる道具です。ランダム性 とは、自然ですら制御できない、ましてや人間の制御の利かない、いわばサイコロを振って次の行き先を決めているような性質で、自然界の根本部分に関わって います。

乱数

普通一様乱数のことで、その名の示すとおり「乱れた；みだれた」数で す。乱れたという意味は、何の規則性もなく乱れたということで、ある数が作られ次の数を予言できないほどでたらめだという意味です。しかし実は計算機では 全く規則のない乱数は造れません。つまり順番は同じだが、発生された（作られた）数つまり、乱数としては十分に乱れている数の列を作り出すことができま す。これを計算機乱数、あるいは疑似乱数とよびます。疑似とついているのは、順番に関してはある種の規則性があるので、完全な乱数ではないという意味で す。計算機乱数では呼び出す度に異なる（疑似でたらめな）値を返す程度に理解して下さい。計算機により作られた乱数の列はいつかは同じ値を取ります。この 後は同じ繰り返しとなります。繰り返しまでの回数が充分にお大きければ実用上、「真の乱数」とみなすことができます。

良く知られた線形合同法による疑似乱数の生成プログラムといものも存 在しますが、ここではこれを外部関数として利用します。関数名はrand(0)です。

c test program for rand(0) to generate random number
program randt
real r
do i=1,10
r=rand(0)
write(*,*) r
enddo
stop
end

このプログラムをコンパイルして実行すると

0.840187728
0.394382924
0.783099234
0.798440039
0.911647379
0.19755137
0.335222751
0.768229604
0.277774721
0.553969979

こういう結果が画面に表示されます。　　write文で実数変数ｒを 10個印刷したのから10行見えてます。察するにこのrand(0)は０から１．０の間の乱数を生成するようですね。最大値は１．０かどうか調べてみてく ださい。そのためには最大値をrmaxと例えば定義して、do-loop[の中でif(r>rmax) then rmax=r endifとかすると、生成された乱数rが今までの最大値rmaxを越えると置き換わります。これを何回かdo-loopを回して繰り返して、その後に印 刷を行うとそこまでの最大値を得ることができます。10回乱数を振ってやってみると、ちゃんと 0.911647379が出てきました（なにしろ同じ乱数列を生成するので）。上の１０個の計算結果を目で見ても明らかでしょう？！　実はこの計算は最大 値を探しています。最小値も探してみてください。試しに、最大値は１００万回やると、 0.999998331でした。やはり１．０を越えていないようです。最小値も試してください。ところでこの乱数の列はもう一回実行つまり ./a.outとやると全く同じ結果を出します。つまり乱数はその発生順番を追ってゆくと結構ぐちゃぐちゃの乱数ですが、一回リセットして再実行するとま た同じ乱数の列を作り始めます。さてこの列を変更するにはcall srand(NUM)として１回　do-loop　の前に呼んでください。このcall xxxxというのは　xxxxという名前のsubroutineを呼ぶ作業なのです。srand()の中のNUMは整数で乱数の初期化のための値です。こ の値を変えると生成される乱数列が別なものになります。この値　NUM のことを seed 種と言います。　種を変えて別の乱数列が発生できることを試してください。このように計算機では、シード（種）と呼ばれる初期値に依存した乱数の列を決め て発生させることで動かします。これは計算機で乱数を用いて計算させたとき、結果が違う場合、同じ乱数列で計算結果をチェックするために大変有用です。た だし自然界ではこの様な事は起こりませんから、毎回異なるシードを見つける工夫が必要です。例えば実行時の時刻とか、、、、皆さんも考えて使えるようにプ ログラムを変更してみて下さい。

さてこの乱数はどんな分布をしているのでしょうか？分布？はい、乱数 は毎回作るごとに異なる値をするわけですから、複数個作って「同じくらい」の値がどの程度（頻度）出るのかを知ることが分布という概念です。この「同じく らい」の値は、実数値を問題にする場合原則として毎回異なる乱数値を生成するわけですから、有る程度の巾をもって「同じくらい」と言わなければなりませ ん。これを　bin 巾と呼び、同じbinに入った個数を数えてグラフ化することをヒストグラムを取るといいます。では具体例を示しましょう。0から1までの実数値をbin巾 0.1でhistgramを取ってみましょう。ヒストグラムは、物理の世界では良く利用されるグラフです。同じようなことが何度も繰り返し起こる場合にそ の結果の値を集計して、値が適当に同じ大きさ範囲に入る時その繰り返しの数を縦軸に積み上げて行きます。横軸には値の大きさを取ります。ですから、適当な 大きさの範囲を大きく取りすぎても、小さく取りすぎても意味のないグラフとなります。下のプログラムではヒストグラムのデータはUNIX-likeにファ イルとして読みとります。またヒストグラム化は１０個のビンについて行うように作られています。

integer nb,nmax,ix,i,hist(10)
nb=10
c clear histgram buffer
do i =1, nb
hist(i)=0    　＜＜＜ヒストグラムを初期化してます
enddo
call srand(1247)　　＜＜＜乱数の初期化
do i= 1 , nmax
x=rand(0)　　　　　＜＜＜＜乱数１個発生
ix=nb*x+1　　　　　　＜＜＜ヒストグラムのビンの番号ixの計算
hist(ix)=hist(ix)+1　　　＜＜＜ヒストグラムのビンに一つ加えています
c write(*,*) i,nmax,nb,x,ix
enddo
do i=1,nb
write(*,*) i,hist(i)　　　　　　＜＜＜ヒストグラムの表示
enddo
このプログラムを全体を正しくしてコンパイルして実行すると、

1 9
2 9
3 10
4 11
5 8
6 9
7 6
8 13
9 9
10 16

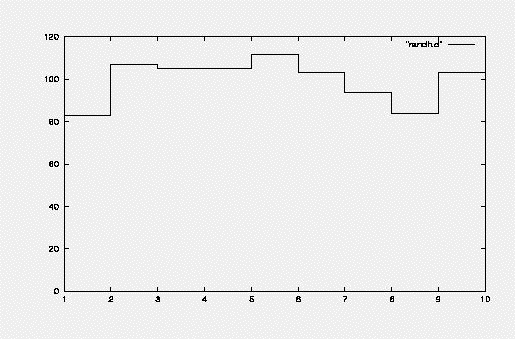
という結果が画面に表示されます。これはhist()という配列中の ｋ番目に入っている個数がhist(k)個であることを、　ｋ　とhist(k) を印刷する事により得ています。 乱数 x=rand(0) を作り、 ix=nb*x+1、実数xに整数nbをかけて（これがビン巾に相当します）、１足してビン番号　ix　を得、 hist(ix)=hist(ix)+1 ヒストグラムバッファーhist()の ix　番目を　１　増やしてやります。ヒストグラムバッファーhist()　は始めはゼロになっています。いまは　１００個の乱数で実行しました。計算機 は自由に回数を増やしても文句を言いませんから、試してください。さてその結果はグラフにしてみましょう。ここでもgnuplotを使います。

gnuplot> set terminal postscript
Terminal type set to 'postscript'
Options are 'landscape noenhanced monochrome dashed defaultplex "Helvetica-Ryumi
n" 14'
gnuplot> set output "randh.ps"

gnuplot> plot [] [0:] "randh.d" w step

と続けて実行すると、今いるあなたのdirecotry中に randh.psというpostscript形式のフォーマットの図のファイルができます。これを確認するには gv randh.ps と実行するとghostviewが立ち上がって図を見せてくれます。それをここへ載せます。〔注：postscript というファイル形式は図形形を同じに保って大きさを自由に変える事ができるように工夫して作られてたファイル形式である。中はascii形式なので読むこ とが（editorなどで）できる。UNIX やMacintoshの世界で普通に利用されている）少々がた がたしていますが、一様分布らしい振る舞いをみることができます。もっと統計をあげて（つまりたくさん乱数を作って同じ図を出してみてください。相対的に がたがた（分散）は小さくなって行きます：これは中心極限定理の教えです。）

さてそれでは一様分布する乱数rand(0)から他の分布をする乱数 列を作ってみましょう。

x=rand(0)
y=acos(2.0*x-1.0)
ix=nb*y/3.14159+1
hist(ix)=hist(ix)+1

これを実行するとxは一様乱数で、2.0*x-1.0 は -1 から +1の間を一様に分布する乱数です。さらにy=acos(2.0*x-1.0) で　acosはcosの逆関数で、yとして0.0から3.14159＝パイの間に分布する（頻度が問題です）乱数列を計算しヒストグラムにします。これを ヒストグラムでみると、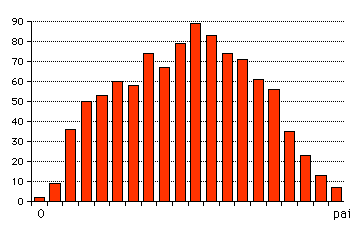と いう形になります。ですから、y はsin型の分布関数をすることになります。どうやらsin()型に分布する乱数を作りたかったら、その逆関数 を用いるらしいことが想像できます。　さて練習問題として、exp()型やcos^2()型の分布をする乱数を作ってみてください。

ガウス関数型の分布をする乱数は別の方法でも作ることができます。こ れには中心極限定理を用います。中心極限定理では「どんな分布をする変数xiに対して、Y=(x1+x2+...+xN)/N で定義される。変数Yjはガウス分布をする」というものです。証明は調べてください。ここでは実際一様分布する変数xiのN個の平均としてのYjの分布を 調べてみましょう。結果は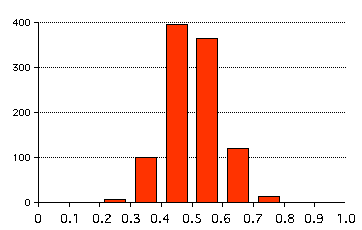こ うなりました。ここではN=12にとり、１０００個のYの分布をヒストグラムしています。そこそこYはガウス分布すると言って良いですね。ヒストグラムが 判りましたか？

さて乱数を使ったおもしろい話しです。

（１）（放射性）原子核の崩壊現象　

一つ一つの原子核はどのタイミングで崩壊するなどなにも考えていません。そりゃそうでしょう！つまりどのタイミングかは、かってだとい うことです。この「かって」を有る時間幅の中（これを単位時間としましょう）で崩壊するか、しないかと判定します、するかしないかは、一様乱数r:   0<r<1 をふってその値がある値p : 0<<p<1より小さいとき崩壊する、そうでないとき崩壊しないとしましょう。pは単位時間当たりの崩壊確率 に相当します。つまり単位時間内の崩壊確率はどの原子核も一定とするのです。あとは多数の原子核を集めてきて、その全体数が時間とともにどのように変化し てゆくのか、を見ればいいでしょう。

横軸は、時間を整数で表したもので単位時間の整数倍を示します。縦軸が最初に１０００個の原子核が有ったとして場合の時間がたったとき の残り原子核数です。縦軸をlogでプロットすると、 gnuplot > set log y と、このようになります。

直線が見えると言うことは、崩壊が指数関数的で有ることを示します。

実は原子核の崩壊が残った数の時間による変化が上の図ですが、単位時間に崩壊した個数の図も出すことができまして、次のようになりま す。ちなみにこれらの絵は１０００個原子核がt=0の存在して、その後崩壊して残った数が上の図で、崩壊した原子核の数が下の絵です。ここで短時間あたり の崩壊確率p=0.1としました。最初の点は約９００個残り、１００個崩壊した点からグラフが始まっています。皆さんはp を変えると崩壊の寿命が変わる事を自分で確かめてください。

（２）　フェルマー  (P.Fermat)の原理をつかって屈折角を出してみましょう。

　　フェルマーの光の原理は「光は最小時間で２点間結ぶ」といいます。このことは、物理現象が実現されるのは、極値（極大または極小） を取るときだ！という例です。極値はの原理は、最小作用の原理で学んだことと同じ概念に見えます。さて媒質１の屈折率をn1, 光の速度をv1, 真空中の光速をｃ、とするとv1=c/n1 です、光が媒質２に入ると同様に関係を満たし、v2=c/n2 の関係が成り立ちます。今次の図のような場合を考えます、

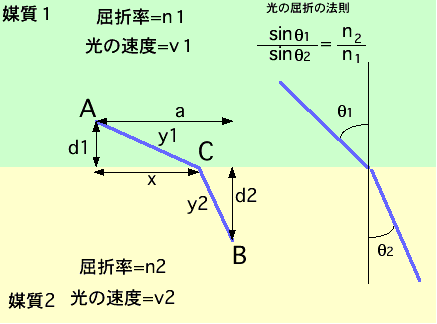
x が約
0.4のところで縦軸（AB間を飛ぶ光の時間）が最小値をとります。このときn1=1.33, n2=1.0 で,d1=d2=1.0した。この経路を光は通とフェルマーの定理は主張します。中学校で覚える公式　sin (thera)1/sin(thera)2=n2/n1 かというと、sin(theta)1=x/y1, sin(theta)2=(a-x)/y2, 

sin (thera)1/sin(thera)2=0.72

n2/n1=1.0/1.33=0.75

ううむちょっと違うが、計算は超微妙なのでよしとしましょう。みなさんは、まず勝手に設定したd1,d2,a の値を変えてやってみてください。結果が変化しないはずですよね。次に異なるn1,n2の組み合わせで屈折の公式と矛盾がないのか？確かめてみてくださ い。

（3）それは酔歩とかランダムウオー ク　(random walk)とか呼ばれています。

酔っぱらいがどちらに足を向けるか判らない状態でいて、歩き回るさまを表していますが、物理現象としては水面に浮かんだ小 さな物体が水分子との衝突によりあっちこっちに動くさまであるブラウン運動とも言えます。　通常は２次元なのですが、そちらへの拡張は後回しにして、１次 元での振る舞いを見てみましょう。つまり酔っぱらいは始め原点(x=0)にいます。次の一歩は右か左か（１次元なので、どちらかです）を乱数を使って決め ましょう。右と左の確率がおなじ場合、乱数は0から1まで同じ確率で現れることをすでに見ていますので、乱数　rが　0.5　以下（0以上）なら左、 0.5以上( 1以下）なら右と決めればいいでしょう。そこで次のようにプログラムしてみます。

do i=1,10
r=rand(0)
if(r>0.5) then
x=x+1
else
x=x-1
endif
write(*,*) i,r,x
enddo

ここでは例えば１０歩歩くことにしたのですが、酔っぱらいの位置座標 x（実は整数にしてあります）を１増やすか（右へ移動）、減らす（左へ移動）ごとに印刷wrireを行っています。今はチェックのためにわざわざr（乱数 の値）も印刷しています。その結果は、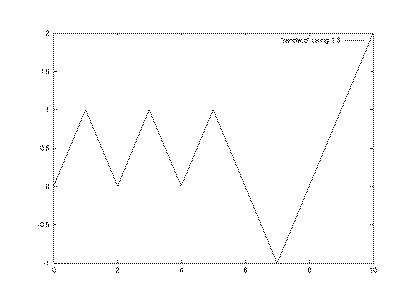ご 覧のようです。

横軸は酔っぱらいの歩数です、縦軸はその位置座標xです。右左右左右 ときて左左、さらに　右右右となって１０歩目では右へ２移動した地点にいます。さてもっと長く歩かせたらどこにいる確率が高いでしょうか？そりゃ右と左と 均等な確率で進むのだから平均としては原点に戻っているだろう！と予想しますよね。これを確かめて見ましょう。ここでは９９歩歩く酔っぱらいを１０００人 持ってきてどこに到達地点（その位置座標）の分布をヒストグラムします。ただし横軸にはｘ座標＋５０でプロットしました。ですから中心値は期待どおりゼロ 付近です。問題はその広がりです。ところでこのヒストグラムは何で１ビンおきになっているのでしょうか？と言う疑問を持ちませんか？実際９９歩歩かせたの ですが、１００歩の時は隣のビンが空になります。（確かめてください）それはそうでしょう！右と左しか行けず奇数歩歩けば必ず奇数地点(x=+-1,+- 3....)しか到達できませんし、反対に偶数歩歩く場合偶数地点(x=0,+-2,+-4....)にしか到達できませんので、こういうヒストグラムに なります。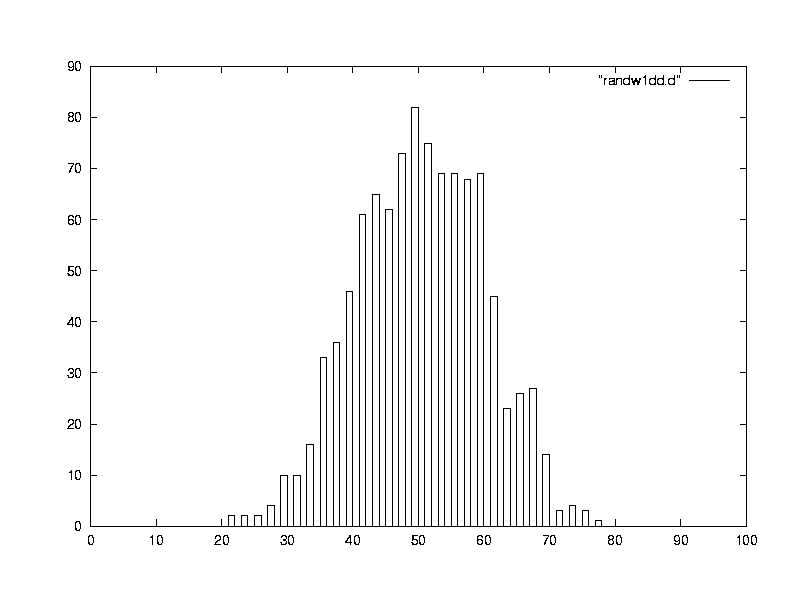ガ ウス分布ににてませんか？平均値はゼロ（上の グラフでは中心を５０ずらしてある）で分散が問題です。分散を計算して酔っぱらいの歩数の関数としてプロットしてみましょう。

さて２次元はどうやりましょうか？　座標はxとyがあります。酔っぱ らいはどちら（どの　ｘ，ｙ）に進むかはさっぱり判りません。ですが、問題を簡単にするためにやはり、１歩xかyの方向へ１歩進むことにしましょう。つま り、　x=x+1,x=x-1,y=y+1,y=y-1 のどれかを必ず行う。そしてその確率はそれぞれ等しいとしてみましょう。プログラムはどうなりますか？その結果を２次元平面に図示すると、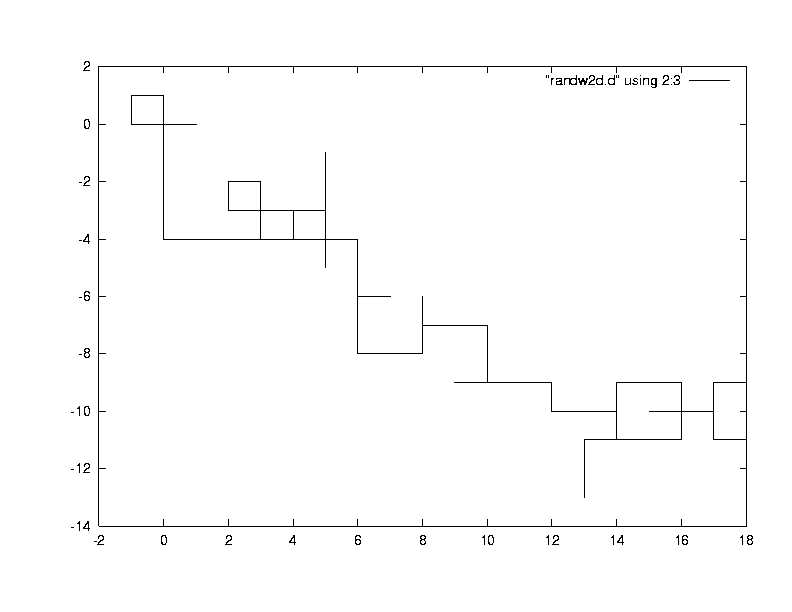

ここでは１００歩歩く酔っぱらいの２次元マップを描いた。所々で線が 止まっているが、これは酔っぱらいが後戻りしたためである。このよっぱらいはなんだかどんどん右下（xが正で大きく、yが負で大きくなる方向）へよって いってますね？？でも一様乱数なので、こんなこともあるが、たくさん酔っぱらいを歩かせると１次元の時と同じように中心値は原点付近でも遠くまで出かける 酔っぱらいが多くなります。これは統計力学では、このようなランダムな動きにもある種の法則性を見つけることができます。すなわち酔っぱらいの歩みは粒子 の拡散現象の１種と考えることもできます。　粒子が全体としてN歩進んだとしましょう。これによって作られるみちすじの持つ性質を考えみましょう、しかし １粒子を追っかけた実験だけでは不十分であることは明らかですね。このような実験を多数回行いその平均（統計力学の用語ではアンサンブル）をとります。そ してN歩目とゼロ歩目（つまり初期位置）との距離R(N)を計算させてみてください。この値のゆらぎは（中心値はゼロのはずですから、ゆらぎは分散です） 　次の量に比例します。

<R(N)*R(N)> - <R(N)><R(N)>

　　これはよく使われる量ですね。分散とも言われます（この量の平方 根は標準偏差です）。ちなみに<x>はｘの平均を表し、

<x>=(x1+x2+x3+.....+xN)/N

xという量の１回目の値がx1,２回目がx2,,,というとき、N回 目まで測定すると、平均値<x>はこの式でかけるというわけです。

ゆらぎは物理の言葉では２次のモーメントです。（ちなみに１次のモー メントは平均のことですね）

統計力学を勉強してもらうと、R(N)はNの0.5乗に比例すること を示すことができます。　これは、酔っぱらいが無限に歩いたなら２次元の全平面をくまなく歩きすべての点に足跡を付けることができることを意味します。こ れを計算物理的には、計算して比べてみましょう。歩く歩数を決めて、何人かの酔っぱらいさんに登場してもらい、到達距離を計算します。そして酔っぱらい人 分の到達距離の平均値を得ることができます。

歩数を変えながら、到達距離の平均値の２乗をプロットしたものが、次 の図です。縦軸を２乗にしたのはR(N)はNの0.5乗という表現よりは、R(N)の２乗はNに比例するというほうが、線形でわかりやすいためです。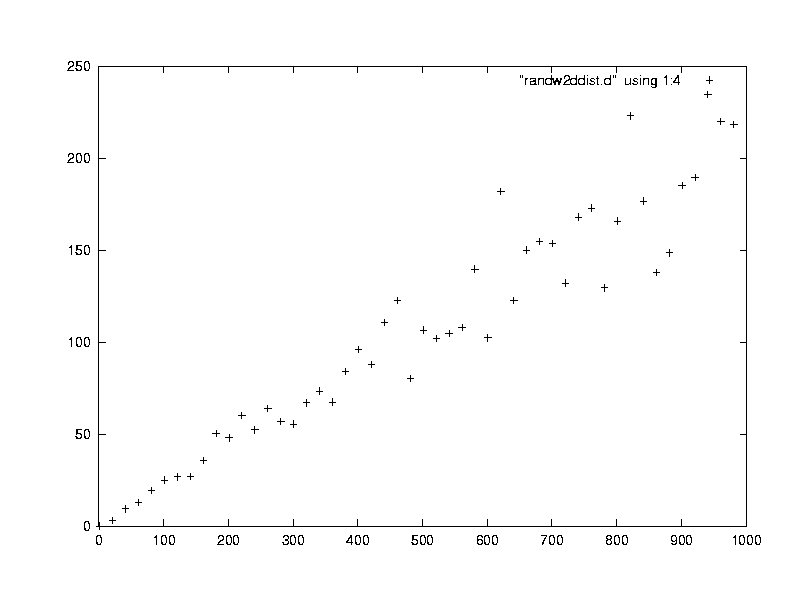

<R^2>-<R>^2はちゃんと酔っぱらいの歩数　Nに比例して大きくな ることが見えます。（^2 は２乗を意味します）

もう一つ酔っぱらいの酔歩とほぼ同じ例で議論します。それはAさんと Bさんが勝負をします。そこでAさんが勝ったら一つ玉をBさんからもらいます。逆も同じ事をします。つまり　Bさんが勝ったら一つ玉をAさんからもらいま す。玉の総数はNとしましょう。またAさんの勝つ確率をpとします。玉がなくなったら負けです。Aさんの勝つ確率を始めにAさんが持っている玉の数kの関 数としてプロットしなさい。という問題を考えてください。

今変数名を定義します：玉の総数=N,最初にAさんが持っている玉の 数=k,ある時点でAさんが持っている玉の数=xa,同様にある時点でBさんが持っている玉の数=xb,Aさんの勝つ確率=p, とします。すると次のプログラムが浮かんできます。xa=0となったらAの負け、反対にxb=0となったら、Aの勝ちです。これで一回終了、これに到達す るまで一回の勝負を続けますが、とりあえず100回までようすを見ます。ヨットすると決着がつかないかもしれませんが、それはそれで引き分けで勝敗に入れ なければ良いです。

k=2　　　　　最初にAが持っている玉の数です。
xa=k　　　　　　Aの始めの位置を決めました。
xb=mab-k　　　Bの始めの位置を決めました。
do i=1,100
r=rand(0)
if(r>p) then
xa=xa+1　　Aが勝てばxaは一つ増える
xb=xb-1 　　同時にBは負けるので一つ減る
else　　　　　　反対に
xa=xa-1　　Aが負ければxaは一つ減る
xb=xb+1 　　同時にBは勝つので一つ増える
endif
write(*,*) i,xa,xb　　　とりあえず結果を印刷してちゃんと動いているいるかどうか確かめる。

ここまではほとんど酔っぱらいの歩みとそっくりです。さてこのあとに xaあるいはxbがゼロとなった　if(xa==0) then の場合どうするのかのか考えて付け加えて、複数回の勝負を行って、確率を計算し上記の問題を解いてください。N=10,p=0.5の場合次の図のようにな ります。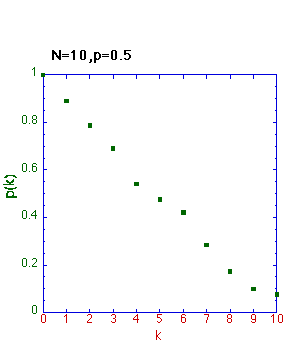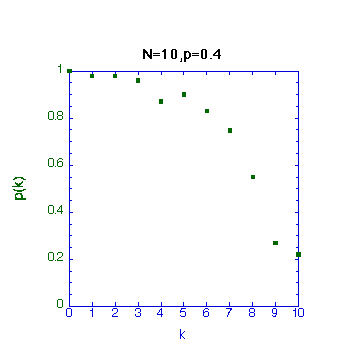またN= 10,p=0.4の場合Aが負けてしまう確率p(k)はkを大きくしてもなかなかゼロに近づかない（本当はk=10 ではp(10)=0.0であるが、１００回の試行では統計的にふらつきゼロになっていない：そもそも他の点に於いても１００回では十分では内、例えば　p =0.5,k=6の点は高い、またp=0.4,k=4の点は低いなど）。一方N=10,p=0.6の場合はどうであろうか？

乱数を使った積分

y=f(x) をx=a からbまで積分する作業は、別の項で、長方形近似、台形近似などなどの方法を紹介しました。ここでは乱数を使った積分を紹介します。

y=f(x) でx=aからbの最大値より大きな値ｃを知っていたとして、一様乱数をx=aからbの間で一つ、y=0からｃの間で一つ発生します。これを(xr,yr) とします。f(x)の積分は面積に相当しますので、長方形ABDCCに対する関数の積分比は、乱数(xr,yr)が長方形内で(xr,f(xr))より小 さい場合の数となります。一方長方形　ＡＢＤＣの面積は(b-a)*cですから、発生した乱数をN個、関数より小さい値（図の斜線部に）入った場合の数を Nrとすると、積分値は（長方形の面積）＊Nr/N　となります。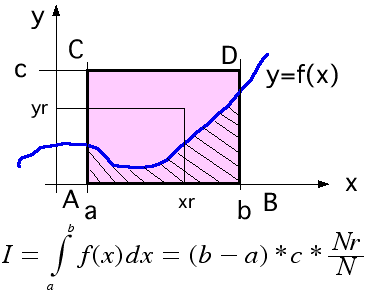 一般の関数について数値積分を実行できます。ただし発散する関数はまともな結果がでませ ん。またc の値が大きすぎると、無駄な乱数ばかり発生して無駄な計算時間を食う、収束が悪いということになります。

乱数を使ったパイの計算

円周率パイが現れる問題を乱数を使って見ましょう。例えば、　(x, y)平面内で0-1の間の一様分布乱数を２個作ります。これをx,yとして、ここでx,yはそれぞれ　1.0　以下で0以上の実数ですから、(x,ｙ）の 組みのつくる平面は、正方形辺の永さ１を作ります。またこの正方形の一辺を半径とする円内の点はx*x+y*y =<1.0　を満たします。　両者の比は面積の比ですから、1:pai/4となります。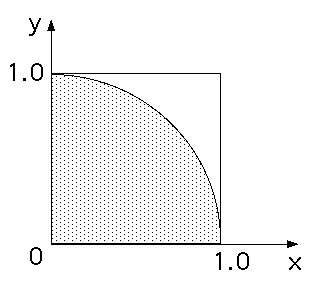つ まり0 から1の間の一様乱数(x,y)の組みをN個作ります。そのうちx*x+y*y =<1.0を満たす組みの数をmとすると、m/Nはpai/4に近づくでしょう。これをNを変えて計算してみました。

　　　Ｎ　　ｍ　　　　パイの値

10 7 2.80000
100 86 3.44000
1000 791 3.16400
10000 7787 3.11480
100000 78704 3.14816
1000000 785286 3.14114

１００万個のNでやっと４桁有効なパイがでます。

もう少し乱数を使った話をしてみましょう。たとえばつぎの問題を考え てください。

いまあなたは銀行の窓口で待つ係りの人になってください。１時間に平 均N人のお客さんが来るとしましょう（来客人数分布はポアソン分布するんですが）。またお客さんとの対応時間はゼロ（つまり書類を受け取るだけ）と仮定し ます。さてあなたの休んでいられる時間（あるお客さんとの対応が終わって次のお客さんが来るまでの時間）分布はどうなるでしょうか？この問題は、バス停で バスを待つ人の待ち時間分布とも一致します。

ゼロから１までの一様乱数をN個生成します。さらにこれを小さい順に 並べ替えます。これを英語ではsort （ソート）といいます。そして、この順番の隣同士の値の差が上の「待ち時間」となります。そして、これをヒストグラム化してやればよろしい。UNIX- likeに３つのプロセスに分けて実行してみました。（１）一様乱数をN個生成、（２）小さい順に並べ替え、（３）ヒストグラム。それぞれの実行ファイル 名を　(1) randgen (2)sort (3) dhistとし、

（１）randgen > rang としてrangなる一様乱数のファイルを作り出します。その結果は次のようになります。ここでは並べ替えによる順番が正しくなったことを示すために１０個 で行います。

0.178395301
0.399677455
0.166598782
0.212121874
0.0619357079
0.0541498438
0.275665492
0.0477572456
0.32103318
0.272733688

（２）sortは(1)の出力ファイル　rangを読み込み、順序を そろえたファイルを作り出します。

do i=1,n
read(*,*) a(i)
enddo
c
do i=1,n
do j=i+1,n
if(a(i)>a(j)) then
w=a(i)
a(i)=a(j)
a(j)=w
endif
enddo
enddo　　　　　　ここで　配列a(i)がまず始めのdo文により読み込まれます。次にif()とdoが２回重なった繰り返しにより順序を入れ替えら れています。

それは次のようにして　実行されます　　　　sort < rang > rano 　　

出力ファイルranoを見てみると、　　more rano

0.0477572456
0.0541498438
0.0619357079
0.166598782
0.178395301
0.212121874
0.272733688
0.275665492
0.32103318
0.399677455
このようにちゃんと小さい順に並んでいます。

（３）これを入力して、隣同士の差のヒストグラムをつくるプログラム を実行して、簡単なヒストグラムをつけて見ました。２０個のビンに分けました。このままでは、２０番目のビンの値は表示されていませんが、0.67ですか ら、１ビンあたり0.07位となります。注目すべきは最初のビンが一番多い？。これは待ち時間分布ですから、最小待ち時間で次のお客があるいはバスが来 る！！！？？ってことを意味します。みなさんの経験と一致しますでしょうか？自然界の全くでたらめな現象の間の時間差ならば、その差が小さい確率がもっと も大きい。と言っています。

0 3
1 2
2 1
3 1
4 0
5 0
6 1
7 1
8 0
9 0
10 0
11 0
12 0
13 0
14 0
15 0
16 0
17 0
18 0
19 0

これで、この結論に到達するには１０個では数が不足していますね。こ ういうとき、統計不足といいます。そこで、１０００個の場合の結果を示します。

0 254
1 221
2 143
3 114
4 74
5 60
6 36
7 37
8 13
9 18
10 10
11 5
12 5
13 4
14 1
15 3
16 0
17 0
18 1
19 1
ただし、軸の倍率は変更しました。なぜなら０−１の間に１０個乱数を落とした、距離分布と、１０００個落とした距離分布は大きく異な るはずだからです。やっぱり最初の最小のビンが最大値を取っています。さてどんな分布をしている、あるいはどんな関数形をしているのでしょうか？これを　 gnuplotで図にしてみましょう。１０００個の場合の出力ファイル名を randwait.d として、

gnuplot "randwait.d" with steps　　　で描いてみましょう。

ふむふむですね。右下がりの関数形ですね。この関数形と特定するため には縦軸をlogスケールにすると物事が見えてきます。そのためには set logscale y とgnuplot内でやってください。再びgnuplot "randwait.d" with steps とすると次の絵が見えます。

やはり予想どおりexponetial（指数関数）ですね。

指数関数はみなさんのもっとも身近な関数ですね。自然界のたとえば物 理学実験でよく用いられるミュー粒子の寿命を測定するときに現れる関数です。そこには、１個１個のミュー粒子ははランダムなタイミングで崩壊します。これ を多数のミュー粒子を測定対象として、測定するとき、短い時間間隔dt内でに崩壊確率は一定値aとしましょう。　[時間tの間生き延び（崩壊することな く）]かつ[t〜t+dtの間に崩壊する確率] dP(t,a)は、二つの確率の積で表されます。すなわち時刻0からt までは崩壊しないので、(1-P(t,a))とt〜t+dtの間に崩壊する確率dt*aであり、

dP(t,a)=(1-P(t,a))*dt*a この微分方程式は変数分離されて、

dP/(1-P)=adt とかけ、これを積分すると、

log(1-P)=-at+c すなわち　　P=1-exp(-at) となります。これが上の図で見えているわけです。