この問題はメールで送る。以下に問題を10問送る、これから(1)~(3) とそれ以外の2問を選んで合計5問の回答を各問いの下に書き足して返信せよ。使ったプログラムはすべて問いに付けよ。
------------------------------ 必答
(1) 0から１までの実数一様乱数を１００個生成し、５０番目に大きな数値を探し出すプログラムを作れ。実際に実行し、その値を srand(1)の場合に記せ。
(2) ガウス型の関数f(x)=exp(-0.278(x-m)**2) の面積を数値積分により計算せよ。mは定数。
(3) フェルマーの定理は、光はある点からある点への伝わる時その時間の最小値となる経路を取るという。均一な媒質中では光は直進するとして、２つの異なる媒質間を光が伝わるとき、最小時間を実現すゆよう、光は折れ曲がる。すなわち屈折の法則が成立する。このことを示せ。ヒントは添付の図でxを乱数を振って探し出せ。
--------------------------
(4)平均値14.3 のポアソン分布で r< 8の確率を小数点下2桁以上の精度で計算せよ、ただしポアソン分布は整数ｒを変数として、 P(r)=[(lamda)**r/r!]*exp(-lamda)
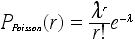で与えられる。λ lamda が平均値である。(5) 万有引力の働く地上から真上にロケットを発射するとき、初速度によりその運動が左右される。地球の引力圏を脱出する速度を地球の質量*万有引力定数の積が１.０の時に、微分方程式を数値的に解くプログラムを用いて探せ。
(6)つぎの関数の最大値と最小値およびこれらを取る点を4桁以上の精度で求めよ。
(-1.5x**4+2.7x**3+2.3)*exp(-0.47x*x-1.24x)/sqrt(2.1x*x+3.0)
(7) xをー0.7から1.2 までの一様乱数として、ｘ＊ｘ の頻度分布の乱数を作り、ヒストグラムとして描け。
(8)２次元で酔歩問題を考える。酔っぱらいは１歩づつ前後左右のどれかの位置へ動くとして、半径１０歩の範囲内のすべての点を１回以上訪れるまでに何歩必要か？
(9)地上で空気抵抗のある投げ上げ問題を考える。空気抵抗が速度の２乗と１乗の両方に比例する項があって、抵抗係数がそれぞれ 0.1と0.4の場合について最高到達点の高さだけを印刷刷る動くプログラムを作れ。物体の質量を1.0とする。
(10) Aさんが12より小さい自然数を思い浮かべ、これをBさんが当てるクイズをプログラムせよ。ただし、AはBの答える値に対し、それより、大きい、当たり、小さいの３種類しか答えないものし、当たるまで繰り返すとする。平均何回の質問で正答に到達できるか？シミュレーションせよ。
計算物理学試験問題 II （31/July/06竹下）
この問題はメールで送る。以下に問題を10問送る、すべての問の回答を各問いの下に書き足してキスト形式（絵やグラフを含んでよい）のレポートをメールで８月４日正午までに返信せよ。問題に、ちゃんと答えよ、何をどうチェックしたか述べよ。プログラムにコメントを
c ここで和=sを計算する
などとやっている事を説明すること。
結果を出して評価せよ。
implicit none を使う事。使ったプログラムはすべて問いに付けよ。
(1) 0から１までの実数一様乱数を１００個生成し、66番目と68番目に大きな数値を探し出すプログラムを作れ。実際に実行し、その値を srand(1)の場合に記せ。
(2) 関数 f(x)=1/sin(1/x) を数値積分により[-1:1]の間で積分せよ。有効数字４桁を保証する手だても述べよ。
(3) フェルマーの定理は、光はある点Aからある点Bへの伝わる時その時間の最小値となる経路を取るという。均一な媒質中では光は直進するとして、２つの異なる媒質間を光が伝わるとき、最小時間を実現するよう、光は折れ曲がる。すなわち屈折の法則が成立する。このことを示せ。ヒントは添付の図でxを乱数を振って探し出せ。媒質の接する線上に光の通る点Cのx座標をとり、x座標を任意（乱数を使って）に設定し、 AC 間を飛ぶ時間とCB間を飛ぶ時間の和をxの関数としてグラフ化して、添付せよ。
(4)平均値11.3 のポアソン分布で r< 8の確率を小数点下３桁以上の精度で計算せよ、ただしポアソン分布は整数ｒを変数として、 P(r)=[(la)**r/r!]*exp(-la) ここで la が平均値である。これとガウス分布の面積がほぼ等しい事を示せ。同じ平均値を使え、またガウス分布の標準偏差はsqrt(la)とせよ。
(5) 万有引力の働く地上から真上にロケットを発射するとき、初速度によりその運動が左右される。地球の引力圏を脱出する速度を地球の質量*万有引力定数の積が１.０の時に、微分方程式を数値的に解くプログラムを用いて探せ。地球の半径を10.0 とせよ。
(6)つぎの関数の最大値と極大値およびこれらを取る点をmの関数として推測して求めよ。
(x**2)*exp(-(x-m)*(x-m))*log(x)
(7) xをー2から2 までの一様乱数として、ｘ＊ｘ＊xー4x＊x の頻度分布の乱数を作り、ヒストグラムとして描け。
(8)２次元で酔歩問題を考える。酔っぱらいは１歩づつ前後左右のどれかの位置へ動くとして、半径12歩の範囲内のすべての点を１回以上訪れるまでに何人の酔っぱらいが必要か？複数の酔っぱらいを動かし試せ。
(9)地上で空気抵抗のある投げ上げ問題を考える。空気抵抗が速度の２乗と１乗の両方に比例する項があって、抵抗係数が高さ(h)の関数でexp(-a*h) の形で依存する場合について最高到達点の高さだけを印刷する動くプログラムを作り動かしその結果を評価せよ。物体の質量を1.0とする。aは抵抗係数の高さ依存係数。
(10) Aさんが25より小さい自然数を思い浮かべ、これをBさんが当てるクイズをプログラムせよ。ただし、AはBの答える値に対し、それより、大きい、当たり、小さいの３種類しか答えないものし、当たるまで繰り返すとする。平均何回の質問で正答に到達できるか？シミュレーションせよ。