竹下徹の応用電磁気学II-2002-2003
0 digital-回路 を マスターする事が目標
そのために、digital回路の例として計算機を作る(黒板や、ノートの上に作る)。
計算機の基本(概念)の把握ー部品と全体像とその統合ー>ソフトウエア(プログラム)
1
(1)計算機はなぜ1と0の2進法でできているのか?
(仮定:正の整数のみの世界で考える)
10進法では、0−9までの10個の数字がある、各数字は1個の素子を
使うとしよう。
任意のn桁の数字を表すには、n・10この素子が必要
同様にr進数では、0−(r-1)までのr個の数字がある、各数字はヘ1個の素子を
使うとしよう。
任意のn桁の数字を表すには、n・rこの素子が必要
N=n・r Nは必要な素子の個数
M=rn (rのn乗) Mは表すことのできる最大値ー1である。
さて問題は、Mが一定(同じMに対して)のとき、何進法をつかえば(rを決める)
Nを最小にできるか? より少ない素子数でまかなえるか?
M=rn これの自然対数をとる。ln(M)=nln(r) --> n=ln(M)/ln(r)
N=nr=rln(M)/ln(r)
Nはrの関数であるとよむ、Nの最小値はdN/dr=0の点で実現
dN/dr=ln(M)/ln(r)+rln(M)(-dln(r)/dr)/(ln(r)2)
= ln(M)/ln(r)-ln(M)/(ln(r)2)
=ln(M)(ln(r)-1)/(ln(r)2)
=0 となるには ln(r)-1=0 -->ln(r)=1 --> r=e=2.718...
つまり2.718進法(?) ーー>3進法がこれに一番近い! 2進法でも悪くない。
電気信号では、2進法が楽! 電圧0(V)と電圧?(V)
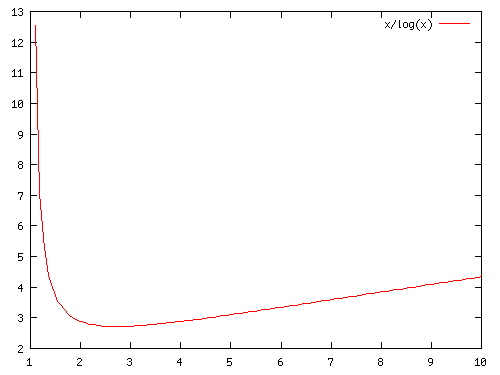
下の図はN(r)(縦軸) vs r (横軸)のグラフ:極小値をr=eで取ることが判る。

2 2進法の論理回路モデル
さて計算機がr進法で作られる経済的に良いという条件で2 か3が良さそうと、電気回路としては2の方が簡単だ、よって計算機はデジタル 0 か 1 でできているのだ。という話しになりました。二つに一つというのは最も簡単な話です。1 か 0 かを、スイッチとランプに対応させて回路を作ります。
1 か 0 か という状態を スイッチの場合、開いている (つまり電流は流れていない)と 閉じている(つまり電流が流れている)に対応させます(世界ではこのようにまるまるである、かそうではないかの 二者択一で動くものが多々あり、数学もできています:後述のBoole代数というものです)。ここでは、スイッチが開いていることを 1 に、スイッチ閉じていることを 0 に対応させましょう。これは単なる定義です。出発するためには何かを定義しないと議論できません。実際この反対を塚事もできますし、結果はおなじです。 スイッチの動作の結果はランプで表されます。 ランプが明るくともっている状態を 1 に、 暗い状態を 0 にしましょう。そうすると、次の回路図が思い浮かびます。(小学生程度)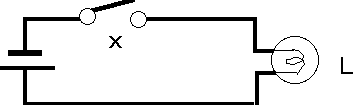 ここではスイッチはx, ランプは Lと表現されています。これをxとLの関係に置き換えることは自然でしょう。 つまりL
は x の関数で、x=0の時(つまり図のようにスイッチが開いているとき)L=0(すなわちランプは暗い:電流が流れていないので)という関係になります、さらに x=1ならば
L=1となります。もうごてごてと説明をかきませんが。このことを表で示すと、
ここではスイッチはx, ランプは Lと表現されています。これをxとLの関係に置き換えることは自然でしょう。 つまりL
は x の関数で、x=0の時(つまり図のようにスイッチが開いているとき)L=0(すなわちランプは暗い:電流が流れていないので)という関係になります、さらに x=1ならば
L=1となります。もうごてごてと説明をかきませんが。このことを表で示すと、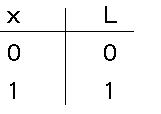 xと L
の間の関係を表す真理表というものになります。左に xの全ての場合を書き(といっても0 か 1 だけですが) 右に対応するLの状態を書きます。これが最も簡単な対応関係です。話しを少々複雑にします。スイッチを二つ持ってきます。つなぎ合わせ方は二つの組み合わせがあります。その一つを示します。
xと L
の間の関係を表す真理表というものになります。左に xの全ての場合を書き(といっても0 か 1 だけですが) 右に対応するLの状態を書きます。これが最も簡単な対応関係です。話しを少々複雑にします。スイッチを二つ持ってきます。つなぎ合わせ方は二つの組み合わせがあります。その一つを示します。![]() ここではスイッチが x1とx2が有り直列につながっています。その真理表はこうなります。
ここではスイッチが x1とx2が有り直列につながっています。その真理表はこうなります。![]() つまり両方のスイッチが 1 の状態(つまり閉じて電流が流れる状態)でない限りランプはつきません。これは真理表の一番下の段に相当します。それ以外はどの組み合わせもランプはつかず 0 です。 この回路はこれから議論してゆくデジタル回路の基本で
AND 回路と呼ばれています。記号(MIL記号) は
つまり両方のスイッチが 1 の状態(つまり閉じて電流が流れる状態)でない限りランプはつきません。これは真理表の一番下の段に相当します。それ以外はどの組み合わせもランプはつかず 0 です。 この回路はこれから議論してゆくデジタル回路の基本で
AND 回路と呼ばれています。記号(MIL記号) は ![]() と書かれます。また論理式では L=x1・x2
と書きます。 同様に二つの入力(x1,x2)に従い出力(L)を取る回路で次のものがあります。
と書かれます。また論理式では L=x1・x2
と書きます。 同様に二つの入力(x1,x2)に従い出力(L)を取る回路で次のものがあります。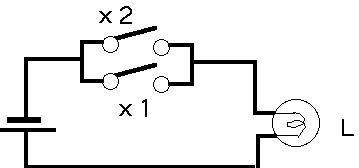 ここではスイッチが x1とx2が有り並列につながっています。その真理表は次のようになります。つまり両方のスイッチが 0 の状態(つまり開いて電流が流れない状態)でない限りランプはつきます L=1
。これは真理表の一番上の段に相当します。それ以外はどの組み合わせもランプはついて 1 です。 この回路はこれから議論してゆくデジタル回路の基本で
OR 回路と呼ばれています。記号(MIL記号) は
ここではスイッチが x1とx2が有り並列につながっています。その真理表は次のようになります。つまり両方のスイッチが 0 の状態(つまり開いて電流が流れない状態)でない限りランプはつきます L=1
。これは真理表の一番上の段に相当します。それ以外はどの組み合わせもランプはついて 1 です。 この回路はこれから議論してゆくデジタル回路の基本で
OR 回路と呼ばれています。記号(MIL記号) は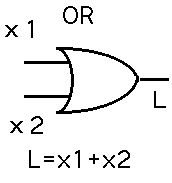
 です。論理式では、 L=x1+x2という式を使います。 さてもう一つスイッチ x が ON
か OFF で電流の流が逆になるスイッチを考えることができます。 つまりx= 0 で電流が流れる(普通のスイッチと反対)そしてか x= 1 で電流がとぎれる(普通のスイッチと反対)。その結果をランプLで表すと、回路は次のようにかける。
です。論理式では、 L=x1+x2という式を使います。 さてもう一つスイッチ x が ON
か OFF で電流の流が逆になるスイッチを考えることができます。 つまりx= 0 で電流が流れる(普通のスイッチと反対)そしてか x= 1 で電流がとぎれる(普通のスイッチと反対)。その結果をランプLで表すと、回路は次のようにかける。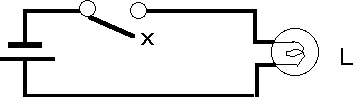 スイッチを上下反対に書いたのは動作が反対であることを明示するためである。これの真理表は
スイッチを上下反対に書いたのは動作が反対であることを明示するためである。これの真理表は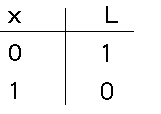 であり、最初の例の反対であり、これをインバーターあるいは NOT 回路と呼ぶ、MIL記号は、
であり、最初の例の反対であり、これをインバーターあるいは NOT 回路と呼ぶ、MIL記号は、![]() であり、式では
であり、式では 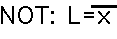 とかかれる。
とかかれる。
さらに組み合わせとして、 こぅいう回路もある。これはMIL記号で
こぅいう回路もある。これはMIL記号で![]() とかかれ、真理表は
とかかれ、真理表は![]() となるので
となるので![]() とかける。
とかける。
また![]() は
は
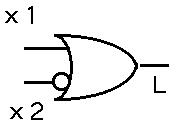
従って ![]() である。
である。