竹下徹の応用電磁気学II-2002 第十回
デジタル通信
コンピュータ間の通信はゼロと1の各ビットのやりとりによるデジタル通信が行われる。ここでは通信が疎外される可能性が有る場合(と言ってもその可能性は低い場合であるが、1ビットたりとも間違ってはいけないので)訂正するための通信技術を取り上げる。コンピュータの内部のような近距離で孤立して制御されている世界では通信の誤りは制御可能で、無いと考える。一方通信距離が大きくなったり、途中に制御不能な存在が予想される場合、通信には間違いが混入する可能性がある。これを議論しよう。また通信距離の増大は同期を取った並列データ転送をほぼ不可能にする。そのためここで考える通信とは物理ケーブル1本によるシリアル(serial)データ転送である。時間方向に瞬間には1ビットのみが送られ、また受信される。
誤りの検出と訂正
情報伝達の途中でどこかのビットひっくり返る可能性の有る(誤りのある)通信を考える。例えば、送りたい情報は"A","B","C"の3つであるとする。これを例えば、3ビットで"A"=001,"B"=011,"C"=111として送る(受け取り方もその内容を知っているとする)。単一誤り(1ビットのみ変化する可能性だけを考えると)受け取る受信符号は次の7つの場合がありうる。"A"=001を送って、最初の1ビットが誤ると、
101として受信される。同様に、011(2ビット目の誤り),000(3ビット目の誤り)そして正しく送られる場合001、合計4つの到着符号がありうる。これを"B",
"C"についても考え合わせると、000が到着すると、"A"=001の1ビット誤りだけが起こりうるので、訂正可能である。しかし、001が到着して場合、"A"=001の正しい通信なのか、"B"=011の2ビット目の誤りなのか2通りの可能性があり、誤りが有ったかどうかすら判らない。そのほか、010と110の受信は訂正可能、101は誤っていることは判るが"A"か"C"かは判断できない。 001と同じく011,
111は誤りがあったのか正しく送られてきたのか判断できない。また100は2重の誤りが重ならない限り起こらないので、ここでは無視できる。
さて付加情報を加えて情報を送り上記のような誤りやその訂正が可能かどうか考える。最も簡単な符号化であるパリティ符号から始めよう。パリティ符号は全データのビットデータの1の数が偶数のとき1をビットとして付け加える(反対に全データのビットデータの1の数が奇数のとき0をビットとして付け加える)偶パリティーがある。{反対のパリティ符号は全データのビットデータの1の数が偶数のとき0をビットとして付け加える(反対に全データのビットデータの1の数が奇数のとき1をビットとして付け加える)奇パリティーがある。}原符号がA1A2A3...Anのときパリティ符号をaとして、(A1A2A3...Ana)として符号化する。 例えば原符号(送信もとのデータ)が3ビットのときは次の表のようになる。
| 原符号 |
偶パリティ |
奇パリティ |
| 000 |
0000 |
0001 |
| 001 |
0011 |
0010 |
| 010 |
0101 |
0100 |
| 100 |
1001 |
1000 |
| 011 |
0110 |
0111 |
| 101 |
1010 |
1011 |
| 110 |
1100 |
1101 |
| 111 |
1111 |
1110 |
符号化効率としては=(原符号ビット数)/(原符号ビット数+付加情報ビット数)=(3)/(3+1)=0.75となる。このパリティ符号は次のようにして作ることができる。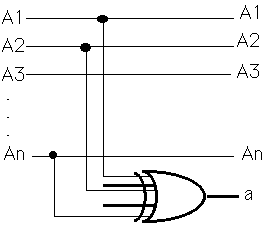 ここでパリティ符号ビットを作るXORは複数入力のXOR
で次の真理表に従うものとする。
ここでパリティ符号ビットを作るXORは複数入力のXOR
で次の真理表に従うものとする。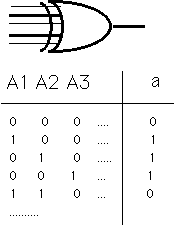 これは最も簡単な 2入力のXORから作られる。例えば3入力のXORは2個の2入力XORの連結で合成可能である。
これは最も簡単な 2入力のXORから作られる。例えば3入力のXORは2個の2入力XORの連結で合成可能である。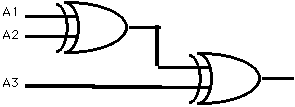 このパリティ符号は単一誤りの検出は可能である、しかし訂正はできない。すなわち例えば 原符号
001に偶パリティを付けて0011 で送信して、誤りが起こったら、1ビット目の誤りでは1011 として受信される。また2ビット目なら0111、3ビット目なら0001、4ビット目なら0010として受信される。1011は正しい到着符号には存在しないので、誤りが起こった事は判る、しかし原符号1010の4ビット目の誤りと区別できない。また0111も正しくないので誤りを認識できるが、0110の4ビット目誤りと区別できない。0001も偶パリティ符号表には存在しないので、誤りが有ることは判るが、元のデータは0011かもしれないので、判らない。同様に1011は1010の4ビット目誤りと区別できないが、偶パリティ符号表には存在しないので、誤りが有ることは判る。つまりパリティー符号では誤りを認識する事ができる。誤りを訂正したい場合、符号系列の空間で十分にデータ同士が放れている必要がある。これは次の図のような概念である。
このパリティ符号は単一誤りの検出は可能である、しかし訂正はできない。すなわち例えば 原符号
001に偶パリティを付けて0011 で送信して、誤りが起こったら、1ビット目の誤りでは1011 として受信される。また2ビット目なら0111、3ビット目なら0001、4ビット目なら0010として受信される。1011は正しい到着符号には存在しないので、誤りが起こった事は判る、しかし原符号1010の4ビット目の誤りと区別できない。また0111も正しくないので誤りを認識できるが、0110の4ビット目誤りと区別できない。0001も偶パリティ符号表には存在しないので、誤りが有ることは判るが、元のデータは0011かもしれないので、判らない。同様に1011は1010の4ビット目誤りと区別できないが、偶パリティ符号表には存在しないので、誤りが有ることは判る。つまりパリティー符号では誤りを認識する事ができる。誤りを訂正したい場合、符号系列の空間で十分にデータ同士が放れている必要がある。これは次の図のような概念である。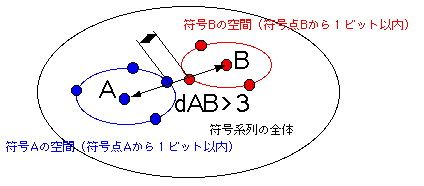 即ちdAB>3ビットならばAの符号の1ビットの誤りとB の1ビットの誤りは空集合で誤りを検出できる。さらにもし符号空間の全ての部分集合が離れているときは(つまり全く集合がくっついていないとき)、単一誤りを全て訂正までできる。
即ちdAB>3ビットならばAの符号の1ビットの誤りとB の1ビットの誤りは空集合で誤りを検出できる。さらにもし符号空間の全ての部分集合が離れているときは(つまり全く集合がくっついていないとき)、単一誤りを全て訂正までできる。
もっと良い(誤り訂正のできる)符号の例としてハミング符号をあげる。パリティーではなんビットデータがあっても1ビットだけ付加情報(検査ビットとよぶ)を加えた。これでは情報を元に戻すことはできないかもしれない。それならばもっと沢山のビットを付加的に付けて冗長性を持たせればノイズ(誤動作によりビットがひっくり返る根元をノイズと言っている)につよいシステムができあがあるかもしれない。いまkビットのデータにrビットの検査ビットを付けるとしよう。しかしいくらでもrを増やせばいいと言うものではない。経済効果つまり符号化効率は最大にしたい。kビットのデータにrビットの検査ビットを付けるときは、符号効率=(k)/(k+r)
で、全ての符号化集合が離れていて単一誤りを全て訂正までできる条件(dAB>3 )は 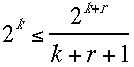 というハミング条件に置き換えることができる。この条件式からk=4のときはr=3で等号が成立する。同様にk=11
then r=4, k=26 then r=5, k=57 then r=6 であり、 例えば32ビットデータ(k=32)の時はr=6で有れば不等号が成立する事が判る。ではいったいどうやって符号を付けるかみてみよう。具体例としてk=4,r=3の場合を考える。データはabcdの4ビットで、誤り訂正用の符号(これをハミング符号という)がp0,p1,p2の3ビットである。ちなみに符号効率=(4)/(4+3)=4/7=0.57である。試しにp0=a+b+c,p1=b+c+d,p2=a+b+dで付けてみよう。ここでa,b,c,dはそれぞれのビットでゼロか1である。和は2進法で取る。つまりパリティの時と同じようにXORである。異なるのは複数の符号かビットを持つ点である。これを表にすると次のようになる。
というハミング条件に置き換えることができる。この条件式からk=4のときはr=3で等号が成立する。同様にk=11
then r=4, k=26 then r=5, k=57 then r=6 であり、 例えば32ビットデータ(k=32)の時はr=6で有れば不等号が成立する事が判る。ではいったいどうやって符号を付けるかみてみよう。具体例としてk=4,r=3の場合を考える。データはabcdの4ビットで、誤り訂正用の符号(これをハミング符号という)がp0,p1,p2の3ビットである。ちなみに符号効率=(4)/(4+3)=4/7=0.57である。試しにp0=a+b+c,p1=b+c+d,p2=a+b+dで付けてみよう。ここでa,b,c,dはそれぞれのビットでゼロか1である。和は2進法で取る。つまりパリティの時と同じようにXORである。異なるのは複数の符号かビットを持つ点である。これを表にすると次のようになる。
| a |
b |
c |
d |
p0 |
p1 |
p2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
1 |
1 |
| 0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
0 |
1 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
1 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
さてこの場合0000がデータで送られる場合、符号化ビット000がついて 0000000が送られる。これに単一誤りが生じて1ビット狂う場合、1000000,0100000,0010000,0001000,0000100,0000010,0000001の7通りの間違え方がある。全ての誤ったデータは上のデータ表になく「誤り」があったことが判る。さて訂正は出きるか?ここで誤り訂正用の3つのビット(シンドロームビットという)を導入する。シンドロームビットS0,S1,S2はそれぞれS0=a+b+c+p0,S1=b+c+d+p1,S2=a+b+d+P2で作る。ビット誤りが無ければもともとa+b+c=p0なのでS0=p0+p0=ゼロ のはずである。他のS1,S2も同様。つまり誤りが無ければ全てのS0,S1,S2は全部ゼロである。もしゼロ出ないなら誤りが有ったことを示す。単一誤りを仮定して次の表を作る。つまりどれかのビットに誤りが生じた場合(複数のビットの誤りは単一誤りではあり得ない)シンドロームビットS0,S1,S2はどうなるかを示す表である。
| a |
b |
c |
d |
p0 |
p1 |
p2 |
S0 |
S1 |
S2 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
| 0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
よってこのシンドロームビットの組み合わせ(S0,S1,S2) を見るとどのビットに誤りがあるか解る。たとえば先ほどの例で0000000を送って単一誤りで1000000が来た(受け取られた)場合、S0=1,S1=0,S2=1
であるからこの表の最上段のaの誤りであることが判明する。さて更にパリティビットを回路で作ったようにここでもシンドロームビットS0,S1,S2
を作ってみよう。これをハミング符号エンコーダー(ハミング符号化回路)とよぶ。図の箱 (R0,R1,R2)は1ビットのレジスターで入ったデータ(1ビット)は次のタイミングで出力される1ビットシフトレジスターでもある。これらのレジスターはD-FF で有り、あらかじめゼロにセットしてあるとしよう。さらにすべてのレジスターは同一クロックで同期して動作する。そのたのXORなどでは信号の遅延はないとする。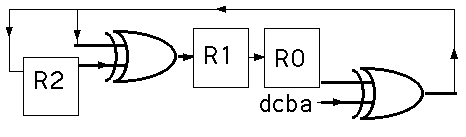
| clock |
R2 |
R1 |
R0 |
| 1 |
a+0 |
a+0 |
0 |
| 2 |
b+0 |
a+b |
a+0 |
| 3 |
a+c |
a+b+c |
a+b |
| 4 |
a+b+d |
b+c+d |
a+b+c |
|
=p2 |
=p1 |
=p0 |
この表からわかるようにRi はpiに等しくハミング符号検査ビットである、よってこのRiがハミングエンコーダーとなる。さてシンドロームビット S0,S1,S2は次の回路で検出できる。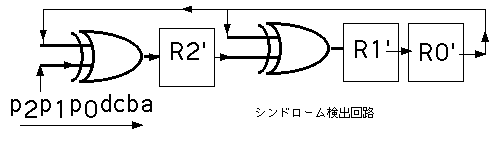
| clock |
R2' |
R1' |
R0' |
| 1 |
a |
0 |
0 |
| 2 |
0+b |
a+0 |
0 |
| 3 |
c |
b |
a |
| 4 |
d+a |
c+a |
b |
| 5 |
p0+b |
d+a+b |
c+a |
| 6 |
p1+c+a |
p0+b+c+a |
d+a+b |
| 7 |
p2+d+a+b |
p1+c+a+d+a+b |
p0+b+c+a |
|
=S2 |
=S1 |
=S0 |
シンドローム符号 S0,S1,S2を計算できることがわかる。シンドローム符号がわかればデータの誤りを訂正出きることが判っているので通信の信頼性を保つことができる。
1ビットの誤りを自動的に訂正する回路は次のようなる。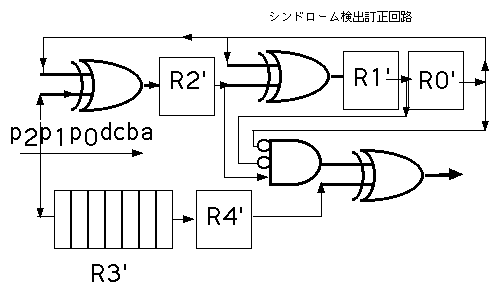 最終出力が訂正された符号である。
最終出力が訂正された符号である。
実はこれらの図がk=4でr=3の時ばかりでなく拡張は容易で、k=26,r=5の時のハミング符号エンコーダー(符号化回路)は次の図で十分である。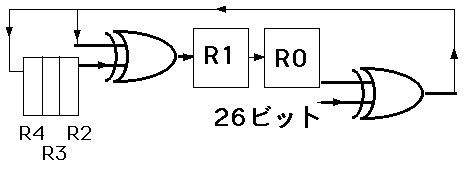 同様にデコーダー(複合化回路:つまり誤り訂正回路)の26ビットデータ+ハミング符号5ビット=31ビットでは、上記のR3'を31段シフトレジスターにし、R2'を3段にすればよい。もちろん左からの入力は31ビットである。
同様にデコーダー(複合化回路:つまり誤り訂正回路)の26ビットデータ+ハミング符号5ビット=31ビットでは、上記のR3'を31段シフトレジスターにし、R2'を3段にすればよい。もちろん左からの入力は31ビットである。
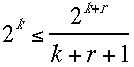 というハミング条件に置き換えることができる。この条件式からk=4のときはr=3で等号が成立する。同様にk=11
then r=4, k=26 then r=5, k=57 then r=6 であり、 例えば32ビットデータ(k=32)の時はr=6で有れば不等号が成立する事が判る。ではいったいどうやって符号を付けるかみてみよう。具体例としてk=4,r=3の場合を考える。データはabcdの4ビットで、誤り訂正用の符号(これをハミング符号という)がp0,p1,p2の3ビットである。ちなみに符号効率=(4)/(4+3)=4/7=0.57である。試しにp0=a+b+c,p1=b+c+d,p2=a+b+dで付けてみよう。ここでa,b,c,dはそれぞれのビットでゼロか1である。和は2進法で取る。つまりパリティの時と同じようにXORである。異なるのは複数の符号かビットを持つ点である。これを表にすると次のようになる。
というハミング条件に置き換えることができる。この条件式からk=4のときはr=3で等号が成立する。同様にk=11
then r=4, k=26 then r=5, k=57 then r=6 であり、 例えば32ビットデータ(k=32)の時はr=6で有れば不等号が成立する事が判る。ではいったいどうやって符号を付けるかみてみよう。具体例としてk=4,r=3の場合を考える。データはabcdの4ビットで、誤り訂正用の符号(これをハミング符号という)がp0,p1,p2の3ビットである。ちなみに符号効率=(4)/(4+3)=4/7=0.57である。試しにp0=a+b+c,p1=b+c+d,p2=a+b+dで付けてみよう。ここでa,b,c,dはそれぞれのビットでゼロか1である。和は2進法で取る。つまりパリティの時と同じようにXORである。異なるのは複数の符号かビットを持つ点である。これを表にすると次のようになる。 ここでパリティ符号ビットを作るXORは複数入力のXOR
で次の真理表に従うものとする。
ここでパリティ符号ビットを作るXORは複数入力のXOR
で次の真理表に従うものとする。 これは最も簡単な 2入力のXORから作られる。例えば3入力のXORは2個の2入力XORの連結で合成可能である。
これは最も簡単な 2入力のXORから作られる。例えば3入力のXORは2個の2入力XORの連結で合成可能である。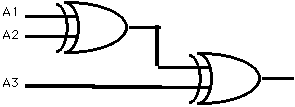 このパリティ符号は単一誤りの検出は可能である、しかし訂正はできない。すなわち例えば 原符号
001に偶パリティを付けて0011 で送信して、誤りが起こったら、1ビット目の誤りでは1011 として受信される。また2ビット目なら0111、3ビット目なら0001、4ビット目なら0010として受信される。1011は正しい到着符号には存在しないので、誤りが起こった事は判る、しかし原符号1010の4ビット目の誤りと区別できない。また0111も正しくないので誤りを認識できるが、0110の4ビット目誤りと区別できない。0001も偶パリティ符号表には存在しないので、誤りが有ることは判るが、元のデータは0011かもしれないので、判らない。同様に1011は1010の4ビット目誤りと区別できないが、偶パリティ符号表には存在しないので、誤りが有ることは判る。つまりパリティー符号では誤りを認識する事ができる。誤りを訂正したい場合、符号系列の空間で十分にデータ同士が放れている必要がある。これは次の図のような概念である。
このパリティ符号は単一誤りの検出は可能である、しかし訂正はできない。すなわち例えば 原符号
001に偶パリティを付けて0011 で送信して、誤りが起こったら、1ビット目の誤りでは1011 として受信される。また2ビット目なら0111、3ビット目なら0001、4ビット目なら0010として受信される。1011は正しい到着符号には存在しないので、誤りが起こった事は判る、しかし原符号1010の4ビット目の誤りと区別できない。また0111も正しくないので誤りを認識できるが、0110の4ビット目誤りと区別できない。0001も偶パリティ符号表には存在しないので、誤りが有ることは判るが、元のデータは0011かもしれないので、判らない。同様に1011は1010の4ビット目誤りと区別できないが、偶パリティ符号表には存在しないので、誤りが有ることは判る。つまりパリティー符号では誤りを認識する事ができる。誤りを訂正したい場合、符号系列の空間で十分にデータ同士が放れている必要がある。これは次の図のような概念である。 即ちdAB>3ビットならばAの符号の1ビットの誤りとB の1ビットの誤りは空集合で誤りを検出できる。さらにもし符号空間の全ての部分集合が離れているときは(つまり全く集合がくっついていないとき)、単一誤りを全て訂正までできる。
即ちdAB>3ビットならばAの符号の1ビットの誤りとB の1ビットの誤りは空集合で誤りを検出できる。さらにもし符号空間の全ての部分集合が離れているときは(つまり全く集合がくっついていないとき)、単一誤りを全て訂正までできる。


 最終出力が訂正された符号である。
最終出力が訂正された符号である。 同様にデコーダー(複合化回路:つまり誤り訂正回路)の26ビットデータ+ハミング符号5ビット=31ビットでは、上記のR3'を31段シフトレジスターにし、R2'を3段にすればよい。もちろん左からの入力は31ビットである。
同様にデコーダー(複合化回路:つまり誤り訂正回路)の26ビットデータ+ハミング符号5ビット=31ビットでは、上記のR3'を31段シフトレジスターにし、R2'を3段にすればよい。もちろん左からの入力は31ビットである。