竹下徹の応用電磁気学II-2002　第三回

3ブール代数continued　

ブール代数の計算ではであるような証明がある。

またであることを示す事が出きる。
つまり左辺第三項は無くてもよいので不要項と呼ばれる、ブール代数の計算をして持って行く事も出きる。

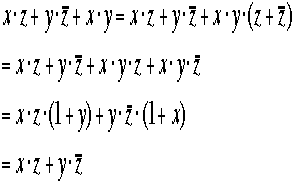
この式はf(a,b,c,....)=a・f(1,b,c,...)+a・f(0,b,c,...)というシャノンの定理を使うと楽になる、ただし、a=zと思う。ブール代数の集大成的なシャノンの仕事にちなんでのことであろう。

として
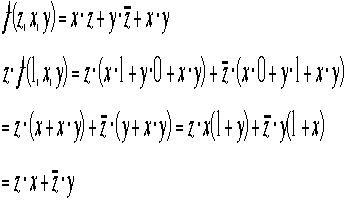と示される。

不要項の存在を使う　も簡単に示される。このような式は全て真理表でも示されることは言うまでもない。

ブール代数では双対性がある：式内のすべての　+ -> ・、・=>+, 1=>0,0=>1 置き換えを行った式は、また正しい。というもので、が成立することが判っているので、 ==>双対性を使って置き換えて
も成立することが双対性です。
あるいは一番上の式から
なので、これを双対性で置き換えた

も示される。

また拡張ドモルガン則：　　式内のすべての　+ -> ・、・=>+, 1=>0,0=>1 ,各変数の否定を取って
置き換えを行った式は、基の式全体の否定である。というもので、 ===>置き換え

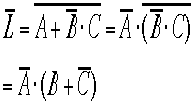
これはL'に等しい：。この応用として次の３つの式を示すことができる。

を示せ
を示せ
を示せ

すべての回路はNAND あるいは NORのみで表現できる！
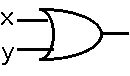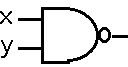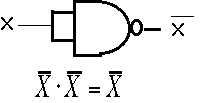例えば、OR回路をNANDで表せという問題は、NAND回路がであることを思い出すと、OR回路を使い、またであることをつかいので、OR回路を作ることが出きる。これを回路図で示すと、入力Ｘ，Ｙ　　に関して X+Y をNAND　回路のみで描く。 X+Yは OR 回路です。ですね。　NANDはです、X=Yのとき NAND　　の出力はよりNOT回路を作ることができます。さて次はドモルガンの法則により、　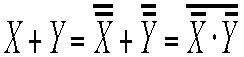という式の回路図は、次のようになります。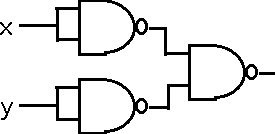同様に入力Ｘ，Ｙ　　に関して X・Y をNAND　回路のみで書け。あるいは入力Ｘ，Ｙ　　に関して X+Y をNOR　回路のみで書け。入力Ｘ，Ｙ　　に関して X・Y をNOR　回路のみで書け。という問題がありえます。自分で解いてください。

さていままで入力はせいぜい２つを扱って来ましたが、３つ以上になることも考えておきましょう。そんなとき役に立つ方法にカルノー図あるいはベイチ図による簡単法があります。それを紹介します。まずはよく判っている２入力回路です。２入力では組合せは２の２乗つまり４通りあります。真理表を書くとき縦に４個並びますね。これを２次元平面内に描いてしまいます。つまりこういう図です。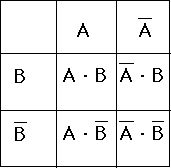横方向に２つどうように　縦方向にの場合をとります。従ってA・Bの箱は　A=1 and B=1のときに該当します。これをの場合に描いてみます。この式はであり、Aです、これを カルノー図に書き入れると次のようになります。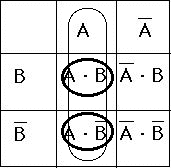縦に長いつらながりの丸を描くことができます。これをAと読みます。こうやって視覚的に直感的にブール代数の計算をやってのける術があります。さてこれを３変数まで拡張するととても便利です。しかし３次元的に図を描いては訳が分かりませんので、平面内に描いてしまします。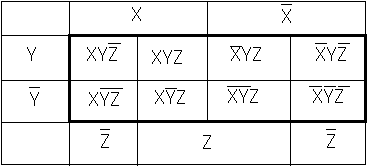中央の太線内８つのカラムが２の３乗＝８個の分類です。この８つがそれぞれX,Y,Z の組み合わせで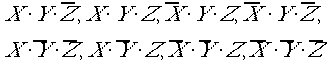とあらわされます。たとえばを表す位置は、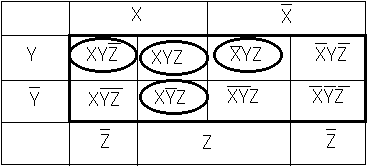となります。これを解釈します。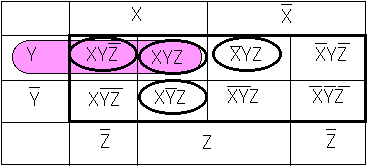Yを含む横長の丸は二つの小丸を含みとの両方を含むためこの組みでXYという項を表します。以下同様に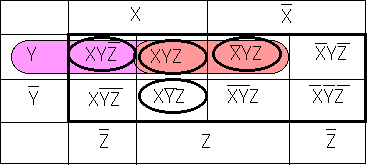の示す領域はとの両方を含みますので、ＹＺです。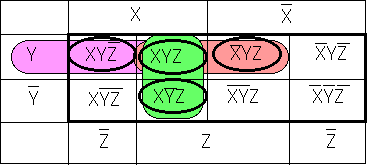最期に緑の領域はとを含みますので、ＸＺとなりまう。従って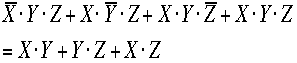となることが判ります。これがカルノー図あるいはベイチ図のつかいかたデス。