抾壓揙偺墳梡揹帴婥妛II-2002丂戞屲夞
5僟僀僆乕僪偲僩儔儞僕僗僞乕梡偄偨AND,
OR, NOR, NAND and XOR夞楬
n宆敿摫懱偲p宆敿摫懱傪愙崌偟偰僟僀僆乕僪傪嶌偭偨丅偦偺摿挜偼丄弴僶僀傾僗偱偼丄掞峈偑彫偝偔丄媡僶僀傾僗偱偼掞峈偑嬌抂偵戝偒偄帠偱偁偭偨丅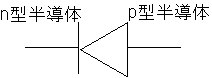
偙傟傪嬌抂偵偟偰偟傑偆丟僨僕僞儖壔偡傞
偮傑傝弴僶僀傾僗揹埵偱偼丄掞峈僛儘丄
媡僶僀傾僗揹埵偱偼丄掞峈柍尷戝
偲峫偊傞丅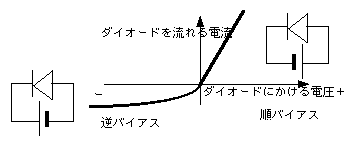
傑軅綋d埵偼俀偮偁偭偰丄榑棟偺
乭侾乭偲乭侽乭偵憡摉偡傞偑丄
捠忢丄乭侽乭偼僛儘揹埵偮傑傝丄愙抧偵偲傞傋偒偱偁傠偆丅傑偨偙偺庼嬈偱偼惓偺揹埵=Vcc傪乭侾乭偵偲傞榑棟傪梡偄傞丅+5V傪偦偺揹埵偲偡傞TTL(Transister
Transister Logic)偑桳柤偱偁傞丅乮嬤擭偼憗偄丄彫揹椡夞楬偺偨傔偵揹埵偼偳傫偳傫掅偔側偭偰偄傞丅偙偆偡傞偲僲僀僘偲偺愴偄偲側傞乯
偝偰嵍偺夞楬傪峫偊傛偆丄擖椡揹埵偑僛儘偮傑傝丄榑棟偱侽偺偲偒丄揹棳偼Vcc偐傜掞峈傪捠偟丄僟僀僆乕僪傪偲偍偭偰擖椡傊棳傟傞丅偙偺偲偒偺弌椡偺揹埵偼擖椡偲摨偠偔僛儘偱偁傞丅傑偨擖椡揹埵偑崅偄=Vcc偮傑傝丄榑棟偱1偺偲偒丄揹棳偼僟僀僆乕僪偺偨傔偵棳傟側偄丅傛偭偰偙偺偲偒偺弌椡偺揹埵偼Vcc偑揱傢傞偺偱崅偄偮傑傝1偱偁傞丅
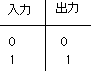
偙傟偼榑棟夞楬偲偟偰偼丄弌椡z=擖椡x偱偁傞丅
偱偼栤戣丗塃恾偼偳偆偩傠偆丅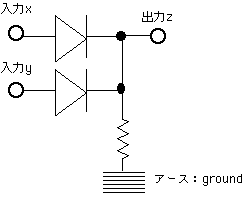 偙偙偱丄愙抧晹偺夞楬偼徣偄偨丅師恾偼
偙偙偱丄愙抧晹偺夞楬偼徣偄偨丅師恾偼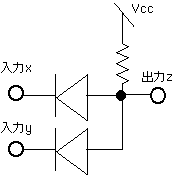 丠丠丠
丠丠丠
僩儔儞僕僗僞
僟僀僆乕僪偼n宆敿摫懱偲p宆敿摫懱傪愙崌偟偰嶌偭偨丅偮傑傝俀屄偱嶌偭偨偺偱丄俀抂巕偁偭偰僟僀亖俀偩偭偨丅
偙傟偵懳偟偰俁屄偱嶌傞偲僩儔亖俁僕僗僞乕偲側傞丅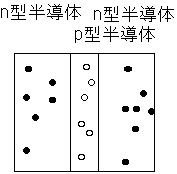
慻傒崌傢偣偼俀庬椶丄npn偐丂pnp偐丅恀傫拞偼敄憌偲偡傞丅
傑偨偙傟偵揹埑傪偐偗傞偑丄偐偗曽偼丄俁偮偺抂巕偑偁爞閭虃艁A揹抮偑俀偮昁梫偲側傞丅傑偢堦偮傔偺揹抮傪偍偔丅偙傟偼僟僀僆乕僪側偺偱丄p懁偵僾儔僗偑偁傟偽偙偺僟僀僆乕僪偵偼揹棳偑棳傟傞丅偙傟傪巭傔傞偨傔偵僗僀僢僠傪偮偗丄偝傜偵斀懳偺n懁偵偵偼傛傝戝偒側揹埑傪偐偗傞丅偙傟傪僄儈僢僞愙抧偲屇傇丅
僗僀僢僠傪暵偠傞偲揹棳偑棳傟傞偙偲偼忋偱弎傋偨丅僗僀僢僠傪奐偔偲丄僾儔僗偺儂乕儖偲塃偺揹巕偼偔偭偮偄偰柍偔側偭偰丄慡晹柍偔側傞偲丄揹棳偼棳傟側偔側傞丅偙偙偱巭傑傞丅偨偲偊丄嵍偺n偺崅偄揹埑偑偁偭偨偲偟偰傕丅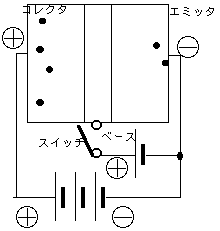 偙偺忬懺偱丄僗僀僢僠傪暵偠傞丅偡傞偲恀傫拞偺p敿摫懱晹偵儂乕儖偑嫙媼偝傟傞丅僀儊乕僕偲偟偰偼壓偺抂巕晅嬤偵儂乕儖偑弌偰偔傞丅僄儈僢僞傪偱偨揹巕偺堦晹偼偙偺嫙媼偝傟偨儂乕儖偲寢崌偟偰柍偔側傞偑丄戝晹暘偼嵍傊棳傟傞丅偙偆偟偰丄儀乕僗偵揹埑偑偐偐傞乮僾儔僗乯偲僐儗僋僞偐傜僄儈僢僞偵揹棳偑側偑傟傞偲偄偆丄夞楬偑偱偒偁偑傞丅偙傟傪壓偺恾}偺傛偆偵夞楬恾偲偡傞丅揹棳偺曽岦偲揹巕偺堏摦曽岦偼媡丅
偙偺忬懺偱丄僗僀僢僠傪暵偠傞丅偡傞偲恀傫拞偺p敿摫懱晹偵儂乕儖偑嫙媼偝傟傞丅僀儊乕僕偲偟偰偼壓偺抂巕晅嬤偵儂乕儖偑弌偰偔傞丅僄儈僢僞傪偱偨揹巕偺堦晹偼偙偺嫙媼偝傟偨儂乕儖偲寢崌偟偰柍偔側傞偑丄戝晹暘偼嵍傊棳傟傞丅偙偆偟偰丄儀乕僗偵揹埑偑偐偐傞乮僾儔僗乯偲僐儗僋僞偐傜僄儈僢僞偵揹棳偑側偑傟傞偲偄偆丄夞楬偑偱偒偁偑傞丅偙傟傪壓偺恾}偺傛偆偵夞楬恾偲偡傞丅揹棳偺曽岦偲揹巕偺堏摦曽岦偼媡丅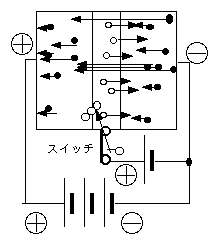
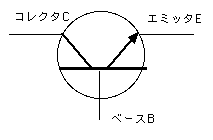
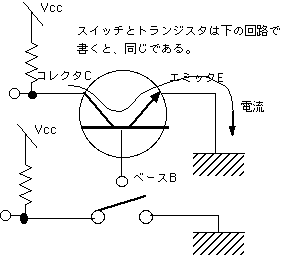 偩傟偑B傪墴偡偐傪僩儔儞僕僗僞偵抲偒姺偊偨丄弌椡偼C偱偁傞丅
偩傟偑B傪墴偡偐傪僩儔儞僕僗僞偵抲偒姺偊偨丄弌椡偼C偱偁傞丅
僩儔儞僕僗僞偵傛傞NOT夞楬npn愙崌偺傛傞僩儔儞僕僗僞傪塃偺傛偆偵昞偡偲偒丄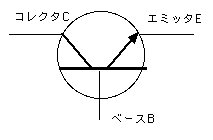
pnp愙崌偺僩儔儞僕僗僞偼丄偙偆側傞偙偲傪帵偣丅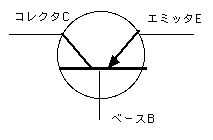 傑偢僩儔儞僕僗僞傪巊偭偰NOT夞楬傪嶌傞丅
傑偢僩儔儞僕僗僞傪巊偭偰NOT夞楬傪嶌傞丅
擖椡丄弌椡偼丂惓偺揹埑偑崅偄Vcc偺帪傪1偲偟丄
揹埑偑僛儘偮傑傝愙抧揹埑偺偲偒傪0偲偡傞丅
偙偺夞楬傪挷傋傛丅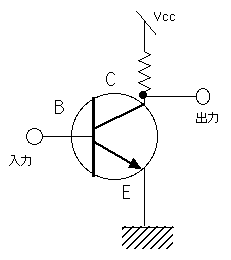
僽乕儖戙悢偺抣偺嵞掕媊
x=1: 揹埑丂崅偄乮揹棳傪棳偡偙偲偑偱偒傞乯
x=0: 揹埑丂掅偄乮揹棳傪棳偡偙偲偑偱偒側偄乯僩儔儞僕僗僞偼丄榑棟夞楬偺僗僀僢僠偲偟偰偽偐傝偱側偔丄傾儞僾乮揹棳憹暆夞楬乯偲偟偰傕梡偄傜傟傞丅偙傟傪愢柧偡傞丅乮墳梡揹帴婥I偺榖偟乯僩儔儞僕僗僞偱僄儈僢僞愙抧偺偲偒偺揹棳偺棳傟偼丄戝敿偼僐儗僋僞偐傜僄儈僢僞傊棳傟傞丄偟偐偟僐儗僋僞偐傜儀乕僗傊偺揹棳傕懚嵼偡穫閬B偙傟傜傪丄ICE,ICB偲偡傞偲丄
ICE>>ICB 偲偡傞帠偑偱偒傞丅擖椡揹棳傪ICB,弌椡揹棳
傪ICE擖側偺偱丄彫揹椡偺擖椡偐傜戝揹椡乮掞峈傪擖弌椡
偵偮偗傟偽揹椡偲側傞乯偵曄姺偡傞丄傾儞僾偑偱偒偁偑傞丅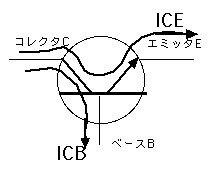 http://lib1.nippon-foundation.or.jp/1998/0149/mokuji.htm
http://lib1.nippon-foundation.or.jp/1998/0149/mokuji.htm
偙偙偵堈偟偄愢柧偑偁傞丅
僟僀僆乕僪偲僩儔儞僕僗僞偵傛傞NAND/NOR夞楬
僩儔儞僕僗僞傪巊偭偰NOT夞楬傪嶌偭偨丅僟僀僆乕僪傪巊偭偨AND偲慻傒崌傢偣傞丄偮傑傝AND夞楬偺弌椡傪NOT夞楬偺擖椡偵偄傟偰傗傞偲丄NAND夞楬偑偱偒偁偑傞丅摨條偵偟偰僟僀僆乕僪傪巊偭偨OR偲
NOT夞楬傪慻傒崌傢偣傞丄偮傑傝OR夞楬偺弌椡傪NOT夞楬偺擖椡偵偄傟偰傗傞偲丄NOR夞楬偑偱偒偁偑傞丅
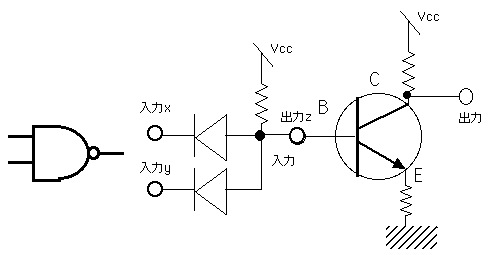
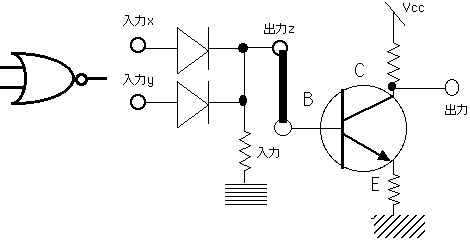
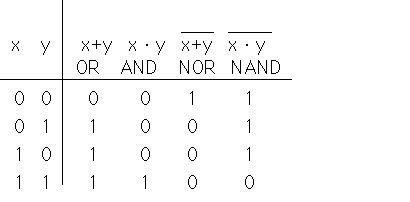
XOR夞楬
XOR=eXclusive乮攔懠揑乯 OR 夞楬偼忋婰恀棟昞偺斀墳傪偡傞夞楬偱偁傞丅
攔懠揑偲偼丄x偲y偵偮偄偰偍屳偄偼堎側傞乮攔懠乯偲偒偼丄弌椡偑侾偲側傞丅
偙傟傪AND,OR,NOT偱嶌傞偲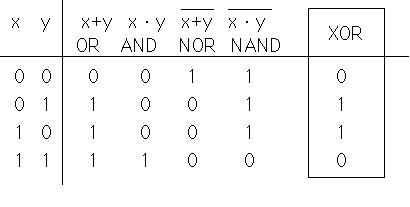
XOR=eXclusive乮攔懠揑乯 OR 夞楬偼忋婰恀棟昞偺斀墳傪偡傞夞楬偱偁傞丅
攔懠揑偲偼丄x偲y偵偮偄偰偍屳偄偼堎側傞乮攔懠乯偲偒偼丄弌椡偑侾偲側傞丅
偙傟傪AND,OR,NOT偱嶌傞偲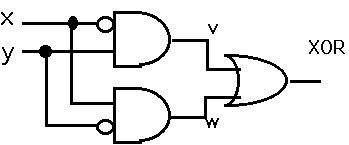
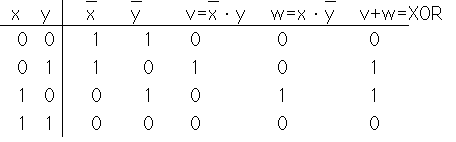
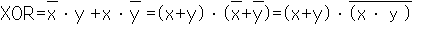
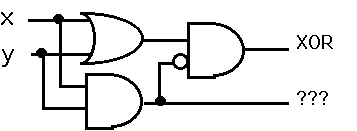
楙廗栤戣
(1) 俀擖椡偺椉曽偺抣偑堦抳偟偨偲偒偺傒弌椡侾傪弌偡夞楬傪暋悢嶌傟丅乮恀棟昞丄夞楬恾丄Bool戙悢偺寁嶼傪嵟掅尷娷傓偙偲乯
夝摎丗擖椡傪x,y丄弌椡傪Z偲偡傞偲丄恀棟昞偼師偺傛偆偵側傞丅偙傟傪枮偨偡夞楬偼丄傑偢偙傟偑XOR偺NOT偱偁傞偙偲偐傜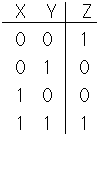
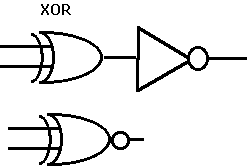 偱偁傞丅傑偨偙偺恀棟昞傪昞偡BOOL戙悢幃偼Z=X丒Y+X丒Y偱偁傞偙偲傛傝丄師偺夞楬傕夝偱偁傞偙偲偑敾傞丅
偱偁傞丅傑偨偙偺恀棟昞傪昞偡BOOL戙悢幃偼Z=X丒Y+X丒Y偱偁傞偙偲傛傝丄師偺夞楬傕夝偱偁傞偙偲偑敾傞丅 偝傜偵
偝傜偵 傛傝丄師偺夞楬傕夝偱偁傞丅
傛傝丄師偺夞楬傕夝偱偁傞丅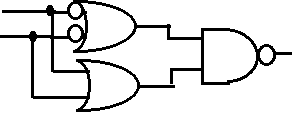
乮俀乯俁偮偺擖椡傪帩偮夞楬偱俀屄埲忋偺擖椡偑侾偺偲偒弌椡侾傪弌偡夞楬傪暋悢偮偔傟丅偙傟傕夞楬偵偛偲偵丂恀棟昞丄夞楬恾丄Bool戙悢偺寁嶼傪嵟掅尷娷傓偙偲丅
3擖椡傪x,y,z丄弌椡傪F偲偡傞偲丄恀棟昞偼師偺傛偆偵側傞丅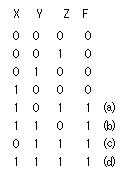 偒傟偄偱偼柍偄夞楬偱傑偢嶌傞丅呟呠呡呣偺偦傟偧傟偺応崌偺夞楬傪嶌傝OR傪庢傟偽傛偄偺偱丄
偒傟偄偱偼柍偄夞楬偱傑偢嶌傞丅呟呠呡呣偺偦傟偧傟偺応崌偺夞楬傪嶌傝OR傪庢傟偽傛偄偺偱丄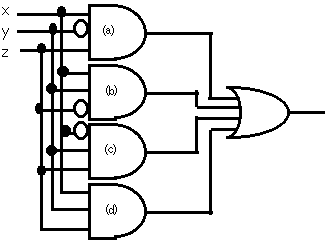 Bool戙悢偱偼丄F=X丒Y丒Z+X丒Y丒Z+X丒Y丒Z+X丒Y丒Z
Bool戙悢偱偼丄F=X丒Y丒Z+X丒Y丒Z+X丒Y丒Z+X丒Y丒Z
=X丒Y丒Z+X丒Y丒Z+(X+X)丒Y丒Z=X丒Y丒Z+X丒Y丒Z+Y丒Z
=X丒(Y丒Z+Y丒Z)+Y丒Z=X丒XOR(Y,Z)+Y丒Z偲偱偒傞偺偱丄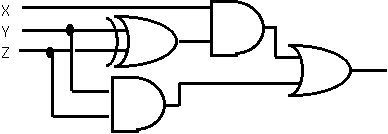 幚偼偦偺傎偐偵傕怓乆偱偒傞丅
幚偼偦偺傎偐偵傕怓乆偱偒傞丅




 偙偙偱丄愙抧晹偺夞楬偼徣偄偨丅師恾偼
偙偙偱丄愙抧晹偺夞楬偼徣偄偨丅師恾偼 丠丠丠
丠丠丠
 偙偺忬懺偱丄僗僀僢僠傪暵偠傞丅偡傞偲恀傫拞偺p敿摫懱晹偵儂乕儖偑嫙媼偝傟傞丅僀儊乕僕偲偟偰偼壓偺抂巕晅嬤偵儂乕儖偑弌偰偔傞丅僄儈僢僞傪偱偨揹巕偺堦晹偼偙偺嫙媼偝傟偨儂乕儖偲寢崌偟偰柍偔側傞偑丄戝晹暘偼嵍傊棳傟傞丅偙偆偟偰丄儀乕僗偵揹埑偑偐偐傞乮僾儔僗乯偲僐儗僋僞偐傜僄儈僢僞偵揹棳偑側偑傟傞偲偄偆丄夞楬偑偱偒偁偑傞丅偙傟傪壓偺恾}偺傛偆偵夞楬恾偲偡傞丅揹棳偺曽岦偲揹巕偺堏摦曽岦偼媡丅
偙偺忬懺偱丄僗僀僢僠傪暵偠傞丅偡傞偲恀傫拞偺p敿摫懱晹偵儂乕儖偑嫙媼偝傟傞丅僀儊乕僕偲偟偰偼壓偺抂巕晅嬤偵儂乕儖偑弌偰偔傞丅僄儈僢僞傪偱偨揹巕偺堦晹偼偙偺嫙媼偝傟偨儂乕儖偲寢崌偟偰柍偔側傞偑丄戝晹暘偼嵍傊棳傟傞丅偙偆偟偰丄儀乕僗偵揹埑偑偐偐傞乮僾儔僗乯偲僐儗僋僞偐傜僄儈僢僞偵揹棳偑側偑傟傞偲偄偆丄夞楬偑偱偒偁偑傞丅偙傟傪壓偺恾}偺傛偆偵夞楬恾偲偡傞丅揹棳偺曽岦偲揹巕偺堏摦曽岦偼媡丅

 偩傟偑B傪墴偡偐傪僩儔儞僕僗僞偵抲偒姺偊偨丄弌椡偼C偱偁傞丅
偩傟偑B傪墴偡偐傪僩儔儞僕僗僞偵抲偒姺偊偨丄弌椡偼C偱偁傞丅
 傑偢僩儔儞僕僗僞傪巊偭偰NOT夞楬傪嶌傞丅
傑偢僩儔儞僕僗僞傪巊偭偰NOT夞楬傪嶌傞丅
 http://lib1.nippon-foundation.or.jp/1998/0149/mokuji.htm
http://lib1.nippon-foundation.or.jp/1998/0149/mokuji.htm

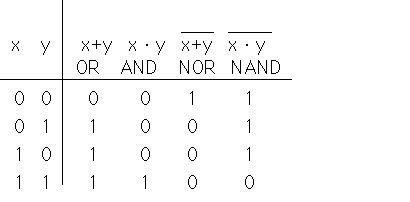
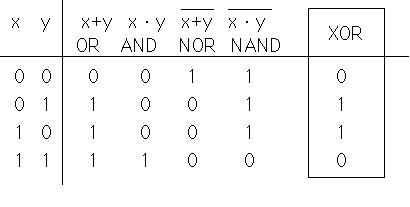

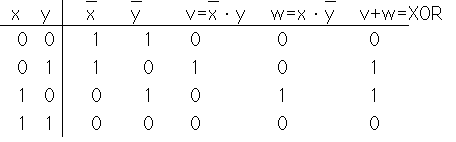
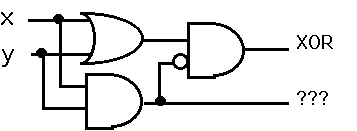
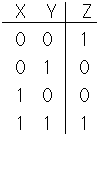
 偱偁傞丅傑偨偙偺恀棟昞傪昞偡BOOL戙悢幃偼Z=X丒Y+X丒Y偱偁傞偙偲傛傝丄師偺夞楬傕夝偱偁傞偙偲偑敾傞丅
偱偁傞丅傑偨偙偺恀棟昞傪昞偡BOOL戙悢幃偼Z=X丒Y+X丒Y偱偁傞偙偲傛傝丄師偺夞楬傕夝偱偁傞偙偲偑敾傞丅
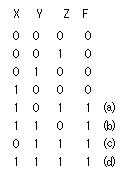 偒傟偄偱偼柍偄夞楬偱傑偢嶌傞丅呟呠呡呣偺偦傟偧傟偺応崌偺夞楬傪嶌傝OR傪庢傟偽傛偄偺偱丄
偒傟偄偱偼柍偄夞楬偱傑偢嶌傞丅呟呠呡呣偺偦傟偧傟偺応崌偺夞楬傪嶌傝OR傪庢傟偽傛偄偺偱丄 Bool戙悢偱偼丄F=X丒Y丒Z+X丒Y丒Z+X丒Y丒Z+X丒Y丒Z
Bool戙悢偱偼丄F=X丒Y丒Z+X丒Y丒Z+X丒Y丒Z+X丒Y丒Z 幚偼偦偺傎偐偵傕怓乆偱偒傞丅
幚偼偦偺傎偐偵傕怓乆偱偒傞丅