竹下徹の応用電磁気学II-2002　第六回

6計算回路ー加算回路

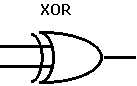
論理回路による加算回路:XORの利用いよいよ計算機らしい作業をおこなわせる回路である。すなわち　　１桁の足し算を考えよう。
0(2)+0(2)=0(2) ：これは２進数のゼロ　0(2)と0(2)を加えると、２進数でゼロになるという式である。同様に

0(2)+0(2)=00(2)
0(2)+1(2)=01(2)
1(2)+0(2)=01(2)
1(2)+1(2)=10(2) 最後の式は２進数の1、　1(2)と1(2)を加えると、２進数で10(2)になるという式である。この一桁目だけをみると、XOR回路の出力と同等である事が判る。よって、加算回路の各桁(i)は次のように描くことができる。fi=XOR(xi,yi),ki=AND(xi,yi) これをハーフアダーHalfAdder=HAと呼ぶ。HAは２入力２出力の素子である。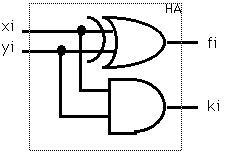

FullAdder(FA)の作り方一般の桁の加算回路はどうなるだろうか？
これはHAでは記述できない。なぜなら一つ下の桁からの桁上がりが有り、これを考慮し無ければならない。そこで、３入力の素子を考える。出力は２つである。これを満たす回路をフルアダーFullAdder と呼ぶ。これを実現する方法を２つ示す。（１）結果が１になるところをすべて構成しそのすべてのORを取る。
fiが１になるのは、(xi,yi,ki-1)の組み合わせで、(0,0,1), (0,1,0),(1,0,0)と(1,1,1)の４通りである。３入力の素子で(0,0,1)の時にのみ　出力1を作るには、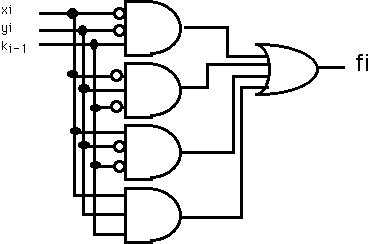但し、ここで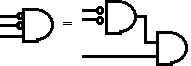という、３入力の素子を２入力素子２つから作った。入力側にある○はinaverter あるいはNOT回路を示す。

（１）の方法でkiが１になるのは、(xi,yi,ki-1)の組み合わせで、(0,1,1), (1,1,0),(1,0,1)と(1,1,1)の４通りである。同様にして作ろう。

（２）もっとかしこい方法：これはHA１個では記述できない。なぜなら一つ下の桁からの桁上がりが有り、これを考慮し無ければならない。そこで、３入力の素子を考える。
出力は２つである。一つ前の方法は万能であるが、汚い！スマートな方法は、HA(Half Adder）を使うことを考える、なにしろ１桁目はうまく行くので、まず、各桁の数値の和をHAでとる。出力は、さらに前の桁から上がってきたKi-1ともう一回和をHAで取る、残り、一つ目のHA-1のKiと二つ目の　HA-2のKiが余っているこれは、双方とも桁上がりで、どちらが上がっても結果の桁上がりが発生するからORを取ればよい。普通の２進法の演算を考える、10(2)+11(2)。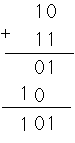あるいは11(2)+01(2)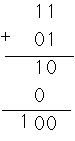：という例で示される通りだ。よって回路は次の図となる。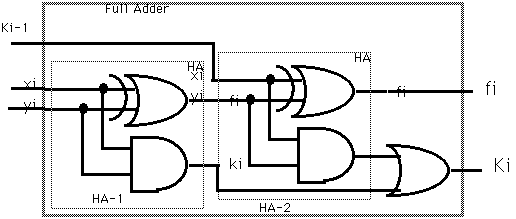一般の複数桁の加算回路はどうなるだろうか？
普通の複数桁の２進法の演算を考える、101(2)+111(2)=5(10)+7(10)=12(10)=1100(2)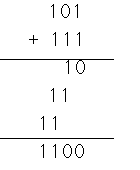

例えばこれをFAで実現するには、各桁に１個のFAを配置し
x+y=z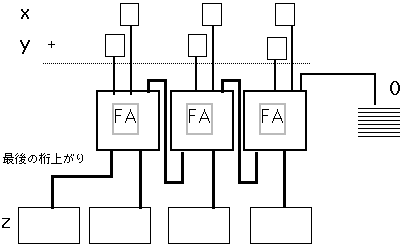

問題：ある５桁の計算でFAをすべてXORとORで書き下し、その値（ブール代数値）を示せ。