竹下徹の応用電磁気学II-2002 第七回
7計算回路ー減算回路
減算には補数を使う
さて足し算(和、加算)できたら、引き算(差、減算)ですね、
これには「負の数」に当たる「補数」を定義し使います。
話の筋として、10進法でまず考えましょう。
4082-643=4082+(9999-0643)+1 -10000
=3439 という演算が成り立ちます。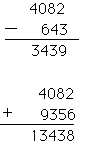
一般に10進数xとyの引き算x-y=x+(10n-1-y)-10n+1と書くこと
に対応します。nは桁数出、xや yの桁より大きければ何でも良い。
ここでカッコ内が補数の定義です。すなわち643の4桁の補数は
(9999-0643)=9356
であるという、これは9999は4桁の数値で最大のものです、これ
からどんな数を引いても正の整数となります。例えば3の一桁の補数は9-3=6で
6となります。
これを二進数に当てはめて補数を定義してみると、一桁の数0の補数は、1-0=1、
もう一つの可能性である、一桁の数1の補数は、1-1=0、となります。
(10進数では何のことかよくわからなかったでしょうが)二進数では、その意味は明らかですね、二進数の補数とは0->1,1->0と
いう対応関係からNOTを取ればよいことが。。。すなわち二進数x(2)とy(2)の引き算は次のように書けます。
x(2)-y(2)=x(2)+{y(2)の補数}-10n+1
=x(2)+{y(2)}-10n+1
これを例で示します。10進数で11-5=6を二進数でかくと、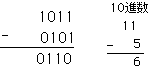
これを上の式を使って、
1011+(0101)+1-最上位の桁を落とす=1011+1010
=10101+1-最上位の桁を落とす=10110-最上位の桁を落とす=0110
すなわち負の数を補数+1で定義したとも言えましょう。二進数4桁で表を作ります
10進数 2進数 ー10進数 -2進数
0 0000 0 0000
1 0001 -1 1111
2 0010 -2 1110
3 0011 -3 1101
4 0100 -4 1100
5 0101 -5 1011
6 0110 -6 1010
7 0111 -7 1001
8 1000 -8 1000
一般の複数桁の減算回路はどうなるだろうか?
減算を補数を使って加算で実行できることを学んだ。
つまり2進数の補数はNOT回路により作られるので、
これを用いて加算回路FAに少々の変更を加えて次の回路を
考えよう。二進数x(2)とy(2)の差を取る計算は、
z(2)=x(2)-y(2)=
x(2)+(y(2))+1-最上位の桁を落とす
という作業で実現されるので、
これをFAで実現するには、各桁に1個のFAを配置し
x+y=z
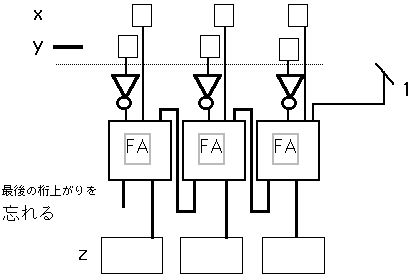 FullAdder(FA)による減算回路が実現できる・
FullAdder(FA)による減算回路が実現できる・
加算回路が次で有ったことを思い出すと、
x+y=z
両者はそっくりであることが判る。では両者を合体させてみよう。要は、x+y=zを実行するとき加算(+)の時はyの信号はそのままFA
(FullAdder)へ入ればよいし、減算(-)の時はyの信号にNOTをとおしてinvertすればよい。加算か減算かを表す符号(s)を1ビット作
り、これをs=1:減算、s=0:加算と定義しよう。s=1のとき入力にNOTを付け、s=0のときに 入力に何もしない回路を考えればよい。つまり真理
表では
これを満たす回路はXORであることが解る、よって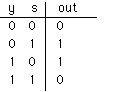
下の回路がそれを満たす。さらに最下位ビットの
処理も減算では1加えるし、加算では0を加えヲるの
でSをそのまま持ってくればよい。最後に最上位ビット
の桁上がりの処理は、下図でうまく行く事を確かめよ。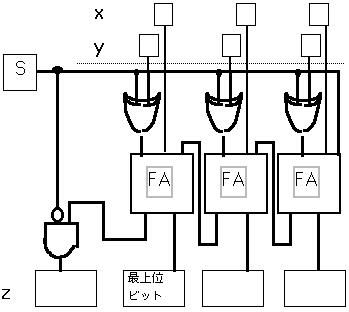 こ
れがFullAdder
(FA)による加減算回路である。
こ
れがFullAdder
(FA)による加減算回路である。
ここで各桁のカッコの中に入っている0 か1の値の働きを述べる。
全世界の計算機が共通の内部表現で文字や数字を表さない限り通信不可能である。
コンピュータの内部のメモリにおのおのの文字や数字は0か1のビットとして格納されているので、1ビットまで共通であることが要求される。それがコン
ピュータがまだ作りはめられた頃に決められたアAスキーascii規格である。ASCII
(American Standard Code for Information
Interchange)英数字を表す7ビット・コードで、1963年に
ANSI 規格になった。27=128種の文
字を表現でき、英数字の世界では一応十分とされる規格である。うち94文字は印刷可能で有り、残り34文字は制御コード(CTRLやESC等)である。た
だし、漢字などは含まず、アルファベットや数字、特殊文字だけである。ASCIIは
ISO(国際標準化機構)で国際規格(ISO646)として制定された。
ここでは8ビットデータを16進表記(Hexadesimal)と2進法表記で書いた
00=0000 0000 には何もアサインされていない。
....
0A=0000 1010 = LF 改行コード line feed
0B=0000 1101 = CR 改行コード carriage return
....
30=0011 0000 = 0 数字のゼロ
31=0011 0001 = 1 数字の1
....
39=0011 1001 = 9 数字の9
....
41=0100 0001 = A アルファベット大文字のA
42=0100 0010 = B アルファベット大文字のB
43=0100 0011 = C アルファベット大文字のC
...
52=0101 1010 = Z アルファベット大文字のZ
....
61=0110 0001 = a アルファベット小文字のa
62=0110 0010 = b アルファベット小文字のb
63=0110 0011 = c アルファベット小文字のc
...
7A=0111 1010 = z アルファベット小文字のz
...
80=1000 0000 より先は8ビットデfータである。
ISO 646 (または SACII)を 8 ビットに拡張し、
0x80〜0xFFに文字を追加しようという考え方が生まれます。その一つが、これもおな
じみの JIS カタカナです。前述の JIS X0201 の左半分(0x00〜0x7F)は ISO 646
日本版で、右半分(0x80〜0xFF)は日本独規格のフカタカナというわけです。その他の国々でも同様におれがおれがと言って勝手な拡張をしました。そ
の結果8ビットめは全く互換性のないものとなりました。それだけなら被害は少ないのですが、、、、
コンピュータ内の数値の表現の統一規格 ISO8266
ASCII(7ビット)では128種の文字しか扱うことができない。漢字の場合は 16ビット
規格(2バイト)があります。2^16=65536
これだけあれば通常は大丈夫です。
JIS規格として、第一水準=2965字、 第二水準=3388字 @が決められています。例えば、次のようになっています。16進表現です。
愛=3026 知=434F 学=3358 院=3121 大=4267(いずれもJIS規格)。
では計算機の内部表現で数値をどうやって表しているか。
ビット(bit)ということばは、「2進法のひと桁」 (binary digit)
整数の場合は通常先頭の1ビットを符号ビットにふり、残りで整数を表します。例えば4ビットの整数では正の整数は
0から7まで、負の整数は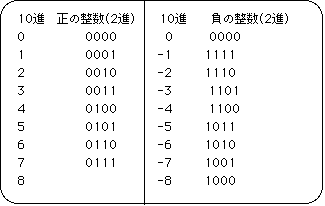
0からー8までの合計15個(3ビットですから)を表現できます。右と左を足して1引くとつまり補数関係を要求すると、一桁桁上繧ェり残り全てのビットが
クリアされることが判りますね。32ビットではどうでしょうか?
では実数はどうするか?少数点以下の値も含んだ数値を表す場合には、指数方式または
浮動少数点と呼ばれる表現を使うのが普通です。つまり指数部と仮数部に分けて実数を扱うことにします。10進数では3.14=3*10^0+1*10^
(-1)+4*10^(-2)=0.314*10^(-1)と書かれ、この最後の
0.314を仮数、10^-1の-1を指数と呼びます。これを2進数に置き換えて同じように
0.25(10) = 0*2^0+0*2^(-1)+1*2^(-2) = 0.01(2)
3.625 (10)= 2+1+0.5+0.125 = 1*2^1+1*2^0+1*2^(-1)+0*2^(-2)+1*2^(-3
)= 11.101(2)
という表現が可能である。ここでは割り切れる(2^nで表現できる物を使った) で
は実数はどうするか?少数点以下の値も含んだ数値を表す場合には、
で
は実数はどうするか?少数点以下の値も含んだ数値を表す場合には、
整数に対しては,次の例のように,与えられた10進数を2で順に割っていき,各割り算における余りを求めるという方法がよく使われます。
実数に対しては,次の例のように,2を順に乗じていき,その1の桁を・進数として採用していく方法があります。
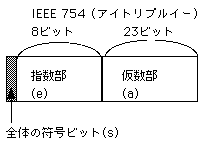 仮数部は23ビットの有限ビット数なので、当然有限な数(実数)しか現すこ
とができま
せん。(0.abcd...)(2)という二進数小数点以下の数値は(非規格化表現)
仮数部は23ビットの有限ビット数なので、当然有限な数(実数)しか現すこ
とができま
せん。(0.abcd...)(2)という二進数小数点以下の数値は(非規格化表現)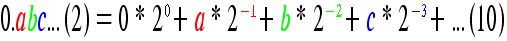 を
現します。従って二進数小
数点以下の数を10進数に変換することは簡単です。反対に10進数2を二進数に変換するには、次ぎような作業が適切でしょう。たとえば
を
現します。従って二進数小
数点以下の数を10進数に変換することは簡単です。反対に10進数2を二進数に変換するには、次ぎような作業が適切でしょう。たとえば
仮数部の例:10進数0.1を2進数へ変換
0.1×2=0.2 ・・・ 0
<<<10進数0.1に2を掛けます。でもまだ桁上がりがないので、小数の上の0を取ります。
0.2×2=0.4 ・・・ 0
<<<10進数0.1に2を掛けます。でもまだ桁上がりがないので、小数の上の0を取ります。
0.4×2=0.8 ・・・ 0
<<<10進数0.1に2を掛けます。でもまだ桁上がりがないので、小数の上の0を取ります。
0.8×2=1.6 ・・・ 1
<<<10進数0.1に2を掛けます。桁上がりが起こったので、小数の上の1を取ります。さらに1を引いて0.6を相手ににしておなじ事を繰り返します
0.6×2=1.2 ・・・ 1
0.2×2=0.4 ・・・ 0
・・・・・
(0.1)(10)=(0.00011001100110011001100110011...)(2)
<<<この二進数がどの程度10進0.1に近いか調べてください。本当は循環2進少数です。どこかで止めると当然0.1
(10)とは異なる値をしめします、どのくらい違うかが問題ですが、、さらに必ず小さな値になります、何しろ切り捨てたのですから、、小数点以下23桁
(2進数で)のみ使うと
(0.00011001100110011001100)(2)
=0.099999905(10)となり1x10の(ー6)乗小さくなります。
この例からも明らかなように、10進数における小数を2進数に変換すると循環小数(2)になってしまうような場合が起こります。データをコンピュータ
に記憶させる場合,必ず2進数に変換されます。また、コンピュータに記憶できる桁数には制限があります。従って、循環小数になってしまうような場合、途中
で打ち切らざるを得ません。つまり、上の例の場合、10進数のフ0.1とコンピュータが内部に記憶している0.1に対応する数字は等しくないことになりま
す。
(0.1)(10)=(0.000110)(2) この場合仮数は0000110(7bit表示)、指数は0を使う。
= は正確には一致しないことに注意。
(0.000110)(2)=2^(-4)+2^(-5)=0.0625+0.03125= 0.09375 ,
2^(1)=2の(1)乗の意味である。
一般に仮数部のビット並びをaとし、指数部をe、全体符号をsとすると、これは
実数 (-1)^s×[0.a](2)×2^{[e](10)−127}
を表わす。但しeが8ビットの時を考えている。よって、-128
≦ e(10)-127 < 2^7-1=127なので、このとき、同様にaは23ビット(実は先頭を含めて24ビット)有効桁数は
(24ビット)=2^24=16777216=10進7.2桁である。また
指数部は 2^128=3.4x10^38
で10進数で10^±38まで扱う事ができる。ちなみに[0.a](2)の部分は非規格化とよばれこれ以外に[1.a](2) として扱う
規格化という形
式が存在するので要注意。ここでは簡単のため非規格化を用いた。
例えば小数の0.101(2)は
0.101(2)=
0×2^0 + 1×2^(-1) + 0×2^(-2) +
1×2^(-3)=0+0.5+0+0.125=0.675(10)
なので,0.625(10)となる.ところが,0.6(10)を2進数で表わそうとすると,困ったことになる.それは,何桁つかってもちょうど0.6
(10)にすることが出来ないのである.
0.6(10)=0.10011001100110011001100110011001100110011....(2)
このことから,10進数の小数は2進数で表わせない場合があることが判る.コンピュータでは無限に桁数を増やすことが出来ないので,何桁かで打ち切るしか
ない.このとき生じる誤差を丸め誤差と呼ぶ.コンピュータにはつきものの困った問題である。
非規格化の場合の内部表現(IEEE754) 小数点以下を0.abcdef...
と表す。 <<<わかりやすい。
float x=6.0(10);
x = 0 10000010 11000000000000000000000
float y=-0.375(10);
y = 1 01111110 11000000000000000000000
規格化の場合の内部表現(IEEE754) 小数点以下を1.abcdef...
とずらして表す。<<<<こっちが UNIXの計算機ではつかわれている。IEEE754である。
float x=6.0(10); = (+1)*110.0 0000 0000 0000 0000 0000 (2)
= (+1)*(2**2)*(1.100 0000 0000 0000 0000 0000) 指数部e = 2+127
=129 よりe=1000 0001 となる、従って
x = 0 10000001 10000000000000000000000
float y=-0.375(10); (-1)*0.011 0000 0000 0000 0000 0000 (2)
= (11)*(2**-2)*(1.100 0000 0000 0000 0000 0000) 指数部e = -2+127
=125 よりe=0111 1101 となる、従って
y = 1 01111101 10000000000000000000000
float x=0.1(10): 0 01111011 10011001100110011001101(2)と書かれる。
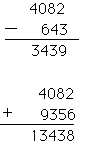
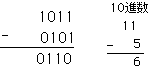
 FullAdder(FA)による減算回路が実現できる・
FullAdder(FA)による減算回路が実現できる・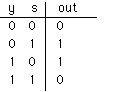
 こ
れがFullAdder
(FA)による加減算回路である。
こ
れがFullAdder
(FA)による加減算回路である。
 で
は実数はどうするか?少数点以下の値も含んだ数値を表す場合には、
で
は実数はどうするか?少数点以下の値も含んだ数値を表す場合には、 仮数部は23ビットの有限ビット数なので、当然有限な数(実数)しか現すこ
とができま
せん。(0.abcd...)(2)という二進数小数点以下の数値は(非規格化表現)
仮数部は23ビットの有限ビット数なので、当然有限な数(実数)しか現すこ
とができま
せん。(0.abcd...)(2)という二進数小数点以下の数値は(非規格化表現)