Untitled Document

物理実験学

竹下徹　(05082004)

1.実験とは
導入

自然の理解＝物理学の目的<----- 理論　　　　　両輪
　　　　　　　　　　　　<----- 実験

理論：概念・思想
方程式で表現　<-----> 　数値：実験
　　　　　　｜　　　　　　　　　｜　｜
　　　　予言　 ---------->>> 検証　｜
　　　　　　　　　　　　　　　　　　｜
理論の変更あるいは破棄 <------------ 新発見
　　　　　　　　例１：マイケルソンモーレーの実験
　　　　　　　　　　　--->　アインシュタインの光速度不変の原理

　　　　　　　　例２：　ティコブラーエ測定データー＞ケプラーの３法則
　　　　　　　　　　　---> ニュートン唐ﾌ万有引力の法則
　　　　　　　　　　　予言：　　海王星の存在

実験とは　　　　　　　実験の再現性: 　同じ実験をやれば同じ結果がえられる
　　　　　　　　　　　　　　（同じが問題である：有限精度なので）
　　　　　　　　万人が認めることができる
　　　　　　　　　　　数値ーデータ　：　　実数　＜＜＜　精度　：　誤差
この授業の目的
　　　　　　　　　　　　　　　ここの部分を考える
　　　実験の実行：ーー複数の数値データーー＞結果　ーー＞結論
　　後期以降の物理学実験I,II,IIIで実際使う！
　　　関数電卓を使用した授業となるが、データ処理が複雑になると、
　　　電卓では手に終えなくなる。パソコンを使ったデータ処理も別の授業あるいは、自分で学べ。

１年生向けメッセージ：大学は、本来自ら学び掘り下げて行く所である。待っていては指事はこない、こないのは、何もしなくてもいいってことじゃない！自分で考え、押し進めてて行く事を、回りは仮定している。高校では、大学を目標に問題を解いていれば良かったのではないか？　大学ではすべて（授業も、生活も）に渡って自分で考え行動することを求められている。授業では、先生を使え、聞け！ただし質問を考えるのは君だ！ただしこの授業では、なんとか、自分で始める癖をつけるようにしむけたい。

単位：試験２回＋授業中の宿題：ちゃんと勉強しないと単位はない、大学では絶対評価である。

データとは
　　　測定・実験結果あるいは途中に現れる数値
　　　一般に数値ーデータは　実数　で　　精度　を持つ　　：　誤差と呼ぶ人もいるが。
観測や測定から得られる：ーーー整数型　不連続量：例コイントス実験：ここでは精度がない。
　　　　　　　　　　　ーーーー実数型　連続量：　例：長さの測定実験：精度が問題。

データの視覚化

整数型データ：４回のコイントスで、H,T,T,Tと出たとしよう、ここで何回「でたか」に興味があるときは、棒グラフを描く

実数型データ：みなさんの身長、１人１人のデータではなく、その全体像！に興味があるとき、　　ヒストグラムを描く：bin bindingの問題:有限精度を考慮：たとえば、1mmまで目盛ってある物差をつかって身長をはかった場合、細小目盛りの1/10まで読み取れると通常する。例：173.44cmここで実数値といえども有限精度である。
173.435より大きく173.445より小さい範囲にある時である。この幅を考慮したbindingが図の上から中である、下は全体をみわたすとき便利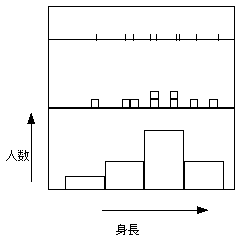

データの代表値は
　　　　　　　　　　　数値ーデータ　：　　実数
同じ質の複数のデータ（データの組み）の代表値

実数型データ：たとえばみなさんの身長で、１人１人のデータではなく、代表値を一つあげよ、という場合どうするか？図で、一番上ではみんな平等（横幅大変小さい）にしたので、代表をだせない。（一番高い（あるいは低い）のが代表できるか？）

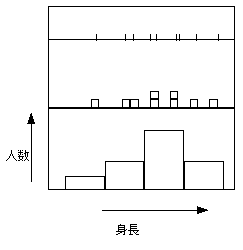
図の下側ように横幅を考慮してまとめると、２つぐらい代表値の取り方が考えられる。
（１）一番高いビンをその代表値とする。（これじゃ、ここのデータの値をあまり考慮してない）
（２）平均をとる

平均：n個のデータのとき、
　　　　　データをxi (i=1,,,,n) について　　x=(x1+x2+...+xn)/n
　　　　　=S(xi)/n
を算術平均と呼ぶ。

平均は算術平均が全てではないのだ！

重み付き平均：上の平均は或いは算術平均は重み付き平均の特殊な場合である、つまり各データに重みが付与されているような場合でこれをwiとしよう。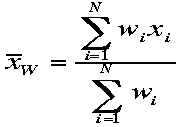この式で定義する平均を重み付き平均と呼ぶ。例えば１アンペアが最小目盛りの電流計で読んだ値と0.1アンペアまで読める電流計の結果の平均値を求めよと言われたとき、両者は同一に扱う理由はない。0.1アンペアまで読める電流計の結果を尊重し大きな重みを加えるべきであると判断すればこれを用いる。

調和平均：　　xchouwa=n/(1/x1+1/x2+....+1/xn)
平均の速さはこれ。つまり距離L(m) 離れた二点AとBがあり、AからB へ行くときは一定の速さv1(m/s)で歩き、帰る時BからAへは、一定の速さ v2(m/s)で歩いたとしよう。このとき往復の平均の速さはいくらか？そもそも速さは移動距離をそれに要した時間で割った二次的な物理量なので単純な算術平均ではだめなのだ。行きに架かる時間t1=L/v1であり、帰りに要する時間t2=L/v2である、従って平均の速さV=2L/(t1+t2)=2/ (1/v1+1/v2)となり調和平均の式なる。
相乗平均：
xsoujyou=(x1x2....xn)1/n 1/n乗根
各年の生産高の年平均なん倍になりましたか？はこれ

２乗平均
　xrms=sqrt((x12+x22+...xn2)/n)

注意：平均値の単位はかならず、データの単位と同じ。物理学では数値は必ず、単位を持ち意味を持つ。
平均値は複数の数値データの代表値である、従って、同じ単位をもつべし、
さらにi番目のデータが別の順番で現れても結果は同じはずであり、入れ替えに関して対称であるべきである。その意味で上記、算術平均、調和平均、相乗平均、重み付き平均は全てこの条件を満たす。どの数値の場合どの平均を取るべきかは、数値の出所による。例えば、抵抗の並列つなぎの計算は調和平均だし、増倍率などの平均は相乗平均を取るべきである。また重み付き平均は、この授業で最も重要で後に議論する。
何かの長さをはかれ、図を描け、代表値を出せ。物差を持たない者は工夫せよ。
例：　　ある高さから物体を落下させ、gをを測定する。
　　　　　　h=gt2/2 :これを理論として、検証できるか？
　　　　　　　g=2h/t2 : hとtを測定すればよいはず。
関数電卓を入手してください！今後この授業そして、実験で必ず使います。
　　　　　　乱数発生のできる機能付き物が望ましい。
ここまでの宿題：ものの長さを測れ。

レポート例：「ものの長さを測る」

A4様紙の横（短い方向）の長さを測定する。

測定は、同じ紙の同じ程度の位置にて複数回おこなう。そのさい、物差しはその都度いったん紙から離す。物差しの最小メモリは1mm.

方法１：ゼロ点を合わせて、長さを読む。
方法２：任意の位置に物差しを置きｫ、長さは位置の差で計算する。

方法１：データ　　　　　　　　　　方法2：データ
回数　　　　長さ（ｃｍ）　　　　左の位置読み　　右位置読み　　長さ（ｃｍ）
1　　　　　　　20.97　　　　　　　4.16　　　　　25.14　　　　20.98
2　　　　　　　20.99　　　　　　　0.80　　　　　21.79　　　　20.99
3　　　　　　　20.98　　　　　　　3.92　　　　　24.41　　　　20.49
4　　　　　　　20.98　　　　　　　1.32　　　　　22.32　　　　21.00
5　　　　　　　20.99　　　　　　　6.94　　　　　27.93　　　　20.99
6　　　　　　　21.00　　　　　　　3.58　　　　　24.56　　　　20.98
7　　　　　　　21.02　　　　　　　2.49　　　　　23.48　　　　20.99
8　　　　　　　20.99　　　　　　　4.91　　　　　25.90　　　　20.99
9　　　　　　　20.98　　　　　　　5.03　　　　　26.02　　　　20.99

平均値　　20.989= 20.99 cm 20.989=20.99cm（３番目のデータなし）
標準偏差　0.015　= 0.02cm 0.007 = 0.01cm
結果：両者は同等で、長さは、20.99ｃｍである。

データの図式化。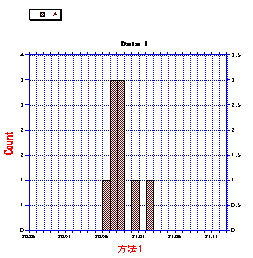

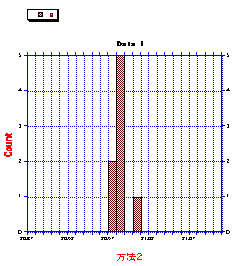
複数の数値データの広がりをあらわす量

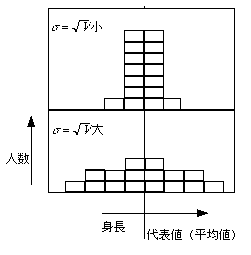
右図は同じ代表値（平均値）の２つの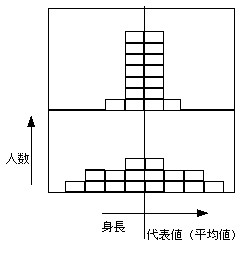
　　分布だが
同じではない！
違い＝（分布の）ひろがりをあらわす量を考えよう！

平均：n個のデータのとき、
　　　　　データをxi (i=1,,,,n) について　　を平均と呼ぶ。
「ひろがり」をあらわす量として
平均値からのずれ（差）を足しあげればよい！
がしかし
は不適切である。
なぜなら

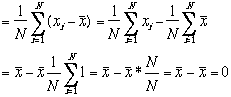
新しい量を考える。

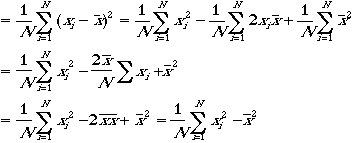
これをVariance　分散　と呼ぶ　　

また標準偏差　を　　　と定義する。分散の平方根として定義する。

複数の数値データの広がりをあらわす量（その２）

平均値：

分散：=

skew:

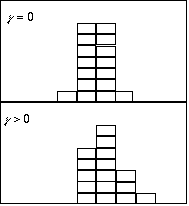
skewはdimensionless 無次元量
代表値の周りの分布の広がりの左右非対称度を示す。

(x-x)r は代表値の周りのモーメントという、
r=1: を力学の言葉では重心である、
r=2:　は　力学では、慣性モーメントと呼ぶ。

2つの量の間の関係：複数の数値データの組み(xi,yi)の扱い
今までのデータは、一つの数値(xi) を測定した場合
であった、　　２つのデータの組み(xi,yi)を測定
する場合を考えよう。たとえば、xi=ある人の身長、yi=その人の体重。この場合iは人が同じであることを表し、xiとyjは本来無関係である。
これらのデータの組みを　{(x1,y1),(x2,y2),......(xN,yN)}　と表す。
ここで

例えば、身長と体重などの量のように関係が
推測されるものがある、これを次のように定義し
導入する。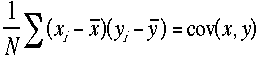ここで

cov(x,y)の単位は、xの単位かけyの単位
である。つまり、無次元量ではない。それも妙な単位である（例の身長＝x、体重＝yの場合、
covの単位はm＊kgとなり、物理量として意味を持たない。）こういう時は、無次元量にしてしまう方がよい。
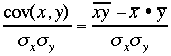これを相関係数と呼ぶ。
この量は無次元量で、-1から１の間にある。

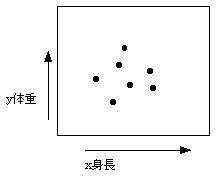
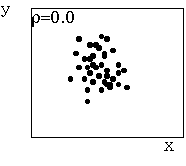
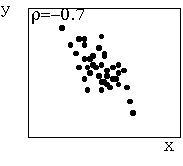
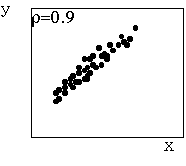
問題：身の回りの関係のありそうな２つの量をさがし、両者の関係を議論せよ。

物理実験学　　 10/April/2003 質問表まとめ

　正しい字：離散、幅、頻度

質問：「最小目盛りの1/10まで読めというのはなぜか？」
答え：　確かに目分量になります、それでもその数値をいくらといくらの間と答えたのでは答えになりません、また中間をとって xxx.5としても違いますよね！それで無理矢理1/10まで読んで下さい。これが物理学を実験する上で常識です。その結果をどう考えるかは次回はなします。

質問：「ヒストグラムのビン幅は、何を基準に決めるのか」
答え：　　ヒストグラムはデータの全体像を把握するための視覚化を行います。ですから全体像が見えるようにビン幅を決めます。一般にデータ全体を１０個程度のビンに分けるのが全体像を見えやすくします。

「質問：なぜ実数は連続量というのか？」
答え：　　実数は小数点以下無限の数値がつながった存在です、ですからその数値よりほんの少し大きな別の実数、あるいはほんの少し小さな別の実数が存在し、実軸上を無限に覆い尽くしています。　例えばあるものの長さをいくらか、という問いに対して、答えは本当の長さは無限に精度が良ければ無限に数値がならんで長さはこれこれというべきでしょう、その意味で我々は実数を相手にしています。

質問：「ありません」
答え：　　それでも質問をひねり出すのが質問票ですので、無理してください。

物理実験学　　 17/April/2003 質問表まとめ

　正しい字：

質問：「どうしてたくさんの平均の取り方が存在するのか？」
答え：　それは対象とする物理量にいろいろな単位を持った種類があるからです。調和平均の場合について次に述べます。

質問：「調和平均とは？」
答え：F　調和平均の式は次のような場合に現れます。それは距離がL(m)はなれた２点A,Bについて、行き(AｮB)は平均の速さV1(m/s)で歩き、帰り(BｮA)は平均の速さV2(m/s)で歩いたとしましょう、さて平均の速さはいくらでしょう？。というとき、と答えますか？　歩いた距離をかかった時間で割った価が平均の速さですから、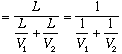ってものでしょう！V1,V2をx1,x2に置きかえると理解しやすいですか？このように関係する物理量の持つ単位などにより計算は適切に行われなければなりません。

「質問：三乗平均を計算刷るのはなぜか？」
答え：二乗平均でたしかにデータの分布の拡がりを表すパラメータを計算刷ることができました。しかしこのﾌときは二乗を取ったので、算術平均の値の左右に対称に距離だけを計算しています、左は左だえで足しあげるには符合を不可しなければ鳴りません、こういうとき三乗が役立ちます。つまり、左右非対称な分布の拡がりを表すことのできる量が三乗平均（スキュー）です。私のノートをｩてください。http://atlas.shinshu-u.ac.jp/

質問：「偏差値と標準偏差の違いはなにですか？」
答え：　偏差値をSi,標準偏差をsとすると、両者には次の関係があります。つまりあなたの得点xiと平均点*の距離（離れ具合）を標準偏差で割って１０倍し平均値を５０へずらした。偏差値５０の人は平均だ、偏差値６０の人は平均より１標準偏差ずれたところにいる！