ガウス分布の形を他の分布から導く
ガウス分布はどこで御利益があるか?
(1)物理で扱うデータの精度をあわらす量:次節 中心極限定理
他の物理問題:(2) ガウス分布関数 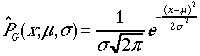 で
で
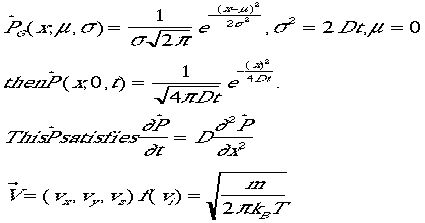
この方程式は拡散方程式である。
(3)温度Tの気体分子の速度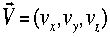 は次の分布(マックスウェル分布)に従うことが知られている。各成分はマックスウェル分布に従う。
は次の分布(マックスウェル分布)に従うことが知られている。各成分はマックスウェル分布に従う。
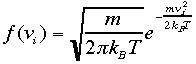 これは期待値
これは期待値 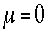 、 分散
、 分散 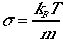 のガウス分布である。
のガウス分布である。
二項分布をガウス分布で近似することができる。
二項分布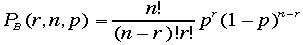 でnを大きく、かつ p=0.5付近に持ってくると左右対称の分布となる、またnは大きいので本来離散型の分布が連続的にみえてくる。これはガウス分布であろう。証明はちょっと難しい。
でnを大きく、かつ p=0.5付近に持ってくると左右対称の分布となる、またnは大きいので本来離散型の分布が連続的にみえてくる。これはガウス分布であろう。証明はちょっと難しい。
ポアソン分布とガウス分布を比べてみる。
ポアソン分布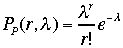 両辺の対数をとって
両辺の対数をとって
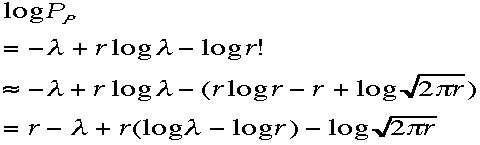 ここでは Starlingの式を用いて近似した。
ここでは Starlingの式を用いて近似した。
Starlingの式は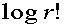 =
= 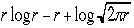 とかかれる。さらに
とかかれる。さらに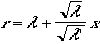 として、
として、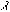 ,rは大きな量とし、相対的にx,
,rは大きな量とし、相対的にx,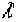 は同程度の大きさで相対的に
は同程度の大きさで相対的に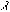 ,rに比べて小さな量である。従って、
,rに比べて小さな量である。従って、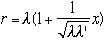 という式で
という式で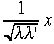 は1に比べて小さな量である。近似をするわけだ。
は1に比べて小さな量である。近似をするわけだ。
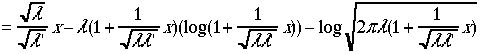 となる。
となる。
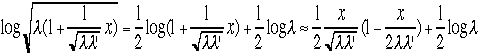 logのTayler展開式の2次までとる式をつかうと、
logのTayler展開式の2次までとる式をつかうと、
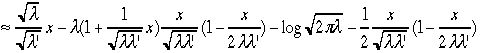 これを
これを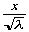 の2次の近似までとると、
の2次の近似までとると、
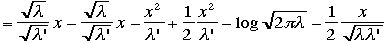 最終式は
最終式は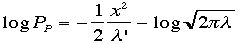 となる。ここで
となる。ここで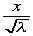 を小さいとして無視した。さらにPpという離散型ポアソン分布から連続型のガウス分布へ移行しようというのだから、積分系で書くことが確率となる。
を小さいとして無視した。さらにPpという離散型ポアソン分布から連続型のガウス分布へ移行しようというのだから、積分系で書くことが確率となる。
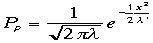 が確率密度で
が確率密度で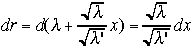 より、
より、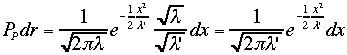 となり、最終的に大きな
となり、最終的に大きな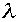 に依存しない形となる、ここでガウス分布の広がりを表す分散は
に依存しない形となる、ここでガウス分布の広がりを表す分散は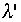 である。ちなみに期待値(平均値)はゼロの場合である、なにしろ大きなr、
である。ちなみに期待値(平均値)はゼロの場合である、なにしろ大きなr、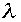 でポアソン分布はガウス分布に近いことを示したのであるから。
でポアソン分布はガウス分布に近いことを示したのであるから。
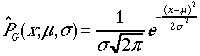 で
で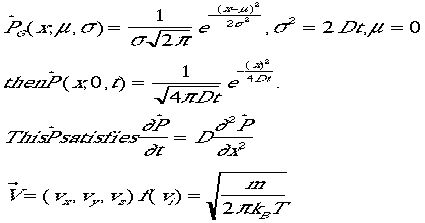
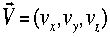 は次の分布(マックスウェル分布)に従うことが知られている。各成分はマックスウェル分布に従う。
は次の分布(マックスウェル分布)に従うことが知られている。各成分はマックスウェル分布に従う。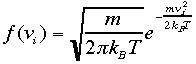 これは期待値
これは期待値 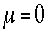 、 分散
、 分散 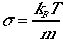 のガウス分布である。
のガウス分布である。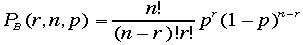 でnを大きく、かつ p=0.5付近に持ってくると左右対称の分布となる、またnは大きいので本来離散型の分布が連続的にみえてくる。これはガウス分布であろう。証明はちょっと難しい。
でnを大きく、かつ p=0.5付近に持ってくると左右対称の分布となる、またnは大きいので本来離散型の分布が連続的にみえてくる。これはガウス分布であろう。証明はちょっと難しい。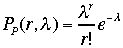 両辺の対数をとって
両辺の対数をとって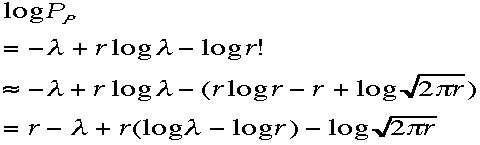 ここでは Starlingの式を用いて近似した。
ここでは Starlingの式を用いて近似した。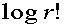 =
= 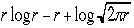 とかかれる。さらに
とかかれる。さらに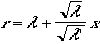 として、
として、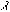 ,rは大きな量とし、相対的にx,
,rは大きな量とし、相対的にx,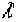 は同程度の大きさで相対的に
は同程度の大きさで相対的に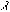 ,rに比べて小さな量である。従って、
,rに比べて小さな量である。従って、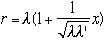 という式で
という式で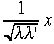 は1に比べて小さな量である。近似をするわけだ。
は1に比べて小さな量である。近似をするわけだ。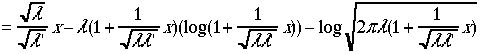 となる。
となる。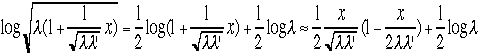 logのTayler展開式の2次までとる式をつかうと、
logのTayler展開式の2次までとる式をつかうと、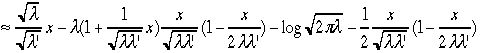 これを
これを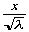 の2次の近似までとると、
の2次の近似までとると、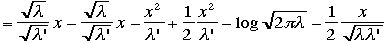 最終式は
最終式は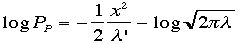 となる。ここで
となる。ここで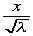 を小さいとして無視した。さらにPpという離散型ポアソン分布から連続型のガウス分布へ移行しようというのだから、積分系で書くことが確率となる。
を小さいとして無視した。さらにPpという離散型ポアソン分布から連続型のガウス分布へ移行しようというのだから、積分系で書くことが確率となる。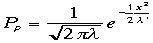 が確率密度で
が確率密度で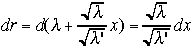 より、
より、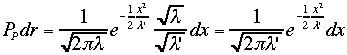 となり、最終的に大きな
となり、最終的に大きな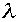 に依存しない形となる、ここでガウス分布の広がりを表す分散は
に依存しない形となる、ここでガウス分布の広がりを表す分散は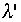 である。ちなみに期待値(平均値)はゼロの場合である、なにしろ大きなr、
である。ちなみに期待値(平均値)はゼロの場合である、なにしろ大きなr、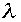 でポアソン分布はガウス分布に近いことを示したのであるから。
でポアソン分布はガウス分布に近いことを示したのであるから。