特性関数の導入：
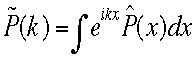として確率密度関数
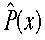のフーリエ変換として特性関数
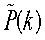を定義します。
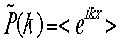であり特性関数はexp(ikx)の期待値とも言えます。また離散的な場合はつぎのように書きます。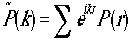
さて特性関数のｎ階微分を考えてください。そのうえk=0の点で計算すると，つぎの式を得ます。
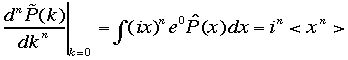これはxのｎ乗のモーメントを計算していることに他なりません。ここまでは準備です。変数x=x1+x2とかかれるとき、またx1は
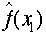,x2は
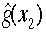という確率密度関数にしたがう時を考えましょう。このときxが従う確立密度関数
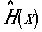はつぎの式になります。
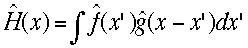なぜならx=x1+x2であり、全てのx1,x2の組みについて和を取るべきであり、これはx1,x2が連続量の時は積分で計算されます。これは convolutionと呼ばれます。これを特性関数をつかって書き直すと、
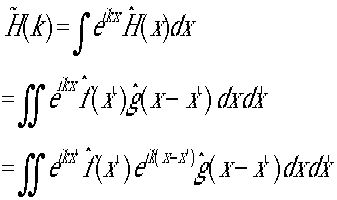となり、積分の dxをd(x-x')に置きかえると、
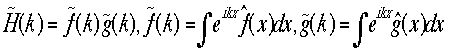とかけることがわかります。つまり二つの変数x1,x2の和の新しい確率変数x=x1+x2は特性関数がそれぞれの積で与えられることがわかります。一方Talyer展開から
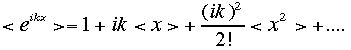とかかれます。両辺のlogを取ると、
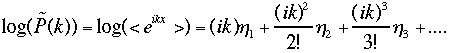ここでは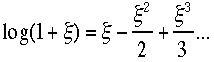
を使いました。
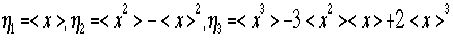.....各
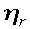はｘのr乗のオーダーの大きさである、またｘは小さいとTalyer展開したのを思い出してほしい。したがって xの三乗以上の小さな項を忘れると、つまりh1,h2だけでかける
。
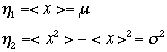と置きかえると、
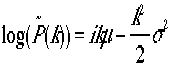と言う関係式をえる。すなわち
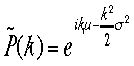であり、これは下で述べるガウス関数の特性関数である。一般にフーリエ変換は逆変換が存在し、つぎの関係がある。
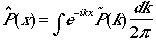
ガウス関数のとき、つまり
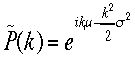ならば、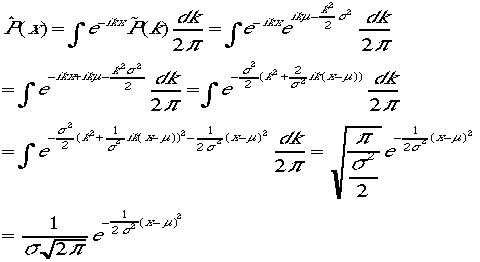
となりガウス関数が導かれる。ここでは複素数の積分を行っている。
ところで、ガウス関数が確率密度関数のときの特性関数はやはりガウス関数である（ガウス関数のフーリエ変換はやはりガウス関数である）。ガウス確率密度関数の特性関数は
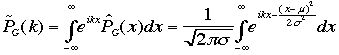より計算される。指数関数の肩はつぎのようにかかれる。
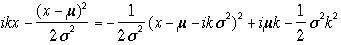変数変換：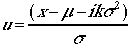
をおこなうと、
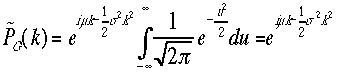というガウス型をしていることがわかる。従ってx=x1+x2においても x1,x2の特性関数がガウス関数に従い、両者の和x1+x2は特性関数同士の積となり二つのガウス関数の積となる。
、
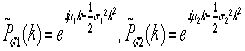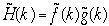より、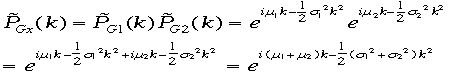
となり<x>=<x1>+<x2>,
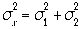とともに、ガウス関数となることが示される。