物理 実験学　　(6)

竹下徹　(029july2004)

推定： 実験結果から本当の値を推定するにはどうするか？
種々の測定があるとき、結果はその関数であるときどうやって推定するか。
真の値がaのときある測定値ｘを得る確率密度をとする、一連の複数の測定結 果{x1,x2,x3,,,xN}の結果を得る全体の確率密度=と 各測定の確率の積でかかれる。ということは測定値xiの関数f(x1,x2,,, xN)があるとき、その平均値<f(x1,x2,,,xN)> は確率解釈をすると、一変数にまねて

を

と して、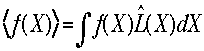と 書いてしまおう。このとき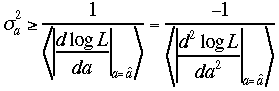が 成立する。この式は MinimumVariance Bound (MVB)と呼ばれる式が証明されている。ここでは真 の値の 推定値を意味する。我々が計算できるのはこのの 値のみであ る。
例えば分布がガウス分布に従うとき、
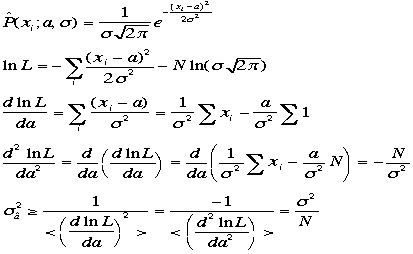な ので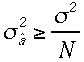が 成立する。ここではつまりすべての精度が等しいときには、大数の法則が成 り立つなら、推定値と真値は等しい。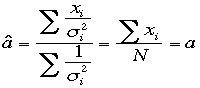N 個の同種の測定から得られ る分散と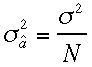の 関係が成立する。つまり中心極限定理でしめし た複数のガウ ス分布をする測定の分散は1/Nになる結果と一致する。

推定法：Maximum Likelihood (ML) 推定法（最ゆう（尤）法）：Lの最 大値を与えるaの推定値を 与えるという方法で各xiがガウス分布するとき（確率密度関数として　ガウス関数を取って）、（た だし全ての分散は等しいとする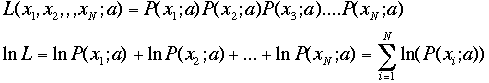）がL の定義で、すべてPの積の形なのでlnLはlnP の和となる。これをガウス分布の場合に 当てはめると、すべてのi について和を取ると、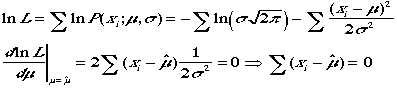という当たり前の答えを得る。これは、正しい 推定では 推定された平均値とデータの平均は一致するというものだ。一方分散の推定では、と なる。

問題：ポアソン分布に対するML推定を行え。

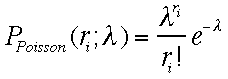各riがポアソン分布する（つまり、離散型の時は正確に確率Pの積としてLを定義できる）とき、がL の定義で、すべてPの積の形なのでlnLはlnP の和となる。これをポアソン分布分布の場合に当てはめると、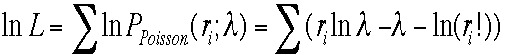こ れは、正しい推定では推定された平均値に対 して次の式がなりたつ。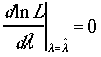。実際のポアソン　分布の関数形を代入する と、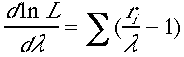と なり、で これがゼロとなるから

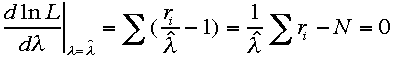より、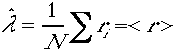 をえる。つまりポアソン分布するデータriの平均値がポアソン分布の期待値λの推定値を与えている。
問題：指数分布に対するML推定を行え。￥グラフは　上に凸になる。頂点が最大値で=

推定法：Maximum Likelihood 推定法の応用

データの組(xi,yi)が得られるとき、例えば、ストップウオッチで移動する物体の速さを測ろうとするとき、xiは道につけられた位 置を表し、 yiは時計の読みである、このときaは速さと言う関係になる。

測定データからある量aを推定する方法のうちyiがf(xi,a)との差がガウス分布をとるとき最小二乗法と呼ばれる。こ のlnL<0は負であり、複数のデータ （xi,yi）の組からaを推定することは、lnLの最大値(Maximum Likelihood)（Lは確率あるいは（離散型の場合）、確率密度関数の積　であるのでほぼ最大確率を意味する）を与えるaを求めることである。
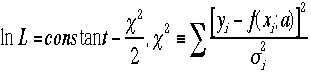と いうことは この定義によるカイ二乗の最小値を求める
事に相当する。そのため、これを最小二乗法と呼ぶ。lnL の最大値を探す　Maximum Likelihood法はMVBにより最小の分散を探 すことに相当する。なぜ なら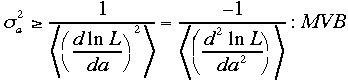で あるから。推定法：最小二乗法
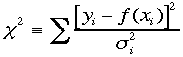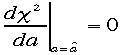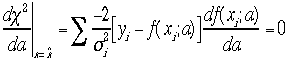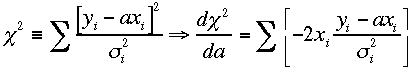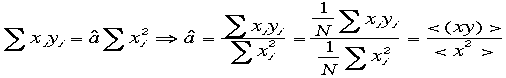
データの組(xi,yi)が得られるとき、yiがf(xi,a)との差がガウス分布をするとき最小二乗法と呼ばれる。こ の定義によるカイ二乗の最小値を求めるには、を満たすを 探し当てればよい。つまり次の式を計算する。次はf(xi,;a)の形を決めないと計算不可能なの で、まず、の時を考える。計 算を簡単にするためにすべての*が等しい場合を考え よう。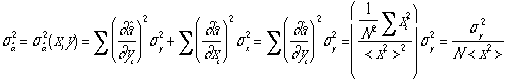こ こでは　x方向の精度は無限に良い、すなわち＝０としてy方向の精度のみ問題にした。

問題：等速直線運動を観測し、次の時刻tと位置xのデータを得た。
t 0 1.0 2.0 　 3.0 　 4.0 　 5.0 (秒）
x 0 14.5　30.3　　43.8　　58.9　　77.1　（ｍ）　速さ、と速さの精度とカイ二乗を計算せよ。B　時間の精度は大変良く、一方位置の測定 精度がそれぞれ+-0.5mとする。

最もよく使われるのはこの式のもうちょっと一般化された一次式である、なぜなら　y=f(x)=axというのはx=0でy=0を要求し ており、強い 制限を課しているからである。それに対してここで行うy=f(x)=ax+bの場合それがない線形で一般的な場合である。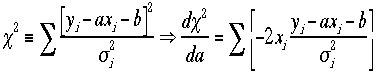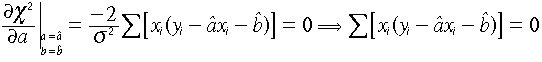つ まりを 得る。同様にbについて微分して0であるこ とを要求する と、
a,bについての連立方程式と見立てて、解くと。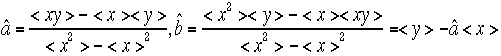を 得ることになる。こうして原点が不確かな実験にあってもこれもfittingの自 由度として取り入れて決定できる。さて次はこれの精度を表す量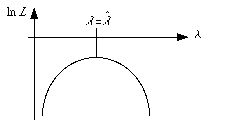を 計算しよう。精度の伝搬式より、ま た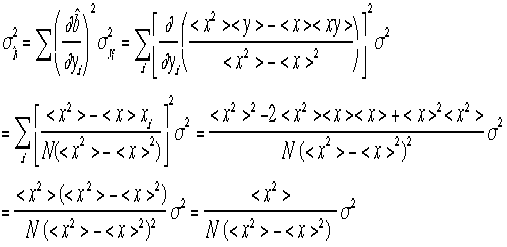と 計算できる。今まではずうと計算の楽さの ために等しいの場合を計算して来たが、異なる場合は、と いう置き換を行い、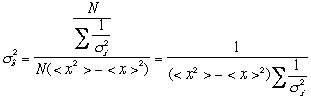とすればよい。

このさてこのカイ二乗は分布関数の一つである。すなわちガウス分布や指数分布のようにである。カイ二乗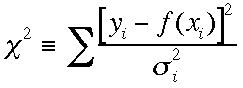は[(y の測定値)-(yの理想値)]の二乗/(yの精度の二乗)と読め る。カイ 二乗が小さいということは測定値が理想値に近い事を表している。逆にカイ二乗が大きいということはy=f(x)という関数への当てはめがよろしくない、あ るいは間違っている事を示唆している。カイ二乗をyと関数への当てはめの良さを表す量として定義した。これを確率で表して、分布関数とする。そのためには f(x)に含まれる変数(f(x)=ax+bの時はaとbの二つが変数の数nvとして、測定点数をNmとし、Nm-nv=nを自由度という。この自由度n の時のカイ二乗がいくらになる確率がカイ二乗分布と呼ばれる。次の式でかかれる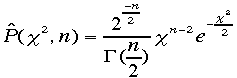：こ こでは ガンマ関数である。
グラフの形は、図のようであり、の極 限でガウス関数に近づく。但しそ の平均値は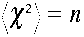を満たす。ここでnは自由度である。この式 はつまりカイ 二乗の平均値は自由度程度になるべしと主張しているわけだ。従って測定点が５個あってfittingに２個の変数を使ったときは、自由度nはn=5-2= 3であり、カイ二乗を計算して３より大変小さい（たとえば０．１）とかるいは１０とかいう値を取った場合は、fitting関数f(x)が不適切と見なす べきである。あるいは定義から明らかなようにガウス分布する測定量の二乗の和は自由度nのカイ二乗分布をする。ちなみにガウス分布する測定量の和の分布は ガウス分布である。

下の図で横軸はカイ二乗で、縦軸は確率密度関数値である。
線は各n=1(d),2(e),3(f),5(g),10(h)に対応している。

確率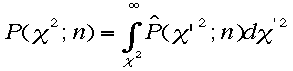はこの式で与えられる。が 横軸なので、これで積分する必要がある。の値が実験結果として得られたとき、その値の平均値はn(自由度) に一致するた め、 これから遠く離れる確率は小さい。これを表すのが以下のの表 である。

n（自由度）	確率=10%	5%	2%	1%
1	2.71	3.84	5.41	6.63
2	4.61	5.99	7.82	9.21
3	6.25	7.82	9.84	11.34
4	7.78	9.49	11.67	13.28
5	9.24	11.07	15.03	16.81
6	10.64	12.59	15.03	16.81
7	12.02	14.07	16.62	18.47
8	13.36	15.51	18.17	20.09
9	14.68	16.92	19.68	21.67
10	15.99	18.31	21.16	23.21
11	17.27	19.68	22.62	24.72
12	18.55	21.03	24.05	26.22
13	19.81	22.36	25.47	27.69
14	21.06	23.68	26.87	29.14
15	22.31	25.00	28.26	30.58
20	28.41	31.41	35.02	37.57
25	34.38	37.65	41.57	44.31
30	40.26	43.77	47.96	50.89

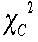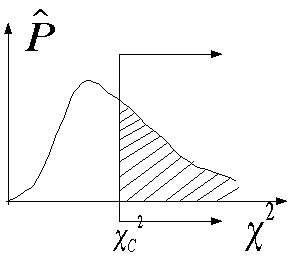
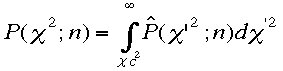表の横軸10%,5%,2%,1% はそれぞれ積分された確率であり表はその確率を与える区切りとなる を あたえている。グラフでしめすと、を 満たす。例えば測定点が17点あり、fittingを直線で行うと(f(x)=ax+b)２個の自由度がここで失われ、n=17-2=15となる。このと きが22 であったとするなら、この結果は10％以 上の確率で起 こり、充分に良い結果として指示される。もしが 30となると、これが起こる確率は1％程度であり、とてもまともな結果とは考えられないという尺度をあたえる。このとき、１次関数をやめて２次関数で fitして、が24程度になった場合、自由度は14で、その 確率は5％出 有り、改善が認められ、１次関数より２次関数が好まれる。一方余りが小 さい場合も危険である。本来確率密度関数のピークは<> =nにありここから離れる事は起こりにくい。この場合、精度因子が大 きすぎる場合がある。もちろんあまりデータと理論線が近い場合はその他の理由が有るかもしれない、これを疑うべきである。

MinimumVariance Bound (MVB)と呼ばれる式の証明。
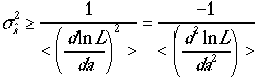
推 定のよりどころが、この式である。
よって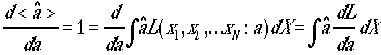一 般にな ので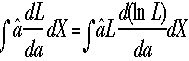ま た確率の定義より、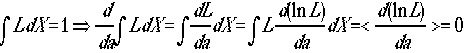よってと いう関係式が得られる。
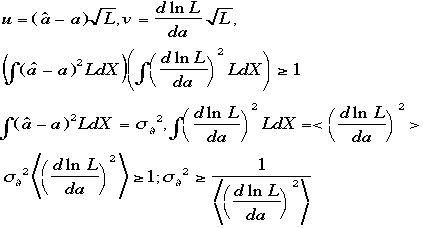Schwarzの式：　があるので、（例えばよっ て式 は成立つ。この式はをしめす。

2番目の等号の証明