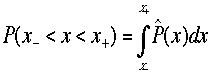 これは両側で取った場合である。片側の場合は、
これは両側で取った場合である。片側の場合は、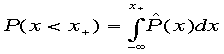 のとき、上限が信頼度
のとき、上限が信頼度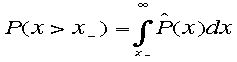 のときは、下限が信頼度
のときは、下限が信頼度物理実験学 (7)
竹下徹 (03july2002)
信頼度:
ガウス分布する量xが有り、平均値を<x>、標準偏差をs とするとき、 この分布から一つ取り出しその値yが [<x>-s]≦y≦[<x>+s]
の間に入る確率は68%である。これを信頼度68%であると言う。同様にガウス分布する場合95%の信頼度の区間は、[<x>-2s]≦y≦[<x>+2s]
である。また[<x>-2.58s]≦y≦[<x>+2.58s] を満たすときは99%信頼度である。式で表すと、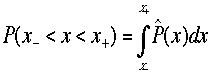 これは両側で取った場合である。片側の場合は、
これは両側で取った場合である。片側の場合は、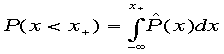 のとき、上限が信頼度
のとき、上限が信頼度![]() で存在し、
で存在し、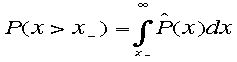 のときは、下限が信頼度
のときは、下限が信頼度![]() で存在する。ガウス分布を仮定し片側ののみ考えるとき、84%信頼度でx<x+sである。また信頼度90%である区間は x<1.29sである。
で存在する。ガウス分布を仮定し片側ののみ考えるとき、84%信頼度でx<x+sである。また信頼度90%である区間は x<1.29sである。
仮説と検定:
我々は実験を行いその結果がある理論で説明できるかどうかに興味がある。またその理論に含まれるパラメータの値を実験により決定する事が目的であることが多い。しかしパラメータは通常実数値であり、「値はいくらである」という結果はあり得ない。実数だから、いくらからいくらの間にある(実は、いくらの確率で)としか我々は結論できない。そう普通我々はこれこれの実験を行い、なになにを測定し、 x +- dx である、と結論するときは、 測定値はxであったとしても、 通常 x-dx < x < x +dx に入る確率は68%であると結論しているのだ。
仮説は、例えば 仮説 H0 「この測定値 x +- dx が予言される値 A と等しい」 という風にたてる。そしてこれをテスト(検定)する、つまり実験により測定される未知のパラメータの値について「この測定値が予言される値と等しい」という仮説が棄却されるかどうかをみる。これを仮説検定あるいは検定(test)という。もしこの仮説が正しいなら x はガウス分布すると仮定すると、 信頼区間を99%に設定すれば、Aが [x-2.58dx]≦A≦[x+2.58dx]
を満たせば、 仮説が成り立つと考えられるし、反対に 成り立たない場合つまり [x-2.58dx]>A かあるいはA>[x+2.58dx]のときは、仮説 「この測定値
x +- dx が予言される値 A と等しい」 は棄却される。この論理が実際仮説検定でどのように使われるかを分散![]() の値が判っているガウス分布において平均値
の値が判っているガウス分布において平均値![]() について仮説検定について説明する。これは単なる長さの測定といった測定が想定され、測定は複数の測定データからなる、これをxiとするi=1,2,3,...n。仮説H0:
について仮説検定について説明する。これは単なる長さの測定といった測定が想定され、測定は複数の測定データからなる、これをxiとするi=1,2,3,...n。仮説H0: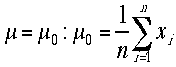 の検定を考える。
の検定を考える。![]() が未知の値であり仮説は
が未知の値であり仮説は![]() である。H0が真であるときデータの平均
である。H0が真であるときデータの平均![]() はガウス分布(平均値
はガウス分布(平均値![]() ,分散
,分散![]() )に従うはずである。理論的結論は分布であり、実験が得る結論は値 たとえば
)に従うはずである。理論的結論は分布であり、実験が得る結論は値 たとえば![]() である。つまり分布と1点の値を比較することになる。その比較は実際に得られた(統計)量が分布図においておきやすい値であるのか、おきにくい値であるのかを見ることになる。もしおきにくい値であるなら理論分布と実験結果は食い違っていると判断し、H0を棄却する。具体的には小さな確率αを設定し、この領域を棄却域と呼ぶ。H0が真であるなら実験値がこの棄却域に落ちる確率はたかだかαであり、この領域に落ちることはほとんど無いと言うことを表している。従って現実に得られる値を計算し実験値が棄却域の中におちれば 仮説 H0を棄却する。反対に現実に得られた値つまり実験値が棄却域の外におちれば 仮説 H0を棄却しない、という判定をおこなう。この判定にもちいられる小さい確率αは有意水準または危険率と呼ばれる。通常 0.05 あるいは0.01が使われる。こうして得られる検定を有意水準αの検定という。有意水準α=0.05でガウス分布が対象の場合棄却域を両側に設けるとすると
である。つまり分布と1点の値を比較することになる。その比較は実際に得られた(統計)量が分布図においておきやすい値であるのか、おきにくい値であるのかを見ることになる。もしおきにくい値であるなら理論分布と実験結果は食い違っていると判断し、H0を棄却する。具体的には小さな確率αを設定し、この領域を棄却域と呼ぶ。H0が真であるなら実験値がこの棄却域に落ちる確率はたかだかαであり、この領域に落ちることはほとんど無いと言うことを表している。従って現実に得られる値を計算し実験値が棄却域の中におちれば 仮説 H0を棄却する。反対に現実に得られた値つまり実験値が棄却域の外におちれば 仮説 H0を棄却しない、という判定をおこなう。この判定にもちいられる小さい確率αは有意水準または危険率と呼ばれる。通常 0.05 あるいは0.01が使われる。こうして得られる検定を有意水準αの検定という。有意水準α=0.05でガウス分布が対象の場合棄却域を両側に設けるとすると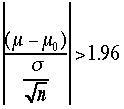 のときH0を棄却する。反対に
のときH0を棄却する。反対に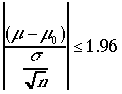 のときH0を棄却しない。この仮説検定において「仮説を棄却しない」ということを仮説が正しいと主張するものでは有りませんので、混同しないでください。あくまでこの意味は仮説を棄却する根拠は十分ではないというだけです。一般に仮説が正しい事を示すにはさまざまな角度からの検討が必要であり、まず不可能に近い。これに対して、仮説が疑わしいことはデータをもちいて示すことが比較的容易である。ですから仮説検定にもちいる仮説としては、疑わしいと思うことを仮説として採用し検定を行うべきである。この意味において検定しようとする仮説を帰無仮説という。また有意水準αを小さな値に取ることもこの帰無仮説を取ることによる。仮説検定において仮説H0が有意水準αの検定で棄却されるとき、、仮説H0は有意水準αで有意であるという。また棄却されるときは、仮説H0は有意水準αで有意でないという。
のときH0を棄却しない。この仮説検定において「仮説を棄却しない」ということを仮説が正しいと主張するものでは有りませんので、混同しないでください。あくまでこの意味は仮説を棄却する根拠は十分ではないというだけです。一般に仮説が正しい事を示すにはさまざまな角度からの検討が必要であり、まず不可能に近い。これに対して、仮説が疑わしいことはデータをもちいて示すことが比較的容易である。ですから仮説検定にもちいる仮説としては、疑わしいと思うことを仮説として採用し検定を行うべきである。この意味において検定しようとする仮説を帰無仮説という。また有意水準αを小さな値に取ることもこの帰無仮説を取ることによる。仮説検定において仮説H0が有意水準αの検定で棄却されるとき、、仮説H0は有意水準αで有意であるという。また棄却されるときは、仮説H0は有意水準αで有意でないという。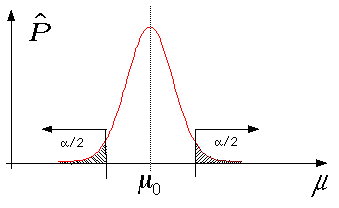
逆に上の図の内側に入る場合は有る信頼度で区間推定を行うことができる。それは、例えばガウス分布に従うデータがあり、その分散![]() が判っているときに平均値を推定する場合を考えよう。n個のデータ xi
から平均 <x>を得ることができる。さて測定値から得れられるガウス分布の中心値の推定はもちろん
が判っているときに平均値を推定する場合を考えよう。n個のデータ xi
から平均 <x>を得ることができる。さて測定値から得れられるガウス分布の中心値の推定はもちろん![]() である。さらにその推定値の精度を求めよう。推定値
である。さらにその推定値の精度を求めよう。推定値![]() は中心値<x>, 分散
は中心値<x>, 分散![]() でガウス分布するので、推定値
でガウス分布するので、推定値![]() は確率68%で区間 [ <x> -
は確率68%で区間 [ <x> - ![]() ]
<
]
< ![]() < [ <x>
+
< [ <x>
+![]() ] にある。また確率95%で [
<x> - 2
] にある。また確率95%で [
<x> - 2![]() ] <
] <
![]() < [ <x>
+2
< [ <x>
+2![]() ] にある。この確率のことを信頼度(=1-α)とよぶ。またこの区間を信頼区間という。式で表すと、
] にある。この確率のことを信頼度(=1-α)とよぶ。またこの区間を信頼区間という。式で表すと、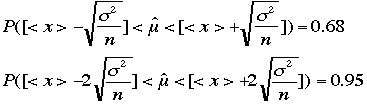 とかける。
とかける。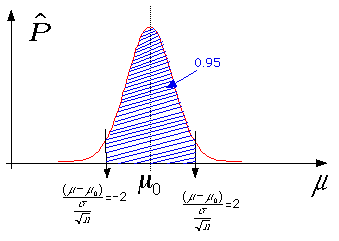
さてカイ2乗分布はガウス分布する量の2乗和(たとえば精度は2乗で伝搬する)の分布であることは述べた。この分布に従う量に関して検定を行うことがある。例えばガウス分布するデータ x1,x2,x3,,,,xnからこのデータを取り出す元の分布(母集団という)の分散を推測するときである。仮説H0は母集団の分散
![]() =
=![]() (ある定まった値)であり、データから得られる2乗和をSとして、
(ある定まった値)であり、データから得られる2乗和をSとして、
![]() 、
、![]() は自由度(n-1)のカイ2乗分布に従うことが知られている。従って
は自由度(n-1)のカイ2乗分布に従うことが知られている。従って![]() を適当に棄却域を設定して検定すればよい。例えば仮説H1:
を適当に棄却域を設定して検定すればよい。例えば仮説H1:![]() >
>![]() をたててH0が間違っていることを考察するばあい、
をたててH0が間違っていることを考察するばあい、![]() は大きな値を取ることが予想される。従ってH1が正しいときは棄却域を全部右に持って来る。よって検定は
は大きな値を取ることが予想される。従ってH1が正しいときは棄却域を全部右に持って来る。よって検定は
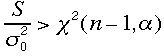 とする。これは次の図に対応する。
とする。これは次の図に対応する。
この反対に![]() の信頼区間を求めるには
の信頼区間を求めるには![]() が自由度(n-1)のカイ2乗分布に従う事をもちいて
が自由度(n-1)のカイ2乗分布に従う事をもちいて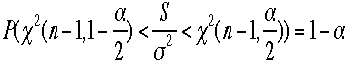 が得られる。式を変形すると、
が得られる。式を変形すると、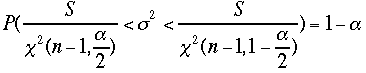 より
より![]() の信頼度1-αの信頼区間は
の信頼度1-αの信頼区間は![]() から
から![]() までとなる。
までとなる。