演習問題:
摩擦のない斜面(長さL、角度 )上で物体を滑らせてその時間(t)を測定した。
)上で物体を滑らせてその時間(t)を測定した。
ここで実験に使った測定量は、斜面の長さ(L)と角度(theta)と時間(t)であり、それぞれの測定精度をsL,sthera,stとする。関係式は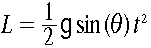 である。
である。
重力加速度gとその精度を求めよ。
L=1.0(m),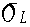 =0.01(m),
=0.01(m), =30.0(度)、
=30.0(度)、 =1.0
(度)、t=0.65(s),
=1.0
(度)、t=0.65(s),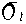 =0.05(s)とする。
=0.05(s)とする。
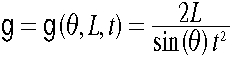 であ
るので、gを各変数の関数として偏微分する。
であ
るので、gを各変数の関数として偏微分する。



目標であるgの精度を表す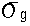 は精度の伝搬式で表される。
は精度の伝搬式で表される。
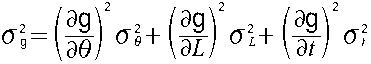
まず、重力定数gは3つの量(L,theta,g)の最適値つまり平均値を代入して次ぎように答える。
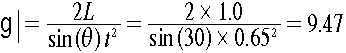
有効数字を考慮すると、2桁に丸めるべきである。従ってg=9.5.
ここまででは中学生(小柴先生談)
精度の伝搬式の各項は次のようににかける。

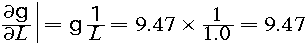

これらを精度の伝搬式に代入して、
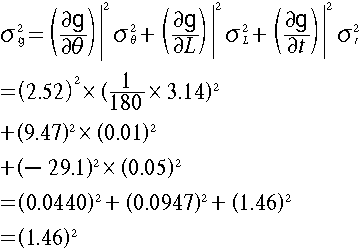
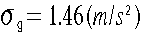
有効数字を考慮すると、gの有効は小数点下1桁までなので、

よって答えるべき値は、
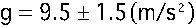 と
なる。
と
なる。
この値をよく見て考えてほしい。なんでこんなに精度を表す数値が大きいのか。
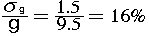 の
相対精度である。
の
相対精度である。
おのおのの精度は、長さが ,
,
角度が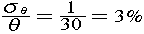 ,
,
時間が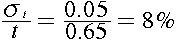 である。
である。
一番相対測定精度が悪いのは時間であり8%である。精度の伝搬式によれば
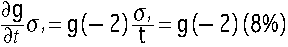 であり、これがきいいている!一番支配的な効果を表している。各項は2乗の
和の形をしているので、大きいものが一番効く!
であり、これがきいいている!一番支配的な効果を表している。各項は2乗の
和の形をしているので、大きいものが一番効く!
その結果2*8%=16%の相対精度を生み出している、という事だ。実験を行うとき、
この依存性に注意い払うべきであることが分かる例である。
 )上で物体を滑らせてその時間(t)を測定した。
)上で物体を滑らせてその時間(t)を測定した。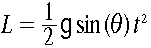 である。
である。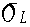 =0.01(m),
=0.01(m), =30.0(度)、
=30.0(度)、 =1.0
(度)、t=0.65(s),
=1.0
(度)、t=0.65(s),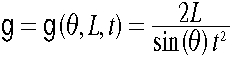 であ
るので、gを各変数の関数として偏微分する。
であ
るので、gを各変数の関数として偏微分する。


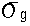 は精度の伝搬式で表される。
は精度の伝搬式で表される。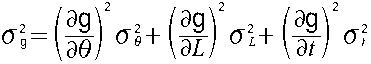
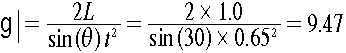

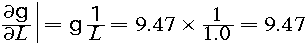

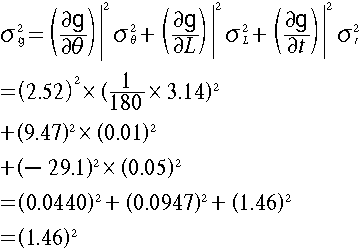
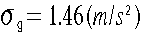

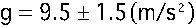 と
なる。
と
なる。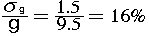 の
相対精度である。
の
相対精度である。 ,
,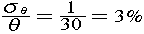 ,
,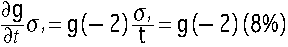 であり、これがきいいている!一番支配的な効果を表している。各項は2乗の
和の形をしているので、大きいものが一番効く!
であり、これがきいいている!一番支配的な効果を表している。各項は2乗の
和の形をしているので、大きいものが一番効く!