1998年度修士論文
追従Modelにおける
一次元交通流の研究
信州大学大学院理学研究科数学専攻
佐野 淳次
近年車が増加し、交通流において渋滞は避けられないものになってきた。交通流を研究するためのいくつかの研究法がある。交通流は主に3つの考えがある。それは、交通流を連続なものとして扱うマクロなアプローチ、交通流を構成している車1台1台を個別に扱うミクロなアプローチ、それと確率論的な手法を用いたアプローチである。交通運動のもっとも強い印象を与えるものの一つは交通渋滞である。渋滞の中でも交通事故や信号機のように特別な原因で生じたのではなく、小さな乱れによって生じる渋滞が存在すると考える。Simulationは4次のルンゲクッタ法を使い、車の長さは無視し、周期境界条件を使っている。ミクロなアプローチにおいて主流なものの1つである追従Modelを考え、その中でも、古典的な追従Model、板東らの最適速度Model(OV
Model)、早川・中西の最適速度Model(ここではUV Modelという)を中心に議論し、simulationを行い、渋滞現象を詳しく調べる。古典的な追従Modelは運動方程式として1階の微分方程式であり、ドライバーの時間的遅れを考慮するために差分方程式となっている。板東らの最適Modelは![]() =
=![]() 、
、![]() という2階微分の方程式を考えている。aはドライバーの感度であり、
という2階微分の方程式を考えている。aはドライバーの感度であり、![]() はn番目の車の位置で、・は微分を意味する。ここで、
はn番目の車の位置で、・は微分を意味する。ここで、![]() という関数をあてはめている。U(h)は単調増加関数で、U(0)→0でU(L)→一定である(Lは道路全長)。この運動方程式は定常解が存在し、揺らぎを加えて安定条件を求めると、
という関数をあてはめている。U(h)は単調増加関数で、U(0)→0でU(L)→一定である(Lは道路全長)。この運動方程式は定常解が存在し、揺らぎを加えて安定条件を求めると、
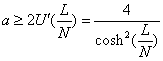 となる。OV
Modelでのsimulationの結果、渋滞現象が現れて、渋滞領域と非渋滞領域の範囲が安定性に関する解析理論と一致した。次にバックミラーの効果を入れた早川・中西のModelを考える。早川・中西の最適速度Modelは
となる。OV
Modelでのsimulationの結果、渋滞現象が現れて、渋滞領域と非渋滞領域の範囲が安定性に関する解析理論と一致した。次にバックミラーの効果を入れた早川・中西のModelを考える。早川・中西の最適速度Modelは
目次
1. 序章
プログラム
謝辞
参考文献
1
序論近年、車が増え交通手段の一つとして重要な役割を果たしている。人や荷物を手軽にいろいろな場所へ運ぶことができる。しかし、これだけ車が氾濫すると交通問題も交通渋滞、交通事故、交通規則違反など様々な問題が生じて、交通流を妨げている。
交通運動のもっとも強い印象を与えるものの一つは交通渋滞である。渋滞がどのように運動展開しているのかについて興味がある。交通渋滞の中には交通事故や信号機のような特別な原因ではなく、小さな乱れによって生じる渋滞が存在すると考える。この種の渋滞は高速道路でしばしば観察される。高速道路で何台かの車が等間隔で走ることが難しいことは経験的に分かっている。ちょっとしたブレーキなどが小さな乱れとなる。ここで、そのような渋滞に注目し、渋滞と非渋滞との間での相転移に興味を持ち、その構造の特徴を研究していく。交通流を研究するためのいくつかの研究法が存在する。交通流は主に3つの考えがある。それは、交通流を連続なものとして扱うマクロなアプローチ、交通流を構成している車1台1台を個別に扱うミクロなアプローチ、それと確率論的な手法を用いたアプローチである。交通流に対する理論的取り扱いの一つにマクロな立場から交通流をとらえる流体力学的なものがある。流体力学的な交通流のModelは、一般的に基本図というマクロで定常な量からダイナミックな記述を行うというModelである。このとき観測されているマクロな基本図から平均速度が密度によってどのように表されるかという関数形を仮定して解析される。従ってマクロな流体力学的Modelは実際に観測されている基本図を用いた現象論であるということができる。この現象論でもいろいろな交通流の現象を研究することができるが、実際の交通流を基本図も含めて再現するようなModelを研究する事は適当である。実際の交通流を基本図も含めて再現する事を目的とするとき、Model化には車を個別に取り扱いその間の相互作用を考えることから始める。よって、ミクロなアプローチにおいて主流な追従Modelを考える。この論文において、古典的な追従Model、板東らの最適速度Model(OV Model)、早川・中西の最適速度Model(ここではUV Modelという)を中心に議論していく。
1.2 実際の交通流[1]
交通流の現象でよく用いられる言葉を整理する。交通流全体の状態を表すのに用いられる最も基本的な量は3つあり、それぞれ交通量、密度、平均速度である。交通量はある時間内に道路の観測点を通過する車の数で定義される。すなわち、ある観測点でT時間に通過する車の数を計測した結果をm台とすれば、T時間交通量Qは、
![]() (1.1)
(1.1)
と書ける。この交通量とよく似ているが区別される量に交通流率がある。交通流率とは、単位時間あたりに換算された交通量のことである。従って、交通流率qは交通流で観測した交通量の結果から
![]() (1.2)
(1.2)
次に基本的な量は密度である。これは道路上の単位距離あたりの車の数で定義される。交通流率と密度の関係を表した図を基本図と呼ぶ。ここでは実際に観測されている交通流の性質を紹介する。この基本図という量は実際観測されるときは、ある道路上の一点である日時にある時間観測される。そのためデータには場所による違いや測定日時による違い、測定時間による違いなどの多くのばらつきがある。越らによる実際の交通流率と密度の関係の典型的な観測結果を図(1.1)に示す。[2]このデータは1号線上り方面浜崎橋合流部の上流約5.7kmでの1分間ごとのデータを一時間あたりに換算したplotである。2つあるのは走行車線(outer lane)と追い越し車線(inner lane)のデータである。このように同じ道路のデータであっても車線によって基本図は大きく変わる。このデータから分かるのが低密度では交通流率がほぼ時速45kmの直線に平行であり、高密度では何か別の曲線にのって小さくなっていく様子が見られる。また、高密ではデータのばらつきが大きく低密度ではばらつきが小さいことが見て取れる。この図から低密度と高密度では明らかに交通流の特性が違うことが分かる。最も特徴的なのが低密度から高密度に移り変わるところである。このような交通流率が低密度と高密度では特性が違うということは以前から知られていた。この違いを初めて指摘したのはEdieである。[3]EdieはGreenbergの交通流に対する流体力学的なModelで得られていた密度と交通流率の関係の解析的な式を用いて、観測されたデータのフィッティングを行った。この結果、低密度と高密度では別々のパラメーターを用いてフィッティングする必要があることを指摘し、基本図で交通流率が不連続になることを示した。またこれ以降の研究もModelこそ違うがやっていることは密度領域を2つに分け別々にフィッティングするということである。このように2つの領域に分けるという考え方では基本図を何か不連続な関数で記述する事になる。これはある密度で突然移り変わると解釈されているものもあれば、ある密度幅があり、徐々に移り変わると解釈されているものもある。ここで示した越らの観測データはある密度を境にして、突然別の曲線にのるというような不連続な振る舞いではなく、むしろある密度の幅があってその間で徐々に移り変わっている振る舞い(走行車線)や、全く違う密度-交通流率の関数が、ある密度領域で共存して双安定な構造をつくる移り変わっているような振る舞い(追い越し車線)をしている。越らはこの結果から交通流率はギリシャ文字λを鏡に映したような形の不連続性を示すといっている。Hallらはこのような観測で得られている低密度と高密度での交通流率の特性の違いを調べるために、オンタリオの高速道路での長期のデータを用いて解析を行った。[1][4]このときにHallらは、今まで用いられてきた方法とは違う解析方法を用いた。今まで使われていた解析方法は交通流のModelの計算からの関数形の仮定や、密度領域の分割にどうしても解析する側の意志が入ってしまうためである。Hallらはこのような不確定性をなくすために、ただ一つの「交通流率は密度(occupancy)が決まれば一意に決まる。」という仮定をおいて一つの密度に対して得られている交通流率の平均を取るという解析を行った。この結果、図(1.2)のようなバラバラとした点で表現された基本図[5]が図(1.3)のような平均を取った基本図になる。[5]図(1.3) では、平均を取った交通流率に直線的である自由流とガタガタとしている渋滞流の区別がはっきりと見えている。またデータの標準偏差(図中では実線で書かれている。)は自由流よりは渋滞流の方が大きい。そして、最も標準偏差が大きくなっているのはちょうど臨界的な占有率のあたりである。この解析の結果、交通流率はVの字の上下を入れ替えたような形をしており、低密度から高密度の自由流から渋滞流に移り変わるところは連続であるが微分はできないような関数で表されているとHallは主張している。また、図(1.2)を見れば分かるように臨界的な占有率のところでのデータがあまりない。このため観測時間が短かったりすると、このあたりのデータを十分に取ることができなくなる。Hallらはこの問題にもCatastroph Theory Model[6]という回答を下している。Catastroph理論を交通に応用したのはHallが始めてではなく、それ以前にDendrinosが1978年に[7]、Navinが1986年に[8]それぞれCatastroph理論を交通流に応用している。HallのCatastroph Theory Modelの本質は、交通流の特性を表す密度-交通流率の関係をCatastroph理論のなかでもcusp Catastrophを用いて理解しようというものである。cusp Catastrophは状態を表す変数xと二つのコントロールパラメターu,vで表され、xは時間に対し離散的であり、u,vは時間に対して連続な振る舞いをするような量である。このcusp Catastrophを示すような形はポテンシャルV(x)
V(x)=x4+ux2+vx (1.3)
を最小にする状態で記述される。すなわちこのポテンシャルの平行曲面dV/dx=0上に変数の値をとる。この平行曲面がx、u,vで張られる三次元空間に埋め込まれたcusp Catastroph多様体
4x3+2ux+v=0 (1.4)
を定義する。この多様体を決める三次方程式が一つの実根をもつためには三次方程式の判別式
D=8u3+27v2 (1.5)
が正でなければならないことはすぐに分かる。Hallらはこの状態を表す変数xとして平均速度をとり、二つのコントロールパラメーターとして交通流率をu,占有率をvととった。この三つの量が多様体上にあると仮定すれば、このときの平均速度がコントロールパラメーターに対し一意に決まるためには、コントロールパラメーターの空間にとり得ない領域ができ、それが基本図での連続ではあるが微分不可能な関数という振る舞いにつながるとしている(図(1.4)[9])。また、観測されたデータを実際にplotしたのが図(1.5)である。[9]これは交通流率と占有率、平均速度の三次元plotでありオンタリオの高速道路のデータである。またこのデータのそれぞれの平面への写像がどのようになるか示したのが図(1.6)である。[6]これは図(1.5) の直接の射影ではないが外形は同じである。
次に交通流の時空間の軌跡の観測を紹介する。このような観測は渋滞流で発生する粗密波の伝播を調べたり、直接渋滞相の発生を調べたりするのにも用いられる。このような時空間の車の軌跡の観測例を一つ紹介する。図(1.7)はアメリカの高速道路で空中から撮られたものである。[10]この図で横軸が時間、縦軸が空間である。黒い線の一本一本が車一台一台の軌跡を表す。この図では車の粗密波の一つの密の波が発生し、それが車の進行方向とは逆に進んでいく様子が観測されている。このような粗密波が車の進行方向とは逆に進む現象は一般的なものであり、この観測結果だけのものではないし、実生活の中でドライバーが日常経験するところである。また、この粗密波の中でも車の速度がいろいろあることが見てとれ、粗密波が発生して消えるまでの間に車が動いているものや止まっているものがあるのが分かる。また粗密波の内部に車が入る前には、ある速度で走っていた車がその速度を落としている領域が見られ、その領域を抜けた後で粗密波の更に速度が遅い領域に入っているという二段階の減速過程が見られる。粗密波から抜け出てるところではこのような段階を踏んだ加速は見られずいきなり車が抜け出しているのが分かる。
また、車を運転するとき、前の車の位置によってどのような振る舞いをするかという追従挙動が越らによって調べられている。追従挙動はミクロな車の運動を直接表し、このミクロな追従挙動がマクロな現象に大きく影響する。このような追従挙動は注目している車の車間距離とその速度で張られる空間上の一点で表すことができる。このような相空間における追従挙動の実験dataを図(1.8)に示した。[2]これは越らが行った追従挙動を調べる実験の結果である。[4]この図では加速したときの車の相空間での位置をA,減速したときの相空間での位置をDと書いている。この図では渋滞流と自由流の区別がはっきりとしており、ここでも渋滞流と自由流の交通流の特性の違いが現れている。また、図の中で減速Dは相空間の車間距離が小さいところに多く集まっており、加速Aは車間距離の大きいところに集まっている。これは加速時の方が減速する時よりも車間距離を多くとる傾向があることを示している。
2. 古典的な追従Model
ここでは、交通流のModelの1つである追従Modelを考える。追従Modelは典型的なミクロな立場からの交通流のModelであり、車を一台一台取り扱いその運動を連立微分方程式で取り扱うところに特徴がある。これは流体力学的な取り扱いをするマクロなModelではなく、車に働く力を考えてミクロなModel化を行い、実際の交通流を再現しようという目的で研究されている。各車の運動方程式は車の各ドライバーが他の車からの刺激に反応するという仮定をしている。車のドライバーが自分自身の感度を持って与えられた刺激に反応するという考えを導入するために、交通流において車の運動を左右する基本の方程式を導入しなければいけない。反応はドライバーに対して、直接の支配量のみである加速と減速により表現される。一般的に刺激や感度は車の位置の関数や導関数などである。この現象の背景の共通の普遍的な数学的構造が存在すると予想している。
2.1 Model
最も初期の頃の追従Modelに関する論文はPipesのものである。[11]Pipesは車の運動を現象的に考え、それが満たすべき方程式を導いた。まず一次元の追い越しがない状況で、車の理想的な車間距離を考える。今、k番目の車が速度![]() で走っているとする。理想的な車間距離はその速度で走っているときに、ある一定時間Tで車が進める距離と車が止まっているとき運転手が自然にとる車間距離bの和で表される。つまりk番目の車の位置を
で走っているとする。理想的な車間距離はその速度で走っているときに、ある一定時間Tで車が進める距離と車が止まっているとき運転手が自然にとる車間距離bの和で表される。つまりk番目の車の位置を![]() として、その前の車の位置を
として、その前の車の位置を![]() 、車の大きさを
、車の大きさを![]() とすると、前の車との車間距離は
とすると、前の車との車間距離は
![]() (2.1)
(2.1)
である。この時間微分をとれば、車の運動を記述する微分方程式が得られ、
![]() (2.2)
(2.2)
が車の運動を記述する方程式である。これは物理的な運動方程式
![]() (2.3)
(2.3)
と同値である。これを車の数だけ連立させて系全体の運動方程式が得られる。PipesはこのModelで一列に並んだ車が走り出したり、止まる様子を解析している。方程式(2.3)を調べよう。
![]()
![]() (2.4)
(2.4)
一番先頭の車の振幅f0を1とすると、k番目の車の振幅fkとその大きさは次のようになる。
![]() (2.5)
(2.5)
![]()
これからどの状態に対しても振幅は常に1以下になるので、系はどのようなときも安定に近づく。逆にそれぞれの車がとる戦略で感受率1/λをどんどん小さくすれば、不安定になることが可能である。しかし実際の交通流では、ドライバーは前の車の非常にわずかな速度の変化に直ちに反応し自分の車の速度を細かく調節するという運転はしない。このような非現実的な振る舞いに制限を付けるために、運転手の加速時の時間的な遅れを導入した次のような方程式をChandlerが導入した。[12]
![]() (2.7)
(2.7)
同じようにこのModelの安定性を考えるために
![]()
![]()
![]()
![]()
![]() (2.8)
(2.8)
である。これから![]() のとき安定であることが分かる。この安定になるための条件が感受率1/λに制限を与えModelの非現実的な振る舞いを押さえる。
のとき安定であることが分かる。この安定になるための条件が感受率1/λに制限を与えModelの非現実的な振る舞いを押さえる。
この2つのModelは、ともに速度の変化が相対速度にしかよらないModelであった。このために例えば車間距離が1km離れていても前の車が少し速度を変更すればその後ろの車が加速、減速をするというおかしな振る舞いをする。実際の交通流ではこんなことは起きない。このような点を改良したのがKometaniら[13]やGazisら[14]のModelであり、NewellのModelである。[15]KometaniらのModelはChandlerらの追従Modelに前の車の速度の項を付け足したようなModelである。GazisらのModelは現在でも観測データをフィッティングするのによく用いられている。また同時期にNewellも上記のようなおかしな振る舞いを改良したModelを提案している。GazisやNewellらのModelぐらいまでが古典的な追従Modelである。これ以降は追従Modelの基本的な精神はあまり変わっておらず、少しづつ状況に合わせた変更が行われている。運動方程式は主に2つの考えがある。1つ目は上記のように各車が2つの連続する車の速度関係に依存する。つまり、ドライバーの反応と関係速度の間に深く関係している。交通運動の初期の研究で、大部分のModelの運動方程式は基本的に時間に関して一階微分方程式を使う。交通運動のより簡単な研究の大部分はこの考え方に沿っている。しかし、この近似が現実的な理論となるためには、ドライバーの刺激に対する反応の時間的遅れに注意しなければいけない。それ故、方程式は差分方程式となる。もう1つは、各車の速度が2つの前後する車の距離関係に依存する。交通の一様状態流の不安定は解析的な方法で研究される。各システムにおいて最適速度がある。次の章で最適速度を考慮に入れるModelの一つであるOV Modelについて議論する。
3. OV Model
最適速度Model(Optimum Velocity Model:OV Model)の中でとりわけ簡単で解析が進んでいるのが、板東らによって発表されたModelである。[16]このModelにおいて、追従速度は、前の車との間隔に関する関数として導入される。板東らは交通流の安定性を分析し、交通渋滞の発展を時間発展により観察した。簡単のため、車の長さを無視し、すべてのドライバーが共通の感度を持っているという場合を考える。ドライバーは前方の車の運動に従いアクセルの踏み込みによる加速と、車間を安全に保持するための減速をしなければいけない。また、車の最高速度は法定速度であることを考慮に入れる。系の運動方程式は
![]() 、
、
![]()
ここで、Nは車の全体の数で、aはドライバーの感度(nに独立である)に対応する定数である。![]() はn番目の車の座標であり、・は時間微分を表す。異なる車は時刻tに同じ場所にはいない。
はn番目の車の座標であり、・は時間微分を表す。異なる車は時刻tに同じ場所にはいない。![]() は前方との車間距離
は前方との車間距離![]() で決まる関数であり、実際の交通流の観測から推定可能である。しかしながらその関数形の詳細は重要ではない。前の車が近づいてきたとき、ぶつからないために速度を十分に小さく下げなければいけない。他方、前方が空いていたら、車は速い速度で動くが、規制速度Umaxに制限される。よって、Uは次の特性を持つ関数である。
で決まる関数であり、実際の交通流の観測から推定可能である。しかしながらその関数形の詳細は重要ではない。前の車が近づいてきたとき、ぶつからないために速度を十分に小さく下げなければいけない。他方、前方が空いていたら、車は速い速度で動くが、規制速度Umaxに制限される。よって、Uは次の特性を持つ関数である。
更に、周期境界条件を設定する。つまり、車は長さLのサーキットの上を走り、(N+1)番目の車は、1番目の車に等しい。追従挙動が実際の交通流に対する観測や実験結果を元にして非線形な関数でModel化されている。このような非線形な関数を用いたModel化はGazisらやNewellによっても行われているがそれらは本質的に速度が車間距離や相対速度で決まるというModelでは一階の微分方程式で記述される。板東らが行ったのは、加速が車間距離と現在の速度の非線形な関数で記述されるというModel化で、これは時間に関する二階の微分方程式である。このために以前からModelに導入されていた加速に関する時間遅れの効果を手で入れなくてもよいと板東らは主張している。
板東らはこのModelでの一様流の線形安定性を議論し、さらに不安定なパラメーター領域で数値的に解いて、自然渋滞の形成を議論した。この方程式の定常流に対する解はすぐに計算することができる。系を周期的な長さLの道路としてその中に車がN台あるとすると定常流に対しては
![]() (3.2)
(3.2)
であり、加速度は0であるから解として
![]() (3.3)
(3.3)
が得られる。ここでは初期配置は等間隔に並んでいるとした。これからのゆらぎをyn(t)とし、これが小さいと仮定してその一次の範囲で運動方程式は
![]()
![]() (3.4)
(3.4)
となる。ここで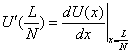 である。これに安定性の解析を行おう。そのため
である。これに安定性の解析を行おう。そのため![]() を代入すると、
を代入すると、
![]()
![]()
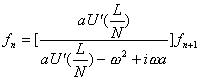 (3.5)
(3.5)
が得られる。この係数の絶対値が1より小さいとき安定である。係数の絶対値を計算し安定条件を計算すると、
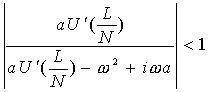
すなわち 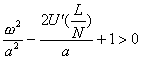 (3.6)
(3.6)
が安定条件である。ω→0の場合
![]() (3.7)
(3.7)
が満たされれば安定である。これは重要な結果である。この式は安定性が車の密度によって変化することを示している。この不安定化が起こった後には定常であった交通流に渋滞流と自由流の粗密波が発生することが数値的な計算から確かめられている。また追従挙動も計算されていて、相空間でリミットサイクルを描くことが分かっている。
一様状態に対して、安定基準は次のように書ける。
(ⅰ)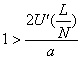 :状態は安定である。
:状態は安定である。
(ⅱ)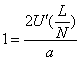 :状態は臨界の状態
:状態は臨界の状態
(ⅲ)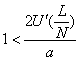 :状態は不安定である。
:状態は不安定である。
上記の基準は任意の速度関数U(h)を持つModelに対して有効である。安定性はドライバーの感度定数aの値と一様状態流(定常解を![]() とする)
とする)![]() の定数車間L/Nと速度関数U(h)の導関数で決まる。
の定数車間L/Nと速度関数U(h)の導関数で決まる。
板東らが行ったsimulationを解説する。
Simulationは4次のルンゲクッタ法を利用している。板東らは、最初に関数Uが
U(h)=tanh(h) (3.8)
である簡単なModelを考えた(図(3.1))。この追従速度関数は3.1章で与えられた特性を持つ。一般性を損なうことなく、式(3.1)のaを1.0とする。まず、車の数をN=100とする。平均車間距離b=L/NはLに依存する。次に、車の初期配置として、車を等間隔に配置し、そのうち1台を前方に0.1だけずらすというやり方で初期の小さな乱れを設定することにより解析する。ここで、車の長さは無視している。また、初速は全車0とする。つまり、
![]() 、for n=0 (3.9)
、for n=0 (3.9)
![]() 、for n≠1 (3.10)
、for n≠1 (3.10)
![]() (3.11)
(3.11)
安定な場合 L=200,N=100
a=1.0
b=L/N=2 (3.12)
f=U′(b)=1-tanh2(b)
=0.077<a/2=1/2 (3.13)
不安定な場合 L=50,N=100
a=1.0
b=L/N=0.5 (3.14)
f=0.876>a/2=1/2 (3.15)
simulationの結果は、図(3.2) と図(3.3)である。これは上記の安定と不安定な場合に対する典型的なModelの時間発展を示している。図(3.2)(安定な場合)において、振幅全ては単調的にtに関して減少していることが分かる。他方、不安定な場合図(3.3) において、正のu-形態の振幅は増加し、一方負のu-形態は減少している。 図(3.4)は車の動きの典型的な振る舞いの例の両方の場合に対して50番目の車の交通距離の時間依存を示している。曲線は時間発展に関して車の移動距離を意味する。安定な場合(点線)で車は定速で動く。すなわち、距離は直線的に増加する。他方、不安定な場合(実線)で移動距離の複雑な振る舞いを見る。つまり、車が後ろへ動く(負の速度で走る)。つまり、車が前の車を通過し、追従速度に従い後ろに動くという非現実的な状況が生じる。1車線Modelを考える限り車同志が通過することは2つの連続する車は衝突することを意味する。これは交通事故が起きることを意味する。このsimulationで微分方程式を差分方程式に置き換え4次のルンゲクッタ法を用いて計算された。このとき、時間のstep⊿tは⊿t=0.1で行ったが、0.1では前の車との相対速度が大きいとき(渋滞の直前)に、この値では大きいために前の車を追い抜いてしまうということが起きている。つまり⊿tを更に小さくしていくと前の車を追い抜く手前で次のstepの計算が始まり、車間距離を計り直すのでぶつからずに走ることができる。しかし、望まれる⊿tの値は決定できない。よってこの簡単なModelは非現実的と見なされる。適切な追従速度関数を選ぶことにより、車がより現実の流れの中で動くよう修正された。
より現実的Modelとして追従速度に対して次の関数を板東らが提案している(図(3.5))。
![]() (3.16)
(3.16)
この場合において、ドライバーは式(3.8)と比べて、徐々に加速と減速をして車を操る。このModelは交通流の予想された振る舞いを与え、式(3.8)で起こっていた事故の代わりに渋滞現象が現れる。また、中立曲線は

で与えられる(図(3.6) )。この現実的Modelより、実際の交通流で見られるような交通渋滞を与える。パラメーターにN=100とL=200を取る。以前のModel(式(3.9)-(3.11))のように同じ初期の乱れを設定する。計算機シミュレーションは時間発展として10000stepまで実行する。図(3.7) は横軸に移動距離、縦軸に速度をとり50台目の車をplotした図である。図(3.7) で明らかに負の速度が現れないことにより、U(h)を(3.11)としたときの問題点が解決されている事が分かる。また、車の速度は時間発展により2つの典型的な値を示す。1つはほとんど0で、他は最高速Umax![]() (2.0)近くである。 図(3.8) は横軸に位置、縦軸に時間をとり10台分の車をplotした図である。図(3.8)に渋滞の5つのクラスターは車のほとんど一様な配置においても存在するとても小さな乱れから形成される様子が見られる。また、どのように渋滞構造が発展するかという過程をみれる。更に図(3.8)は渋滞全てのクラスターがゆっくり同じ速度で後ろに動いていることを示している。この速度
(2.0)近くである。 図(3.8) は横軸に位置、縦軸に時間をとり10台分の車をplotした図である。図(3.8)に渋滞の5つのクラスターは車のほとんど一様な配置においても存在するとても小さな乱れから形成される様子が見られる。また、どのように渋滞構造が発展するかという過程をみれる。更に図(3.8)は渋滞全てのクラスターがゆっくり同じ速度で後ろに動いていることを示している。この速度![]() は、単純に速度U(⊿xmin)と高密集範囲の間隔⊿xminとの間の関係で表される。1stepで渋滞クラスター内の車は全てU(⊿xmin)で進み、1番先頭の車が渋滞クラスターから抜け出し、1番後方に1台車が新しく繋がるという動きをする。つまり、
は、単純に速度U(⊿xmin)と高密集範囲の間隔⊿xminとの間の関係で表される。1stepで渋滞クラスター内の車は全てU(⊿xmin)で進み、1番先頭の車が渋滞クラスターから抜け出し、1番後方に1台車が新しく繋がるという動きをする。つまり、![]() である。高集中地域(渋滞のクラスター)にいて、⊿xminは約0.33で対応する速度U(⊿xmin)は約0.03である。これらの値は全て5クラスターにおいて共通である。他方、低集中地域における間隔⊿xmaxは約3.67で、その地域の速度U(⊿xmax)は約1.88で動く。もし車同志の間隔が2単位長より短いものとして渋滞範囲を定義するなら、渋滞の総数は50で車の総数の約半分である。この結果から、シミュレーションの全体の時間発展が3段階に分割されると理解される。乱れの解析が最初の500(1~500step)のより正しいことがわかる。第2段階(500~7000step)で、各形態の振動は非線形効果により
‘無秩序状態’に見える。最後の段階に入る時間t≧700は渋滞が完全に形成される時間と考える。このことは、渋滞がその時間の前から、その構造を維持することを示す。
である。高集中地域(渋滞のクラスター)にいて、⊿xminは約0.33で対応する速度U(⊿xmin)は約0.03である。これらの値は全て5クラスターにおいて共通である。他方、低集中地域における間隔⊿xmaxは約3.67で、その地域の速度U(⊿xmax)は約1.88で動く。もし車同志の間隔が2単位長より短いものとして渋滞範囲を定義するなら、渋滞の総数は50で車の総数の約半分である。この結果から、シミュレーションの全体の時間発展が3段階に分割されると理解される。乱れの解析が最初の500(1~500step)のより正しいことがわかる。第2段階(500~7000step)で、各形態の振動は非線形効果により
‘無秩序状態’に見える。最後の段階に入る時間t≧700は渋滞が完全に形成される時間と考える。このことは、渋滞がその時間の前から、その構造を維持することを示す。
ここで、車の輸送量を説明する。輸送容量は単位時間で、ある点を通り過ぎる車の数と定義する。一様状態流に対して、渋滞の流れでの輸送の比較をすることができる。Modelの中の渋滞を持つ流れにおいて、輸送容量は次のように計算される。渋滞が完成して、流れはサーキットで高密度と低密度範囲の両方で安定している。車は高密度範囲で低速度U(⊿xmin)で動く。一方、低密度範囲で車は速い速度U(⊿xmax)で動く。大ざっぱに渋滞流の中にいる車の総数と自由流の中にいる車の総数は両方共50である。車の周期Tは
![]() (3.18)
(3.18)
となる。そして、輸送容量は大ざっぱにN/Tとして計算される。ここで、Nはサーキットの車の総数で、Tは上記に与えられる。渋滞の典型的な場合において、すなわち、N=100,L=200で
![]() (3.19)
(3.19)
他方、一様状態流は車間b(=L/N)で一定速度U(b)で動いている。この状況における輸送容量はN/T′でT′=L/U(b)である。N=100,L=200の場合
![]() (3.20)
(3.20)
明らかに渋滞の存在は輸送容量を小さくする。一様な車分配の安定状態の解法において、一度、間隔b(=L/N)を固定し、対応する車の速度U(b)は唯一に(式(3.2))となる。そして、この関数の傾斜f=U′(h)は安定状態流の安定を議論する。初期安定状態流が、bの存在の範囲に依存して安定か不安定かが考えられる。もし、hが安定範囲にあるなら、状態は小さな乱れにおいて影響されないし、交通流の構造は変化せずに残る。他方、もしbが不安定範囲なら、各車は安定範囲から逸脱するように運転される。現実的なModelに対して100台のうち50台は⊿xmin=0.33に近づき、他の車は⊿xmax=3.67に近づく。それは渋滞形態を示す⊿x=0.33の周りの安定範囲の存在である。これに反して、簡単なModelは⊿x![]() 0の周りに安定な範囲を与える。安定な範囲は車が負の速度で動く⊿xmin=-|⊿xmax
|<0の周りである。Model(3.8)は必然的に交通事故を生じる。故に、簡単なModelは‘自然な’渋滞が生じない。そこで、できるだけ簡単な、しかし、自然な交通渋滞を生じる交通流の現実的Modelが考えられた。この現象は運動の運動方程式の非線形効果により表現されたある種の相転移とみなされる。
0の周りに安定な範囲を与える。安定な範囲は車が負の速度で動く⊿xmin=-|⊿xmax
|<0の周りである。Model(3.8)は必然的に交通事故を生じる。故に、簡単なModelは‘自然な’渋滞が生じない。そこで、できるだけ簡単な、しかし、自然な交通渋滞を生じる交通流の現実的Modelが考えられた。この現象は運動の運動方程式の非線形効果により表現されたある種の相転移とみなされる。
simulationは4次のルンゲクッタ法を利用している。交通流における渋滞数について調べる。渋滞数をサーキットの渋滞に属する車の台数と定義する。ある車が渋滞の中にいるかどうかは、車の速度に注目して、![]() ≦0.020であるかにより判別する。
≦0.020であるかにより判別する。![]() ≦0.020であれば、その車は渋滞の中にいるとする。一様流において渋滞数は0である。a=1.0において、渋滞数は図(3.9)となる。 図(3.9) は横軸に密度、縦軸に台数をとり、渋滞数をplotした図である。渋滞数は不安定領域の左側が一番多く、次第に減っていく。ただ、直線的でも単調減少でもなく、少しがたがたとしているのが、渋滞領域の特徴といえる。
≦0.020であれば、その車は渋滞の中にいるとする。一様流において渋滞数は0である。a=1.0において、渋滞数は図(3.9)となる。 図(3.9) は横軸に密度、縦軸に台数をとり、渋滞数をplotした図である。渋滞数は不安定領域の左側が一番多く、次第に減っていく。ただ、直線的でも単調減少でもなく、少しがたがたとしているのが、渋滞領域の特徴といえる。
渋滞は固まりとして動き、自由流も大きく見れば固まりである。つまり、渋滞が発生している状況では、渋滞クラスターと自由流のクラスターとが交互に並んでいる。クラスター数を渋滞の固まりの数と定義する。図(3.10)はa=1.0に対するクラスター数である。図(3.10) は横軸に密度、縦軸に数をとり、クラスター数をplotした図である。クラスター数は渋滞がおおざっぱに安定した後でも変化がある。時間が進むにつれて、2つのクラスタが結びつき1つのクラスターになるということが生じるが、1つのクラスターが2つのクラスターに分離するということはない。 図(3.10)を見ると、stepが進むと、クラスター数が減るところはあるが、クラスター数が増えるところはないのがわかる。しかし、初期配置を変えるとクラスター数は変化する。例えば、b=2.00の場合、timeが20000で渋滞が4つあるが、ここで初期配置を変えてsimulationを行ってみる。つまり、車全体を1,2,3,4,5個の固まりに分けてみる。全ての場合において、Simulationが始まってすぐにクラスター数は1個になり、そこで安定する。つまり、ほぼ等間隔に並べたとき4つのクラスターができたからといって4つがそのbに対する安定状態というわけではない。あるパラメーターでsimulationを行ったとき、クラスター数がより少ない状態が、より安定といえる。
次に流量について調べる。流量は2つの考えで定義する。1つはある時間でのサーキット上の速度を全て足しあげる考え方…①と、もう1つはある位置で一定時間内に通過した車の数を数え上げる考え方…②である。一様流における流量は簡単に議論できる。①の場合、流量は![]() であり、②の場合、一定時間Tの流量は、
であり、②の場合、一定時間Tの流量は、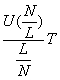 である。渋滞流におけるSimulation結果①②の流量は図(3.11) と(3.12)のようになる。
図(3.11)と図(3.12) は横軸に密度、縦軸に速度の合計や台数をとり、流量をplotした図である。 図(3.11) を見ると、一様流の領域と渋滞流の領域との境で流量が大きく変化する以外はなめらかな曲線である。 図(3.12) の左側から見ていくと、渋滞が起こり始めたところで流量が下がっていることが分かる。渋滞領域に入って、密度が上がるにつれて規則正しく変化せずにがたがたと動いている。これは、それほど長い時間で測定しているわけではないので、測定する時間や場所により流量が変化してしまうためである。これが渋滞領域の特徴である。実際の交通流においてもこのような現象が見られる。
である。渋滞流におけるSimulation結果①②の流量は図(3.11) と(3.12)のようになる。
図(3.11)と図(3.12) は横軸に密度、縦軸に速度の合計や台数をとり、流量をplotした図である。 図(3.11) を見ると、一様流の領域と渋滞流の領域との境で流量が大きく変化する以外はなめらかな曲線である。 図(3.12) の左側から見ていくと、渋滞が起こり始めたところで流量が下がっていることが分かる。渋滞領域に入って、密度が上がるにつれて規則正しく変化せずにがたがたと動いている。これは、それほど長い時間で測定しているわけではないので、測定する時間や場所により流量が変化してしまうためである。これが渋滞領域の特徴である。実際の交通流においてもこのような現象が見られる。
渋滞領域と非渋滞領域はどうなっているのかをaの値を変化させて考察する。a<1.0の領域は負の速度で走っている車が存在する領域である。⊿t=0.1のとき、aは加速と減速を次のstepで最適速度にどれだけの力で変化させるかということであるから、a<1.0のとき前の車との距離が接近してくると減速の効果が現れず衝突してしまう。aの値が小さいため減速の反応が悪くなり、ある車が前の車を追い抜いてしまう(現実は衝突しているが)。追い抜いた車は負の速度で動く(h<0でU(h)<0)ため、その後ろの車は反応が悪い(aが小さいため)上に、前の車が負の速度で近づいてくることにより、追い抜いて(衝突して)しまう。その運動が後ろへ伝播していくので、系の中で1度負の速度が生じてしまうとなかなか消滅しない。その振る舞いが 図(3.13) に表されている。 図(3.13) は横軸に位置、縦軸に時間をとり4台の車をplotした図である。この場合、⊿tを極限まで小さくしていくと、衝突がなくなったがsimulationを実行して議論するのは現実的でない領域である。a≧1.0では負の速度で走っている車が存在せず渋滞流が生じる。a=1.0に固定してb(密度)を1から増やしていく。まず、一様流の状態があり、b=1.15のときに渋滞流に変化する。その後、渋滞流が続き、b=2.80のときにまた一様流になり、その後は一様流である。他のaの値でも相転移が起こる数値は違うもののaを一定にbを動かすと、一様流領域 → 渋滞流領域 → 一様流領域の流れは変わらない。一様流の値の領域に一点だけ渋滞流の値の点が存在することは中立曲線の頂点以外はない。次にb=2.0に固定して、aを1.0から増やしていく。まず、渋滞流があり、a=2.0のところから一様流に変わる。その後はずっと一様流である。他のbの値でも相転移が起こる数値は違うものの渋滞流領域 → 一様流領域の流れは変わらない。渋滞流の値の領域に一点だけ一様流の値の点が存在することはない。いろいろなところでチェックした結果、 図(3.6) で示された曲線の下側が渋滞領域であり、上側が非渋滞領域である事が確かめられた。この結果は式(3.17)と一致している。初期配置をRandomに変化させた(ほぼ等間隔に配置した状態から前後の車とぶつからないぐらい初期位置をずらした)効果を加えたsimulationに対しても渋滞領域と非渋滞領域の範囲が等しいことが確認できた。
渋滞流や一様流というがどのように違いがあるのか。ここで、車間距離の最小値と最大値、![]() と
と![]() はどのような振る舞いをするのか。b=1.6に固定して、aの変化に対して図(3.14)にあるように1.0が一番幅が広く、その後次第に狭くなっていく。図(3.14) は横軸に平均車間距離、縦軸にaをとり
はどのような振る舞いをするのか。b=1.6に固定して、aの変化に対して図(3.14)にあるように1.0が一番幅が広く、その後次第に狭くなっていく。図(3.14) は横軸に平均車間距離、縦軸にaをとり![]() と
と![]() の値をplotした図である。一様流の領域と渋滞流の領域はグラフの違いがはっきりしており、一様流の領域はの幅が無く、渋滞流の領域はあるaに対してはどのbに対しても同じ幅
の値をplotした図である。一様流の領域と渋滞流の領域はグラフの違いがはっきりしており、一様流の領域はの幅が無く、渋滞流の領域はあるaに対してはどのbに対しても同じ幅
![]() を持つ。a=1.0では
を持つ。a=1.0では![]() はほぼ0、
はほぼ0、![]() は2.0に近く、この値を境界としてa<1.0の領域が別の意味を持つことを推測させる。
は2.0に近く、この値を境界としてa<1.0の領域が別の意味を持つことを推測させる。
OV Modelに対して、様々な角度からSimulationを行った。渋滞数と密度との関係は必ずしも直線的でないことが分かり、密度が大きくなるに従いクラスター数は少ない方へ移っていく動きが見られた。しかし、全ての平均車間距離bや初期状態に対してクラスター数が1の状態へ変動するわけではなく、その条件に対する安定状態が存在する。流量についてはdetaの量が多くないので実際の交通流の基本図を再現できたところまではいかなかったが、渋滞領域に見られるがたがたとした領域が現れたことは確認できた。横軸に平均車間距離、縦軸にaをとった平面における渋滞領域と非渋滞領域の安定性に関する理論解析とSimulationの一致は見られた。また、渋滞の幅は、渋滞と非渋滞を決める一つの目安である。![]() が幅を持っていれば渋滞で、ほぼ0なら非渋滞とした。しかし、図(3.8)
のようなplotをしてみると見かけでは渋滞と非渋滞を判断しづらいものもある。例えば、図(3.15)
と(3.16)はa=1.9,b=2.0でのグラフであるが、図(3.15)では渋滞と判断できるが、 図(3.16) では渋滞とは判断しづらい。
図(3.15) は横軸に位置、縦軸に時間をとり車をplotした図で、 図(3.16)
は横軸に移動距離、縦軸に速度をとり50台目の車をplotした図である。渋滞領域での車の速度はaの値が大きくなるほど
が幅を持っていれば渋滞で、ほぼ0なら非渋滞とした。しかし、図(3.8)
のようなplotをしてみると見かけでは渋滞と非渋滞を判断しづらいものもある。例えば、図(3.15)
と(3.16)はa=1.9,b=2.0でのグラフであるが、図(3.15)では渋滞と判断できるが、 図(3.16) では渋滞とは判断しづらい。
図(3.15) は横軸に位置、縦軸に時間をとり車をplotした図で、 図(3.16)
は横軸に移動距離、縦軸に速度をとり50台目の車をplotした図である。渋滞領域での車の速度はaの値が大きくなるほど![]() の値は大きくなるので、x-t平面でグラフを書いたときに渋滞のクラスターを示す黒い帯のような模様が見えづらくなってしまう。これを渋滞領域と言っていいのかということだが、現実でも渋滞には大きな渋滞、小さな渋滞があるのでこのような見かけの上では分かりづらいものが存在してもおかしくはない。また、
の値は大きくなるので、x-t平面でグラフを書いたときに渋滞のクラスターを示す黒い帯のような模様が見えづらくなってしまう。これを渋滞領域と言っていいのかということだが、現実でも渋滞には大きな渋滞、小さな渋滞があるのでこのような見かけの上では分かりづらいものが存在してもおかしくはない。また、![]() の幅があるbの値から突然変化(相転移)する値が存在することは重要であり、その値が渋滞領域と非渋滞領域の境目とするのが適当である。
の幅があるbの値から突然変化(相転移)する値が存在することは重要であり、その値が渋滞領域と非渋滞領域の境目とするのが適当である。
4. UV Model
4.1 Modelの紹介
ここでOV Modelを改良して単純ではあるが、より一般的な最適速度Modelが早川・中西により提案されている。[17]これをUV Modelと呼ぶ。
![]()
![]() (4.1)
(4.1)
Xn(t)はn番目の位置、aはドライバーの反応を意味するパラメーターである。このModelはドライバーの心理的な効果を含んでいる。すなわち、前方の距離![]() ばかりでなく、後方の距離
ばかりでなく、後方の距離![]() も関係している。追従速度関数
も関係している。追従速度関数![]() は
は![]() の距離の単調増加であり、
の距離の単調増加であり、![]() は
は![]() の距離の単調減少関数であり、車間距離が十分大きいと1に漸近する。車間距離が詰まると1よりVが大きくなり、加速(あおりのよりアクセルを踏む)の効果が働くというものである。そして、具体的には
の距離の単調減少関数であり、車間距離が十分大きいと1に漸近する。車間距離が詰まると1よりVが大きくなり、加速(あおりのよりアクセルを踏む)の効果が働くというものである。そして、具体的には
![]() (4.2)
(4.2)
を適応する(図(4.1) )。![]() は定数である。追従速度Modelの関数として方程式(4.1)は、UVの積の形になっているので、
は定数である。追従速度Modelの関数として方程式(4.1)は、UVの積の形になっているので、![]() のドライバーは
のドライバーは![]() の距離が短いときに十分な前方との距離がないとVの関数の効果がそれほど現れず車がVの関数の効果により衝突することは防がれている。方程式(4.2)で記述されるこのModel(4.1)は板東らにより提案されたOV
Model
の距離が短いときに十分な前方との距離がないとVの関数の効果がそれほど現れず車がVの関数の効果により衝突することは防がれている。方程式(4.2)で記述されるこのModel(4.1)は板東らにより提案されたOV
Model
![]() (4.3)
(4.3)
の一般化である。
4.2 Modelの解析
まず、一様伝播流の線形安定性の解析をまとめる。![]() 一定である定常伝播流が存在することを観察する。式(4.1)をもう一度見てみると
一定である定常伝播流が存在することを観察する。式(4.1)をもう一度見てみると
![]() (4.4)
(4.4)
hは系により決まる平均車間距離で![]() である。
である。![]() の周りの線形化された式(4.4)は
の周りの線形化された式(4.4)は
h![]() 0,(h≪1)の周りでのTaylor展開
0,(h≪1)の周りでのTaylor展開
![]() を使い、1次まで取ると、
を使い、1次まで取ると、
![]()
![]()
![]()
![]() (4.5)
(4.5)
フーリエ変換を使って
![]() (4.6)
(4.6)
q=2πm/Nhで車の総数N。式(4.5)を書き直すと、
![]() (4.7)
(4.7)
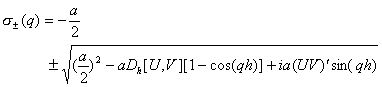 (4.8)
(4.8)
UやVの独立変数に落ちる。![]() はHirotaの導関数を表す。初期値問題(4.7)の解は
はHirotaの導関数を表す。初期値問題(4.7)の解は
![]()
![]()
同様にして ![]()
これらは ![]() の解である。
の解である。
![]()
である。つまり、![]() と
と![]() に比例する項の線形結合である。
に比例する項の線形結合である。![]() の比例形態は早く衰退する形態として解釈される。ところが一方
の比例形態は早く衰退する形態として解釈される。ところが一方![]() の比例項は遅く、より重要な形態である。同様な解法(4.5)の線形安定性の違反(ここでは、
の比例項は遅く、より重要な形態である。同様な解法(4.5)の線形安定性の違反(ここでは、![]() は減少すると仮定している。)は
は減少すると仮定している。)は![]() に同値である。ここで
に同値である。ここで![]() は
は![]() の実数部分である。qh≠0を仮定すると(qh=0は中立形態)、不安定状態は
の実数部分である。qh≠0を仮定すると(qh=0は中立形態)、不安定状態は
逆フーリエ変換 ![]() を利用する。
を利用する。
![]()
![]()
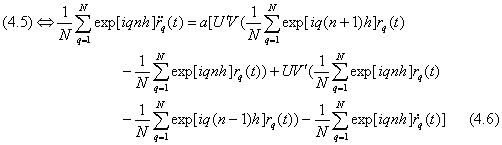
(4.6)が成り立つためには両辺の各項どうしが等しくならなくてはいけない。
故に ![]()
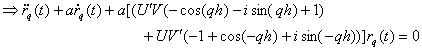
![]()
![]() (4.7)
(4.7)
により与えられる。そして、もっとも不安定な形態はqh→0で存在し、長波長(ω→0)に対する中立曲線は
![]() (4.8)
(4.8)
により与えられる。パラメーター空間(a,h)での中立曲線は式(4.2)でf0=a/[1+tanh(2)]に対して 図(4.2) に示されている。
4.3 Simulation
simulationは4次のルンゲクッタ法を利用している。以前のModel(式(3.12)-(3.14))のように同じ初期の乱れを設定する。ここでも車の長さは無視している。計算機シミュレーションは時間発展として10000stepまで実行する。 図(4.3) でも明らかに負の速度が現れない。
図(4.3) は横軸に移動距離、縦軸に速度をとり50台目の車をplotした図である。また、車の速度は時間発展として2つの典型的な値を示す。1つはほとんど0で、他は最高速Umax近くである。 図(4.4) から渋滞の5つのクラスターは、車のほとんど一様な分配において存在するとても小さな乱れから形成される。また、どのように渋滞構造が発展するかという過程をみれる。更に 図(4.4) は渋滞全てのクラスターがゆっくり同じ速度で後ろに動いていることを示している。この速度![]() は、単純に速度U(⊿xmin)V(⊿xmin)と高密集範囲の間隔⊿xminとの間の関係で表される。1stepで渋滞クラスター内の車は全てU(⊿xmin)V(⊿xmin)で進み、1番先頭の車が渋滞クラスターから抜け出し、1番後方に1台車が新しく繋がるという動きをする。つまり、
は、単純に速度U(⊿xmin)V(⊿xmin)と高密集範囲の間隔⊿xminとの間の関係で表される。1stepで渋滞クラスター内の車は全てU(⊿xmin)V(⊿xmin)で進み、1番先頭の車が渋滞クラスターから抜け出し、1番後方に1台車が新しく繋がるという動きをする。つまり、![]() となる。高集中地域(渋滞のクラスター)にいて、⊿xminは約0.37で対応する速度U(⊿xmin)V(⊿xmin)は約0.08である。これらの値は全て5クラスターにおいて共通である。他方、低集中地域における間隔⊿xmaxは約2.29で、その地域の速度U(⊿xmax)は約2.20で動く。この結果から、シミュレーションの全体の時間発展が3段階に分割される。乱れの解析が最初の700(1~700step)のより正しいことがわかる。第2段階(700~6000step)で、各形態の振動は非線形効果により‘無秩序状態’に見える。最後の段階に入る時間t≧600は渋滞が完全に形成される時間と考える。このことは、渋滞がその時間の前から、その構造を維持することを示す。
となる。高集中地域(渋滞のクラスター)にいて、⊿xminは約0.37で対応する速度U(⊿xmin)V(⊿xmin)は約0.08である。これらの値は全て5クラスターにおいて共通である。他方、低集中地域における間隔⊿xmaxは約2.29で、その地域の速度U(⊿xmax)は約2.20で動く。この結果から、シミュレーションの全体の時間発展が3段階に分割される。乱れの解析が最初の700(1~700step)のより正しいことがわかる。第2段階(700~6000step)で、各形態の振動は非線形効果により‘無秩序状態’に見える。最後の段階に入る時間t≧600は渋滞が完全に形成される時間と考える。このことは、渋滞がその時間の前から、その構造を維持することを示す。
交通流における渋滞数について調べる。ある車が渋滞の中にいるかどうかは、車の速度に注目して、![]() ≦0.080であるかにより判別する。
≦0.080であるかにより判別する。![]() ≦0.080であれば、その車は渋滞の中にいるとする。一様流において渋滞数は0である。a=1.0において、渋滞数は 図(4.5) となる。 図(4.5)
は横軸に密度、縦軸に台数をとり、渋滞数をplotした図である。渋滞数は不安定領域の左側が一番少なく、次第に増えていく。ただ、直線的でも単調減少でもなく、少しがたがたとしているのが、渋滞領域の特徴といえる。次に渋滞クラスター数を調べてみる。 図(4.6) はa=1.0に対するクラスター数である。
図(4.6) は横軸に密度、縦軸に数をとりクラスター数をplotした図である。クラスター数は渋滞がおおざっぱに安定した後でも変化がある。ここでも、時間が進むにつれて、2つのクラスターが結びつき1つのクラスターになるということが生じるが、1つのクラスターが2つのクラスターに分離するということはない。 図(4.4) を見ると、stepが進むと、クラスター数が減るところはあるが、クラスター数が増えるところはないのがわかる。しかし、初期配置を変えるとクラスター数は変化する。例えば、b=1.60の場合、timeが20000で渋滞が5つあるが、ここで初期配置を動かしてsimulationを行ってみる。つまり、車全体を1,2,3,4,5個の固まりに分けてみる。全ての場合、Simulationが始まってすぐにクラスター数は1個になり、そこで安定する。つまり、ほぼ等間隔に並べたとき5つのクラスターができたからといって5つがそのbに対する安定状態というわけではないが、あるパラメーターでsimulationを行ったとき、クラスター数が少ない状態が、より安定といえる。
≦0.080であれば、その車は渋滞の中にいるとする。一様流において渋滞数は0である。a=1.0において、渋滞数は 図(4.5) となる。 図(4.5)
は横軸に密度、縦軸に台数をとり、渋滞数をplotした図である。渋滞数は不安定領域の左側が一番少なく、次第に増えていく。ただ、直線的でも単調減少でもなく、少しがたがたとしているのが、渋滞領域の特徴といえる。次に渋滞クラスター数を調べてみる。 図(4.6) はa=1.0に対するクラスター数である。
図(4.6) は横軸に密度、縦軸に数をとりクラスター数をplotした図である。クラスター数は渋滞がおおざっぱに安定した後でも変化がある。ここでも、時間が進むにつれて、2つのクラスターが結びつき1つのクラスターになるということが生じるが、1つのクラスターが2つのクラスターに分離するということはない。 図(4.4) を見ると、stepが進むと、クラスター数が減るところはあるが、クラスター数が増えるところはないのがわかる。しかし、初期配置を変えるとクラスター数は変化する。例えば、b=1.60の場合、timeが20000で渋滞が5つあるが、ここで初期配置を動かしてsimulationを行ってみる。つまり、車全体を1,2,3,4,5個の固まりに分けてみる。全ての場合、Simulationが始まってすぐにクラスター数は1個になり、そこで安定する。つまり、ほぼ等間隔に並べたとき5つのクラスターができたからといって5つがそのbに対する安定状態というわけではないが、あるパラメーターでsimulationを行ったとき、クラスター数が少ない状態が、より安定といえる。
次に流量について調べる。ここでも、流量は2つの考え方(ある時間でのサーキット上の速度を全て足しあげる考え方…①、ある位置で一定時間内に通過した車の数を数え上げる考え方…②)を用いる。一様流における流量は簡単に議論できる。①の場合、流量は![]() であり、②の場合、一定時間Tの流量は、
であり、②の場合、一定時間Tの流量は、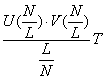 である。渋滞流におけるSimulation結果①②の流量は
図(4.7)と(4.8) のようになる。 図(4.7) と 図(4.8) は横軸に密度、縦軸に速度の合計や台数をとり、流量をplotした図である。 図(4.7) を見ると、一様流の領域と渋滞流の領域との境で流量が大きく変化する以外はなめらかな曲線である。これも一様流の曲線と渋滞流の曲線を結んだようにも見える。 図(4.8) の左側から見ていくと、渋滞が起こり始めたところで流量が下がっていることが分かる。渋滞領域に入って、密度が上がるにつれて規則正しく変化せずにがたがたと動いている。測定時間が短いので、渋滞領域のように流量が一定しない故に起こる渋滞領域の特徴である。実際の交通流においてもこのような現象が見られる。
である。渋滞流におけるSimulation結果①②の流量は
図(4.7)と(4.8) のようになる。 図(4.7) と 図(4.8) は横軸に密度、縦軸に速度の合計や台数をとり、流量をplotした図である。 図(4.7) を見ると、一様流の領域と渋滞流の領域との境で流量が大きく変化する以外はなめらかな曲線である。これも一様流の曲線と渋滞流の曲線を結んだようにも見える。 図(4.8) の左側から見ていくと、渋滞が起こり始めたところで流量が下がっていることが分かる。渋滞領域に入って、密度が上がるにつれて規則正しく変化せずにがたがたと動いている。測定時間が短いので、渋滞領域のように流量が一定しない故に起こる渋滞領域の特徴である。実際の交通流においてもこのような現象が見られる。
渋滞領域と非渋滞領域の範囲はどうなっているのだろうか。図(4.9) を見てみると、a<1.0についても印が入っているが、この領域では負の速度で走っている車が存在する領域である。 図(4.9) は横軸に平均車間距離、縦軸にaをとり渋滞か非渋滞かをplotした図である。a≧1.0では負の速度で走っている車が存在せず渋滞流が生じる。a=1.0に固定してb(密度)を0.5から増やしていく。まず、一様流の状態があり、b=0.80のときに渋滞流に変化する。その後、渋滞流が続き、b=2.20のときにまた一様流になり、その後は一様流である。他のaの値でも相転移が起こる数値は違うものの一様流領域 渋滞流領域 → 一様流領域の流れは変わらない。一様流の値の領域に一点だけ渋滞流の値の点が存在することは中立曲線の頂点以外はない。次にb=1.6に固定して、aを0から増やしていく。まず、渋滞流があり、a=2.05のところから一様流に変わる。その後はずっと一様流である。他のbの値でも相転移が起こる数値は違うものの渋滞流領域 → 一様流領域の流れは変わらない。渋滞流の値の領域に一点だけ一様流の値の点が存在することはない。いろいろなところでチェックした結果、式(4.9)で示された曲線での渋滞領域と非渋滞領域の範囲とは一致しない結果となる。初期配置にrandomの効果を入れてみた。Simulationにおける結果との一致によりrandomの初期配置に関する安定性は見られたが、式(4.8)とは一致しない結果となった。
UV Modelでの渋滞流と一様流の違いはどこにあるのか。ここで、![]() と
と![]() はどのような振る舞いをするのか。b=1.6に固定して、aの変化に対して 図(4.10) にあるように1.0が一番幅が広く、その後次第に狭くなっていく。 図(4.10)は横軸に平均車間距離、縦軸にaをとり、
はどのような振る舞いをするのか。b=1.6に固定して、aの変化に対して 図(4.10) にあるように1.0が一番幅が広く、その後次第に狭くなっていく。 図(4.10)は横軸に平均車間距離、縦軸にaをとり、![]() と
と![]() の値をplotした図である。一様流の領域にはいると上限の値が消え、下限の値が次第に上がっていく。一様流の領域と渋滞流の領域はグラフの違いがはっきりしており、一様流の領域はの幅が無く、ほとんど0であるのに対し、渋滞流の領域は一定のaに対してはどのbに対しても同じ幅
の値をplotした図である。一様流の領域にはいると上限の値が消え、下限の値が次第に上がっていく。一様流の領域と渋滞流の領域はグラフの違いがはっきりしており、一様流の領域はの幅が無く、ほとんど0であるのに対し、渋滞流の領域は一定のaに対してはどのbに対しても同じ幅
![]() を持つ。
を持つ。
4.4 まとめ
UV Modelに対して、OV Modelと同じようにSimulationを行ってみた。UV Modelにおいても渋滞数は密度との関係は必ずしも直線的でないことが分かり、simulation時間が増えるとクラスター数は少ない方へ移っていく動きが見られたが、全ての密度や初期状態に対してクラスター数が1へ行くわけではなく、その条件に対する安定状態が存在する。流量についてはdetaの量が多くないので実際の交通流の基本図を再現できたところまではいかなかったが、渋滞領域に見られるがたがたとした領域が現れたことは確認できた。横軸に平均車間距離、縦軸にaをとった平面における渋滞領域と非渋滞領域の理論とSimulationの不一致が見られた。また、速度の幅は、渋滞と非渋滞を決める一つの目安である。![]() が幅を持っていれば渋滞領域で、ほぼ0なら非渋滞領域としていた。しかし、
図(4.3) のようなplotをしてみると見かけでは渋滞と非渋滞を判断しづらいものもある。例えば、
図(4.11) と(4.12) はa=2.0,b=1.6でのグラフであるが、 図(4.12) では渋滞と判断できるが、 図(4.11)
では渋滞とは判断しづらい。 図(4.11) は横軸に位置、縦軸に時間をとり車をplotした図である。 図(4.12) は横軸に移動距離、縦軸に速度をとり、50台目の車をplotした図である。渋滞領域での車の速度はaの値が大きくなるほど
が幅を持っていれば渋滞領域で、ほぼ0なら非渋滞領域としていた。しかし、
図(4.3) のようなplotをしてみると見かけでは渋滞と非渋滞を判断しづらいものもある。例えば、
図(4.11) と(4.12) はa=2.0,b=1.6でのグラフであるが、 図(4.12) では渋滞と判断できるが、 図(4.11)
では渋滞とは判断しづらい。 図(4.11) は横軸に位置、縦軸に時間をとり車をplotした図である。 図(4.12) は横軸に移動距離、縦軸に速度をとり、50台目の車をplotした図である。渋滞領域での車の速度はaの値が大きくなるほど![]() の値は大きくなるので、x-t平面でグラフを書いたときに渋滞のクラスターを示す黒い帯のような模様が見えづらくなってしまう。これを渋滞領域と言っていいのかということだが、現実でも渋滞には大きな渋滞、小さな渋滞があるのでこのような見かけの上では分かりづらいものが存在してもおかしくはない。また
の値は大きくなるので、x-t平面でグラフを書いたときに渋滞のクラスターを示す黒い帯のような模様が見えづらくなってしまう。これを渋滞領域と言っていいのかということだが、現実でも渋滞には大きな渋滞、小さな渋滞があるのでこのような見かけの上では分かりづらいものが存在してもおかしくはない。また![]() の幅があるbの値から突然変化(相転移)する値が存在することは重要であり、その値が渋滞領域と非渋滞領域の境目とするのが適当である。
の幅があるbの値から突然変化(相転移)する値が存在することは重要であり、その値が渋滞領域と非渋滞領域の境目とするのが適当である。
5. まとめと考察
この論文では追従モデルの中でもOV ModelとUV Modelを中心に議論してきた。OV Modelについて、渋滞での車の振る舞いを解析した。渋滞領域での流量の振る舞いや渋滞数の変化、またはクラスター数の安定状態などModelの特徴を理解した。渋滞領域と非渋滞領域をわける中立曲線に対する理論の解析とsimulationでの結果が一致した。また、random初期配置に対するModelの安定性も確認できた。UV ModelはOV Modelの運動方程式と、関数形はそれほど変わらない。それ故、あおりの効果により低速が引き上げられはするが、サーキットにおける車の車間距離による加速と減速の振る舞いや、渋滞領域での流量が、がたがたとする変化などは見られる。しかし、渋滞と非渋滞の領域は理論から求めた式(4.8)とsimulationとは一致せず、その理由は分かっていない。Simulationから調べたdataを見ると、式(4.8)の上に渋滞と非渋滞を分ける中立曲線が存在するように見える。なぜsimulationが理論の解析からずれてしまったのか、もしくはsimulationのdataに一致する曲線が存在するのかと、Modelの2車線化への移行がこれからの課題である。
6. 参考論文
7. プログラム : ただし「絵」です。ご利用あるいはご入用の方はご連絡ください。