マルチアノード光電子増倍管における少光量出力の研究
原田智也、竹下徹 :mail tohru@shinshu-u.ac.jp
信州大学理学部物理学科
1996/Feb
目的
この研究は、光電子増倍管に微弱な光子を入射したときの出力パルスを観測し、最終的には一個の光電子を捕捉したときのパルス波形を解析することを目的とす
る。
光電子増倍管は微弱な光の強弱を光電効果によって光電子に置き換え、それを増幅することによって各種分析に利用できるデータを得るためのデバイスである。
高エネルギー物理学の分野では、高エネルギー粒子によるチェレンコフ放射の観測や、放射線が当たることで蛍光を発する物質を用いたシンチレーションカウン
ターなどに必要不可欠な検出装置である。
これらの実験では、大抵の場合入射光量が非常に小さくなる。光電子増倍管は、その構造上一個、二個といった非常に微量な光電子の検出も可能であるが、その
際、数が多いときは見ることのできなかった光電子の離散的な構造が出力波形に現われると思われる。その波形から、逆に正確な入射光電子量を求めてみる。
また電磁シャワーカロリメーターにおける位置測定精度の研究は、電磁シャワー出発位置を知ることにほかならない。しかしながら電磁シャワーはその始まりで
の粒子数すなわち測定器に落とすエネルギーは少ない。このため測定器内のエネルギーを光に変換して電磁シャワーを測定するシステムでは微小な光量での位置
測定という2重の問題を抱え込むこととなる。ここでは位置測定を目指すために導入するファインメッシュ光電子増倍管の微小光量に対する反応を研究する。こ
こでは浜松ホトニクス社製のR2486というマルチアノード型の光電子増倍管の出力信号について入力される光量が極く微小な場合の研究を行った。
実験装置
光電子増倍管の(PhotoMultiplier
Tube 以下PMT)への入射光量を正確に制御できるシステムの構築を行った。光源としては発光ダイオード(Light
Emitting Diode 以下LED)を用い、波長によらない減衰をするフィルター(Neutral
Density Filter : ND
Filter)を光源とPMTの間にはさみ入射光量等を変化させたときの出力波形を測定、解析することのできるシステムである。その概念図を示す。LED
-DrivePluseとGatePulseは完全の同期のとれた信号である。それぞれ幅100ns,300nsである。LEDとPMTの間におかれる
ND-filterはFUJIFILM社製の減光フィルターND01.-0.3を重ねて用いた。また、光束をある程度しぼり込んでおくためにも、LEDと
filterとの間は短い光ファイバーケーブルを通して結んである。この装置は、「マルチアノード光電子増倍管の位置測定精度の研究」で用いられた物と同
一である。なおPMTによる実際の測定部分は、完全な暗中に置かれている(図の暗い箱部分)。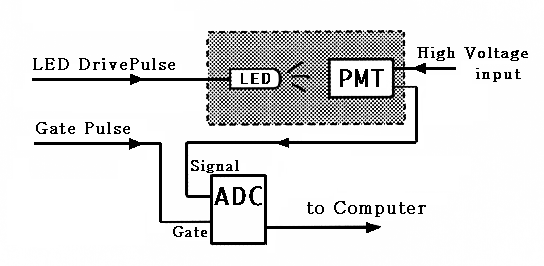
この装置を用いてSignalとGate-pulseの典型的例を下図に示す。このときは充分光量を減らしているため1個1個の光子による電気シグナルパ
ルスが別々に見えている。
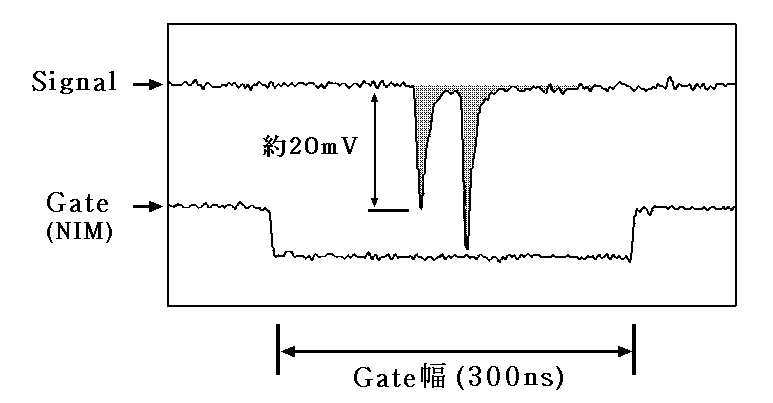
オシロスコープの画面のハードコピーから光電子増倍管の暗電流によるノイズが充分小さいことが解る。
入射光量の減衰テスト
入射光量と出力波高分布の関係を述べたが実際明らかにその入射光量が充分小さく光電面における光電子数が平均1個程度であることを実験でに確かめておく必
要がある。このために普通光電子数を数えることのできるボックスアンドグリッド型あるいはLinear-Forcused
type
の光電子増倍管(浜松ャzトニクス社製のR1332)を用いてsingle-photoelecctronの観測実験を行った。装置はすでに述べた物であ
り、PMTをR1332に変えた。この光電子増倍管はN=12段で最大印可電圧2.7KV,typical
gain = 1x10^6である。
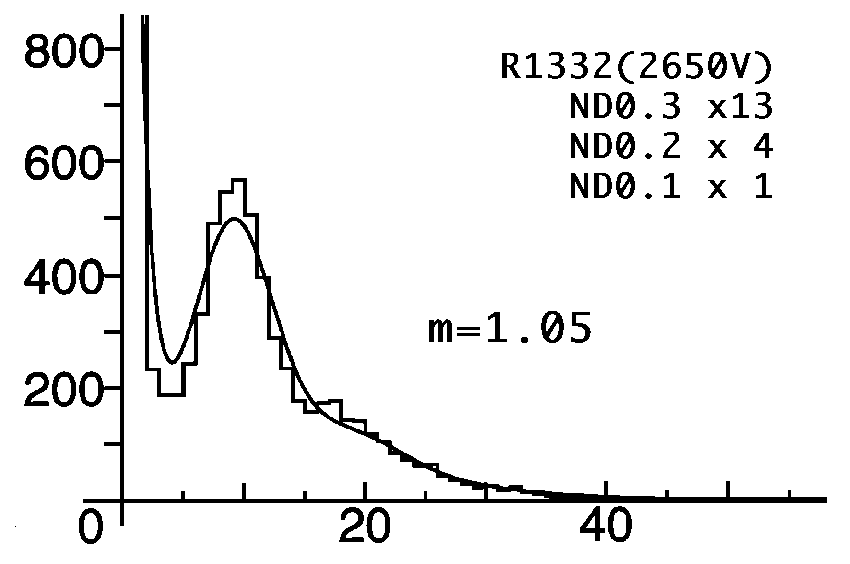
図はND-filter 0.3 を12枚、0.2を4枚、0.1を1枚の場合と光量をその半分にしたND-filter 0.3
を13枚、0.2を4枚、0.1を1枚の場合について波高分布を示した。
図中のmは複数のPoisson分布の重みつきの平均値である。
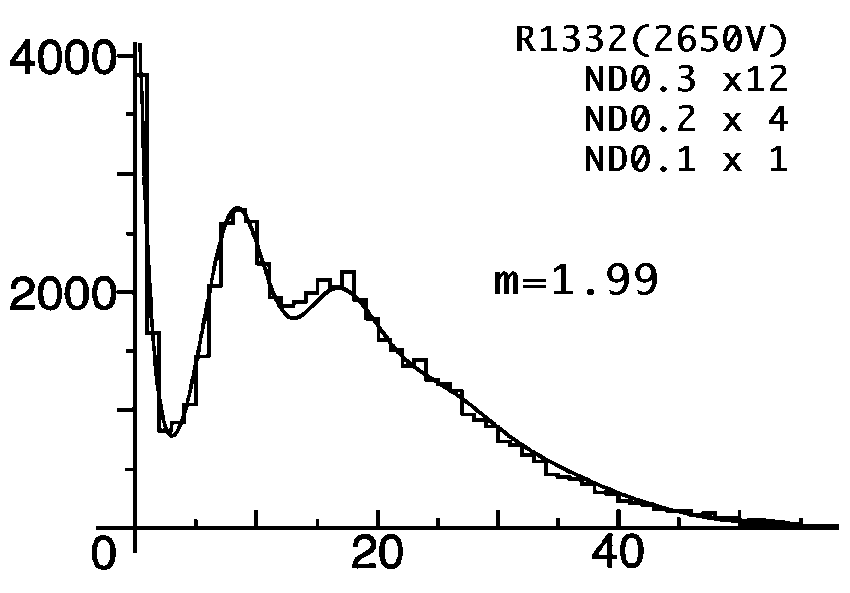
図で2つの山の位置(電荷量分布のピーク位置)を測ると、ちょうど一つ目の山の二倍の位置に二つ目の山のピークが来ている。すなわちこれがf式におけるn
=1とn=2のGauss分布と考えるのが自然である。測定されたグラフを、Gauss関数でfittingして、おのおのの平均値(x)とsから二次電
子増幅率dを求めてみた。それぞれn=1,n=2に対応してd=9.6
(n=1), d=7.2(n=2)
と言う結果であった。すなわち今まで仮定してきた二次電子増幅率dが光電子増倍管の全てのダイノード段で等しいという仮定に問題があることが判明する。
ダイノードの各段での電位差はホトニクス社[1]の資料より解っているので、 ここでは、経験則として二
次電子増幅率dの電圧依存性はd=AE^aとして扱う。ここでAは定数、Eはダイノード間電圧、aはダイノードの特性荷よって決まる値で0.7-0.8を
とる。
ここでは、経験則として二
次電子増幅率dの電圧依存性はd=AE^aとして扱う。ここでAは定数、Eはダイノード間電圧、aはダイノードの特性荷よって決まる値で0.7-0.8を
とる。
各段にかかる電圧は、全体としてかけた電圧にこの値の全体に対する割合をかけることで得られ、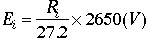 各段間の電圧比)と表わさ
れる。2650とは本実験で全体としてかけた電圧である。よって、各ダイノード段でのdの値は、
各段間の電圧比)と表わさ
れる。2650とは本実験で全体としてかけた電圧である。よって、各ダイノード段でのdの値は、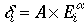
となる。ここでa=0.8をとり、Aは未知としておく。光電子増倍管の増幅率Gは、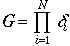 で与えられ、また相対変動
は、
で与えられ、また相対変動
は、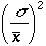
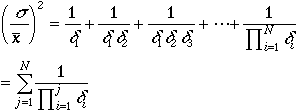
.
ここでグラフよりG=1.5x 10^7,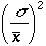 =0.1と読み取ると、未知数A=0.0654と決まるので、このAを
用いて再度各ダイノード段における電圧勾配の違いを考慮にいれた増幅率と相対変動を計算すると、
=0.1と読み取ると、未知数A=0.0654と決まるので、このAを
用いて再度各ダイノード段における電圧勾配の違いを考慮にいれた増幅率と相対変動を計算すると、
G=1.565x10^7,
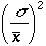 =0.1482
=0.1482
という値を得る。これを用いて改めて波高分布に対してfitting を行う。このときparameterはx,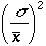 ,m(平均光電子数)である。また電荷分布のゼロ付近のペデスタルのしみだしは、exp(a-bx)関数でfitした。
,m(平均光電子数)である。また電荷分布のゼロ付近のペデスタルのしみだしは、exp(a-bx)関数でfitした。
ND-filetを交換することによる光量の相対変化は、ND一枚につき0.3倍というメーカー値と全く一致しており、mの値は充分に信頼できるものと考
えられる。
fittingの結果はすでに図中に同時に示めされている。
これによりLED光源に複数枚のND-filetをかけて光量を減らし0.3
を13枚、0.2を4枚、0.1を1枚の場合平均光電子数はほぼ1個を達成できることが確かめられた。
single photoelectronの検出シミュレーション
PMTに入る光量が十分に小さいとき、出力の分布がどのようになるか考えてみる。たとえ十分に注意して光量を一定に保ったとしても、光子の入射は当然確率
的な分布を持つ。もしも確実に一定数の光子が入射したとしても、光電面から放出される光電子はやはりある分布を持つことになる。このような少数かつ離散的
な数を扱う統計現象では、その分布はPoisson分布
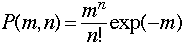
に従うということが知られている。ここでmは取り扱う光電子の平均数、nは実際に起きる値である。この分布は、mが十分大きい極限ではGauss分布に一
致する。このように発生する光電子が既にある程度の分散をしているのであるが、それとは別にPMTのなかで増幅されていく過程でも、増幅率の周りに確率的
な分布をする。つまり全体の増幅率をGとすると、1個の光電子が最終的にG個の電子になったり、G+1個の電子になったり、という形の分布である。この両
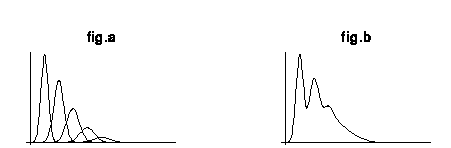
者の分散関係を考慮すれば、図aのような形の確率分布をするであろう。この図の一つ一つの山は入射光電子の1個2個...に対応し、それぞれの山の広がり
が増幅される過程でのばらつきに相当する。十分に入射光電子数の大きいところでは、1個の違いは非常に微々たるものであるが、1個と2個の間ではその違い
はとても大きい。つまり山と山の間隔が相対的に大きくなるので、入射光電子の平均数が一個、などというところでは全体として図bのような離散的な構造の観
測が期待される。
データ取得はCAMAC,GPIBを用いたすでに述べられたシステムでPersonal
computerにより1パルス毎にADCにより電流を時間積分して電荷量を測定する方法で行った。PMTへの入射光量が比較的多い時の典型的なパルス高
分布を示す。
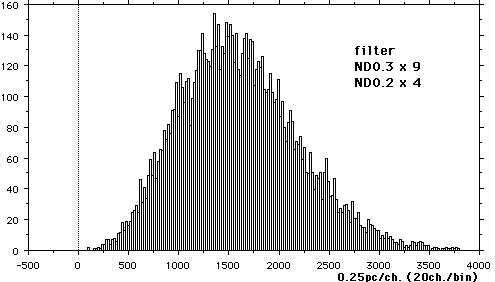
ここでパルス高分布(各光信号毎の光電子増倍管の出力信号が含む電荷のヒストグラム:横軸は電荷、縦軸は頻度)の幅は、前に述べた2つのばらつき、入射光
電子のPoisson分布とPMT内部で増幅される過程でのばらつきを含む。後者は、電子がダイノードにぶつかって二次電子を放出する時に、例えば二次電
子増幅率d=5を持つダイノードであれば、一個の電子が入射すれば平均5個の電子が放出されると考えられる。しかし、これはあくまでも統計的な現象であ
り、実際に出てくる電子は4個かもしれないし、6個かもしれない。そのばらつきはPoisson分布に従うと考えられる。ただしPoisson分布は平均
が1や2といった小さい数のときには左右非対称の特徴的な分布を見せるが、平均が5程度になるとほとんどGauss分布と同じ形を見せるようになる。よっ
て各段における分布は、Poisson分布における s=sqrt(x
)(ここでxは分布の平均値)を持った形のGauss分布を考えることにする。さらにn個の光電子が一段目のダイノードに飛び込んできたとき、発生する二
次電子の確率分布を考えてみよう。二次電子増幅率をdとすると、その分布の平均値はndとなり、相対変動 (s1/x1^2) は 1/(nd)
となる。次にその確率分布を持った電子が二段目のダイノードに入射する。すべてのダイノードが同じ増幅率 d
であるならば、二段目のダイノードから発生する電子の平均数はnd2となり、相対変動 (s2/x2^2)は二段目のばらつき1/(nd^2)に一段目の
ばらつきを加え、1/(nd)
+ 1/(nd^2) となる。よって、最終的にN段のダイノードを経て陽極に達した電子の平均数は1/(nd^N)、相対変動は
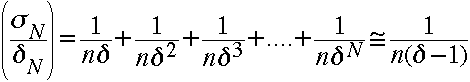
となる
Nの段数は、いまのところ10段以上のものを考えているので、この近似式は十分な精度で成り立っていると考えてよい。
とすると、陽極で観測される電子の確率分布は次のような標準偏差s
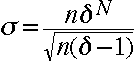
を持つガウス分布になるであろう。まとめると次のようになる。
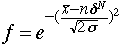
さて、ここで一段目のダイノードに入射する光電子の数のばらつきを考慮する。平均数一個という光電子を観測しようというのであるから、入射する光電子の数
はPoisson分布に従う。先にn個の光電子が入射したときの陽極での電子の確率分布を見たが、実際にはnの値を少しずつ変えたたくさんのガウス分布の
重ね合せで描かれるべきである図b。例えば平均入射数が1であるとしよう。 すると実際に入射する光電子の割合はpoisson分布の式より、1個である
確率 1/eに対して2個の確率が1/(2e)、つまり1/2、3個の確率が1/(6e)、同じく1/6となる。この入射数の分布は、最終的なアノードで
の分布fのどこに現われるかというと、統計的に積み重ねた時の事象数、つまりは各ガウス分布の積分値となるはずである。fの積分値はsqrt(2pai)
*sとなるので、最終的にこれらの関係式をまとめると、アノードに現われる電子の確率分布は
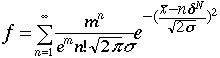
というガウス分布の重ね合せで描かれるはずである。
これらの未知数のうち、Nはダイノードの段数であるから、PMTに固有の値が一意にきまる。d
は電圧によって変化するので正確な値は分からないが、カタログスペックの増幅率G=dNと仮定すると、今回実験で使ったものも含め、一般的なPMTにおけ
るdの値は2〜5程度である。そこで、N=12段、d=5としてグラフを描いてみた。(図で左はm(光電子の平均数)=1の時のn=1〜5の分布とその重
ね合せ。右はm=10の時のn=1〜10の重ね合せ)
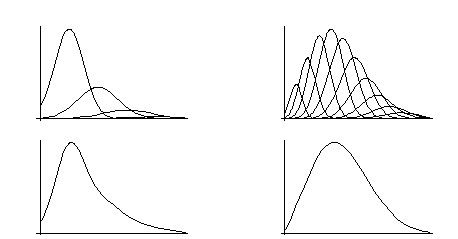
光電子の数が多いとき、Gauss分布に近づくのは当然の要請であるが図でm=1の場合でも離散的な構造が明瞭には見られないかもしれない。
オシロスコープによる直接測定
前の節ではADCとComputerを用いて統計的な測定を行い光電子の個数を決定したが、この節ではオシロスコープで観測されるパルスを元に、全く別の
アプローチができることを示す。
微少光量で観測を続けているうちに例にあげた二つ、三つとパルスが時間的に分離している様子が目につくようになってきた。光量が多いときはそれらのパルス
が重なり合い、個々のパルスの分離は困難であるが、オシロスコープの図形に示したような形をしていればその数を数えることが可能である(もっと高等なオシ
ロスコープで目によらずとも計測が可能であるが、研究者は所有していないので、自らの目を頼りに実験を行った)。この離散的なパルスは、LEDの
DrivePulseが100nsと長いことに起因しており、結果的にこのような別種の測定を可能にした。LEDが発光している間は、いつ光電子が叩き出
されても不思議ではない。現にそのパルスの出現の幅はほぼ100nsの範囲に限定されていたのこの間で時間分解能が充分よければ離散的なパルスが見える
し、これがSingle
Photoelectronであるかどうかテストできる。そこで実際にその数の分布を測定してみることにした。
手法としては非常に原始的ではあるが、直接人間の目によってカウントした。すなわち光量を充分小さくしたフィルターセッティングでLEDが光を出している
100nsの間に光電子増倍管が信号を出した場合、その数を数える。
まずR1332についてフィルタセッティング(ND0.3x14枚、ND0.2x4枚、ND0.1x1枚)の場合とND0.3x13枚、ND0.2x4
枚、ND0.1x1枚)の場合についての信号数分布を示す。
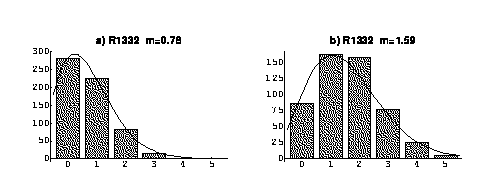
ヒストグラムに現れる実線はポアッソン分布で平均がmの場合である。この図と同じ条件でADCを用いた波高分布は、次のようになる。
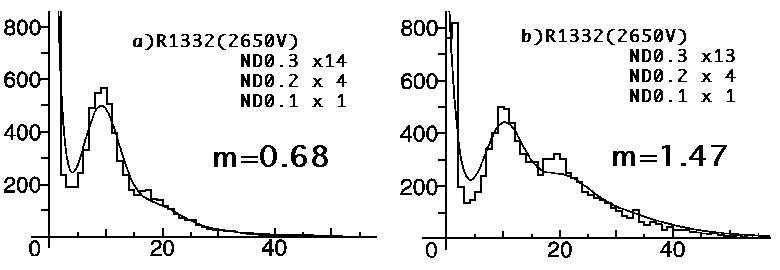
比較すべきデータは・.78と0.68 あるいは、1.59と1.47であり良い一致を示す。すなわち考察した光電子のpoisson分布のかなりの部分
は、この時間的な分布のなかに現われていると思われる。
同様の実験をファインメッシュ型の光電子増倍管に対しても行った。その結果は、次の通りである。
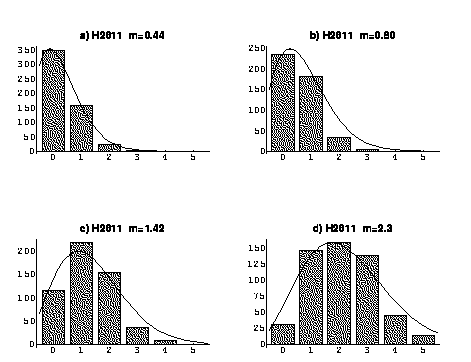
この図の、aはフィルタセッティング(ND0.3x14枚、ND0.2x4枚、ND0.1x1枚)の場合bナあC,c,dとなるにつれてND-filer
0.3の枚数が一枚ずつ減っている(b: ND0.3x13枚、c: ND0.3x12枚、d:
ND0.3x11枚、)。すなわち光量は2倍ずつ変かしている。ポアッソン分布によりフィットされた平均値もおおよそ2倍ずつ変化している。しかしながら
同じ光量でも絶対値はR1332(ラインフォーカス型)の平均値とH2611・ファインメッシュ型)の平均値では約2倍異なる。この原因は、ファインメッ
シュ型のPMTがその構造上各段のメッシュがある程度の透過率を持っており、この透過率はおよそ50%と見積もられているので、約半分の光子にしか信号を
出さない。このため分布が全体としてシフトすると考えられる。すなわち透過率50%をほぼ裏付けたといえよう。またファインメッシュ型のPMTでは入射光
量の増加に対してポアッソン分布によるフィッティングの平均値は直線関係出はない。特に光量が大きくなるとそのずれが大きくなる。これもファインメッシュ
型の光電子増倍管で2段目のメッシュへの透過率がかなり存在し微小信号を作っているため、目視実験ではデータに入らなかった物と考えられる。
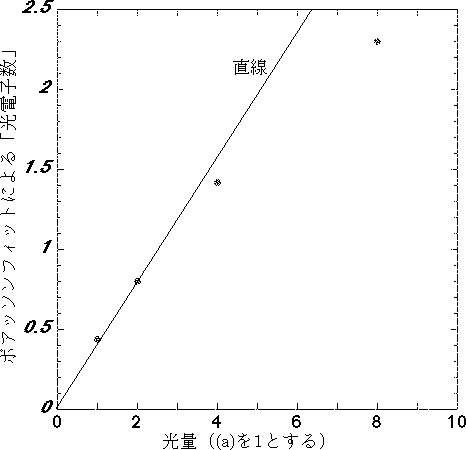
ファインメッシュ型光電子増倍管の微小光量でのテスト
同様の試験を浜松ホトニクス社製ァインメッシュ型光電子増倍管H2611(24)についても実行した。このファインメッシュ型光電子増倍管はN=24とい
う特注の型であり本目的のために増幅率を極限まで高めてある。最大印可電圧は2.7KVでtypical
gainは2.3x10^8である。
ND-filete 0.3 を13枚、0.2を4枚、0.1を1枚で平均光電子数はほぼ1個の場合の光量でのその波高分布を下に示す。
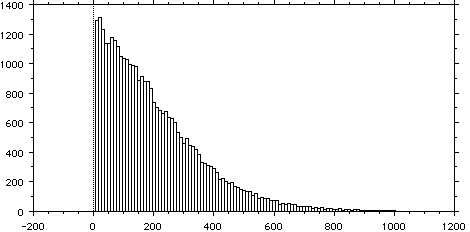
リニアフォーカス型の光電子増倍管と全く異なり、構造は見えない。
またどんなに統計をためて細部を覗いても構造は存在しない。(下図)
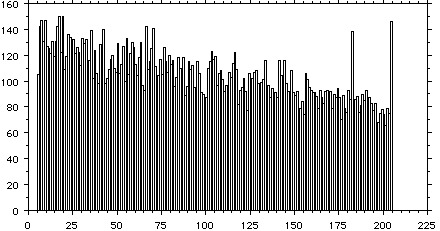
その理由[2]は、リニアフォーカス型の光電子増倍管で行ったシミュレーションは、あくまでもすべてのダイノードにおいて増幅を受ける、という前提があっ
た。しかし、Fine-mesh型のPMTは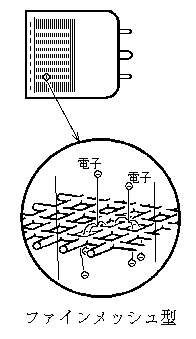 その構造上各段のメッシュがある程度の透過率を持っていなければな
らない。つまり一段目のダイノードで増幅されずに、光電面からいきなり二段目のダイノードに飛び込んでしまう光電子が存在するはずである。この透過率はお
よそ50%と見積もられので、もし24段すべてのメッシュに当たった電子によって微細構造が描かれているのだとしても、一段目に当たらなかったものがほぼ
同数あるのだから、1/dだけ左にシフトした同様の構造によってSingle
Photoelectronのpeekはつぶされてしまう。もちろん、ここで十分な解像度があれば複雑に重なりあった微細構造が見えるのかもしれないが、
少なくともこのPMTのデータから光電子の数を推定することはかなり困難である。この仮定ではdを限りなく1に近づけることができればz前述ののような分
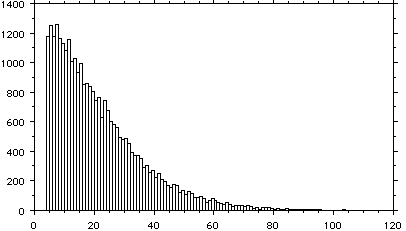
離した山が見えてくるはずである。つまりGainを犠牲にすれば少しでもその構造があらわになると思われる。しかし同じ光量で電圧を下げて見た結果が次の
図であるが、SinglePhotoelectronに対応する山はやはり見ることができなかった。
その構造上各段のメッシュがある程度の透過率を持っていなければな
らない。つまり一段目のダイノードで増幅されずに、光電面からいきなり二段目のダイノードに飛び込んでしまう光電子が存在するはずである。この透過率はお
よそ50%と見積もられので、もし24段すべてのメッシュに当たった電子によって微細構造が描かれているのだとしても、一段目に当たらなかったものがほぼ
同数あるのだから、1/dだけ左にシフトした同様の構造によってSingle
Photoelectronのpeekはつぶされてしまう。もちろん、ここで十分な解像度があれば複雑に重なりあった微細構造が見えるのかもしれないが、
少なくともこのPMTのデータから光電子の数を推定することはかなり困難である。この仮定ではdを限りなく1に近づけることができればz前述ののような分
離した山が見えてくるはずである。つまりGainを犠牲にすれば少しでもその構造があらわになると思われる。しかし同じ光量で電圧を下げて見た結果が次の
図であるが、SinglePhotoelectronに対応する山はやはり見ることができなかった。
まとめ
少なくともラインフォーカス型のPMTでは、信号波高分布と到着時間による信号の分離法の2つの手法のどちらによっても微少光量下の光電子の数を求めるこ
とができた。しかしファインメッシュ型のPMTではパルス波形の解析から個数を求めるには至らなかった。また出力パルスが時間的に離散していることから求
めた値も、絶対値に関して問題がある。これらはひとえに各メッシュの透過率が存在することによるが、メッシュ型の光電子増倍管では透過率が存在しなければ
本質的に光電子増倍管となりえないという問題を抱えているためである。これをどう改善するべきか探る必要がある。



 ここでは、経験則として二
次電子増幅率dの電圧依存性はd=AE^aとして扱う。ここでAは定数、Eはダイノード間電圧、aはダイノードの特性荷よって決まる値で0.7-0.8を
とる。
ここでは、経験則として二
次電子増幅率dの電圧依存性はd=AE^aとして扱う。ここでAは定数、Eはダイノード間電圧、aはダイノードの特性荷よって決まる値で0.7-0.8を
とる。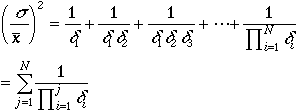



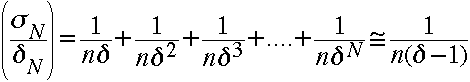
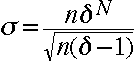
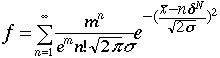







 その構造上各段のメッシュがある程度の透過率を持っていなければな
らない。つまり一段目のダイノードで増幅されずに、光電面からいきなり二段目のダイノードに飛び込んでしまう光電子が存在するはずである。この透過率はお
よそ50%と見積もられので、もし24段すべてのメッシュに当たった電子によって微細構造が描かれているのだとしても、一段目に当たらなかったものがほぼ
同数あるのだから、1/dだけ左にシフトした同様の構造によってSingle
Photoelectronのpeekはつぶされてしまう。もちろん、ここで十分な解像度があれば複雑に重なりあった微細構造が見えるのかもしれないが、
少なくともこのPMTのデータから光電子の数を推定することはかなり困難である。この仮定ではdを限りなく1に近づけることができればz前述ののような分
離した山が見えてくるはずである。つまりGainを犠牲にすれば少しでもその構造があらわになると思われる。しかし同じ光量で電圧を下げて見た結果が次の
図であるが、SinglePhotoelectronに対応する山はやはり見ることができなかった。
その構造上各段のメッシュがある程度の透過率を持っていなければな
らない。つまり一段目のダイノードで増幅されずに、光電面からいきなり二段目のダイノードに飛び込んでしまう光電子が存在するはずである。この透過率はお
よそ50%と見積もられので、もし24段すべてのメッシュに当たった電子によって微細構造が描かれているのだとしても、一段目に当たらなかったものがほぼ
同数あるのだから、1/dだけ左にシフトした同様の構造によってSingle
Photoelectronのpeekはつぶされてしまう。もちろん、ここで十分な解像度があれば複雑に重なりあった微細構造が見えるのかもしれないが、
少なくともこのPMTのデータから光電子の数を推定することはかなり困難である。この仮定ではdを限りなく1に近づけることができればz前述ののような分
離した山が見えてくるはずである。つまりGainを犠牲にすれば少しでもその構造があらわになると思われる。しかし同じ光量で電圧を下げて見た結果が次の
図であるが、SinglePhotoelectronに対応する山はやはり見ることができなかった。