relativity

相対性理論の話し　　　竹下徹（信州大学） mail: tohru@shinshu-u.ac.jp

ここでは相対性理論をかじるとおもしろい（常識と一致しないように見える）事が出てくる話しをします。使うのは中学校程度の算数です。

まず次のことを出発点とします。
「光の進む速さ光速はどの座標系からみても一定である。」
　　座標系とは、ちと耳慣れない言葉ですが、要は誰かがみる時、そこの立ってる所に置いたものさしのことです。ですから光の速さが今地上に居るAさんからみても、またその地上である速さで動いている電車に乗ったBさんからみてもやはり同じであると主張するのです。この意味で光は特別な存在であると言ってます。通常の世界では、地上のAさんからみた電車の中を走る人=Cさんの速さは次のように計算できます。電車の中に座ったBさんがそれを見ています。

(AからみたCの速さ)=(AからみたBの速さ)+(BからみたCの速さ)
ＶCA＝V電車 +VCB
ここでは　　VCAはAからみたCの速さ、V電車はAからみた電車の速さつまりAからみたBの速さ、VCBはBからみたCの速さを表しています。

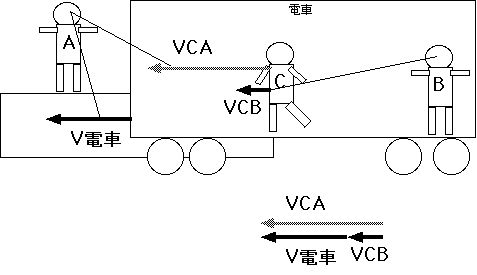
ところが上で述べたことはCが光である場合、この式が通用しないと思えというのです。初めはこんなとてつもないことを誰も信じて議論を始める気にはなれません。でもとにかく信じていただくしかないのです。実際実験を多くの人たちが行いました。その中でも有名なのがマイケルソン・モーレーの実験と呼ばれているものです。地球の自転や公転速度を電車の速さにみたたてて実験しました。そこでは光を２つに分けて、一方を地球の動きと平行に走らせたものともう一方を直角方向（こちらは地球の動きの速さを感じません）に走らせたものを何回か鏡の間だを往復させて戻ってきた光を比べてみたのです。どちらかが早やければちゃんと判るように光の波の動きを監視できるように細工をしてあります。結果は全く一致していました。つまり地球の自転や公転の速度による影響が全くありませんでした。従って
「光りの進む速さ光速はどの座標系からみても一定である。」という一見通常ではあり得ないような事を認めざるを得ません。或いは光は特別なんだと思うほうが納得しやすいかもしれません。

「光りの進む速さ光速はどの座標系からみても一定である。」を認めた上で、やっと相対性理論を始める出発点に立つ事ができました。さてこの電車の中で光を走らせてみます。光速を cと書きます。
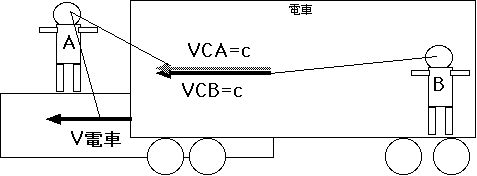
とこういうイメージになります。C さんは今や光に化けてしまっています。さてこの電車の真ん中に光を発するランプとこれをつけたり消したりできるスイッチを取りつけます。さらに電車の前と後ろのかべに鏡を取りつけます。電車の真ん中にいる Cさんがスイッチをいれてランプがつきます。光は前と後ろの壁へ飛んで行き、鏡で反射してCさんの所へ戻ってきます。この右と左からの光のタイミングは正確に同じです。これはCさんにとって同時であると言えます。なにしろ電車のど真ん中にランプがありBさんから鏡までの距離をＬとするとBさんはスイッチをいれてから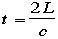秒後に前と後の壁からの光を見るわけです。また Bさんにとっては電車の前後に取りつけられた鏡に光が反射するようすをみるので、鏡に光が到着した時刻は前後で同じだとみるはずです。絵は光が斜めに走ってますが、これは見やすくしたためで、気にしないでください。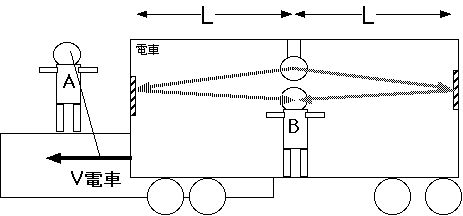
さてこの事件をAさんはどう見るでしょうか？B さんがランプを点灯してからB さんの元へ光がもどるまでに電車が動いているので電車の進行方向へ進む光にとって壁が遠ざかるわけですし、反対に後ろ方向では壁は近づいてきます。つまり Aさんには光の鏡への到着時刻は後ろ側が早く、前が遅いと見えます。このことはB さんのみることとは違います。この事例を一般化すると、同時刻と言う概念は場所が違うときはみる人により異なる。（ある人は同時だといい(Bさん)またある人は同時ではない（Aさん）と言います。これは別に妙なことではありません。さらに一般化して「異なる場所での同時刻は相対的である」ともいいます。ただし2つの同じ場所で同時に起こる事件は Aがみても Bが見ても同じ時間経過後に起こります。

いよいよ相対性理論でおこる奇妙な出来事その１に入ります。それは時間の相対性と呼ばれるものです。いままと同じ状況を考えます。ただし鏡を床に置きます。またまたランプから床までの距離をLとしましょう。
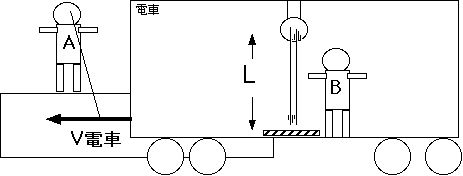
これをみるBさんは光の往復をみてその時間を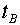を次のようにいいます。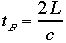あるいは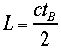と時間を測定したなら距離に関していうことができます。一方Aさんからこの事件をみると次の図のように電車が動いていることを考慮しなくてはいけません。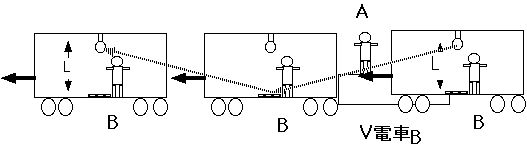
Aさんは光が出た位置と鏡に光が反射する位置と最後に光が再びランプに戻る位置はそれぞれ異なって見えます。Aさんから見た光がランプを出てから再び戻って来るまでの時間を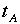とします。さらに光の軌道は二等辺三角形に見えます。その半分は直角三角形で斜辺の長さが光の通った距離で、底辺の長さは（電車の速さ）ｘ（A　さんから見て光がランプを出て鏡につくまでの時間）です。また直角三角形の高さはLです。これは電車の進行方向に直角な方向の長さは　Aさんが見てもBさんが見ても同じになるはずだからです。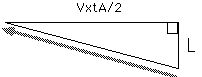ですからこの直角三角形にピタゴラスの定理を使います。ピタゴラスの定理は「直角三角形の斜辺の長さの二乗は直角を挟む二つの辺の長さの二乗の和に等しい」という幾何学の定理です。その証明は自分で考えるか、ちまたにあふれていますので、そちらを見てください。これを使って光の飛んだ距離の二乗が(V x 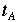/2)²とL²の和に等しいわけですから，式で書くと、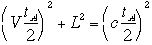、ここで電車の速さをVとします。斜辺の長さは光がランプから出て再びランプに戻るのを見ているAさんの時計の時間　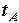の半分にその速度（光速）をかけた物になります。光の速度はどこから見ても一定で cなのでこの式の右辺はcを用いてあります。この式を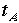について解くことができて、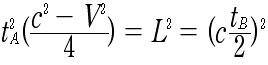という関係式を得ます。これを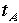=と解くと、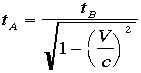となります。この分母の妙な量が相対性理論で良く出るやつです。ちなみにここ至る前に実は c >= Vでないとこの平方根を開くことができません。相対性理論の出発点として「光の進む速さ光速はどの座標系からみても一定である。」を認めてもらってここまで来たのですが、この文は実はさらに光はこの世界で最速であることも要求しています。上の平方根を開くにはこれが無いとできませんね。この世には光の速さを超えて移動する物体はあり得ないのです。それは（ここの話しからずれますが、光の粒子としての性質による物なのです。粒子は全てその質量により区別されます。光の粒子＝光子の質量はゼロです。これより質量の小さい粒子は存在しえませんし、この粒子が最速で動くわけです。（他の質量ゼロの粒子も存在しその速度はやはり光速です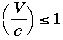））。ですから、平方根のなかはもちろん１より小さい、となると、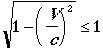ですからその逆数は当然１より大きい。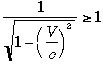ので、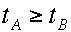となります。これは同じ現象を見ているにもかかわらず、Aの見る時間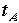がBの見る時間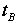に比べてたくさん進むことを示します。逆に言い換えると、Bの見る時間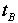はゆっくりすすんだのです。これを「運動する物体B の時間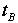は遅れる(少ししか進まない）」ということもあります。どのくらいゆっくり進むかは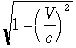これの大きさしだいなのです。我々の普通の世界で実現できる速さVはせいぜい1000km/hでしょう（飛行機の速さ）。これは時速なので、秒速になおしてやりますと、280m/sとなります。１秒間に280m進むっていうと結構速いのですが。光速c= 3x10⁸m/s=300000000m/sに比べると小さなものです。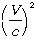をまともに計算してもゼロです。すると問題の量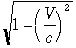は１です。つまり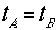が成り立ち我々の通常の世界では運動するものの中に居ると時計がゆっくり進む現象を見ることはできません。

ここにおもしろい昔話があります。浦島太郎物語です。浦島太郎はかめという名の宇宙船に乗って竜宮城へいったそうな。その速度はいったい、いくらだったのでしょうか？浦島太郎が竜宮城で酒池肉林（？）の３年（竜宮城あるいはかめ型ロケットは速度Vで飛んでいたはずだ）を過ごして（浦島時計で３年）帰ってみると郷里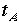では３００年が過ぎていたのだそうな。後で述べる根本的問題を別にして、もしかめ型ロケットあるいは竜宮城が地球に対して速度Vで動き続けていたら（どうやって帰ってきたかが問題なのだが）浦島の時計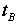はゆっくり進むはずだ。地球の時計で３００年がたつのに浦島時計で３年となる速さVはいくらか？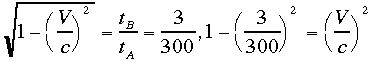
より、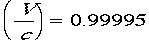なんとかめ号あるいは竜宮城号の速度は光速の0.99995倍、もうほとんど光速で飛ばねばならないのだ！
で本質的問題はどうやってかめ号はぐると回って帰ってきたのかである。つまり相対性理論では一直線に同じ速さで運動をしているときのみ扱うことができて、つまり加速度が無いときである。止まったり回転したりする加速度の働く場合はこの理論では扱いきれないのだ。もっと知りたい人は一般相対性理論を勉強してください。その話はここでの簡単な話の外であるのでこれ以上述べません。その意味でここでの相対性理論は特殊相対性理論と呼ばれます。
浦島伝説はおもしろいがまゆつばとしても、こんなことが実際起こっているのです。それは宇宙線として地上に降り注ぐミュー粒子です。ミュー粒子を止めてその寿命を測定すると t = 2 x 10^-6sです。たとえ光速で進んでも寿命以内に進む距離xは x = ct = 3 x 10⁸x2x10^-6= 600m ただか600ｍです。ミュー粒子が地上30ｋｍの上空で作られるとすると、地上まで生き延びる確率は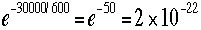と小さく地上でミュー粒子にあえるはずもありません。しかし現実は違います。我々の周りにはミュー粒子が１分当たり1cm²に１個程度降り注いでいます。とするとこれは相対性理論の効果により超高速で運動するミュー粒子の体内時計がゆっくり回っているあいだに地上まで来てしまったと言うことでしょう。例えば10GeVのエネルギーのミュー粒子は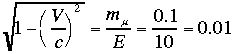　この計算は別の相対性理論の所に詳しく書いてあります。100倍寿命が延びたことに相当し、100倍走ります。平均寿命では600ｍ走ったことを思いだすとその100倍では60km走ることになりゆうゆう地上に到達します。そうです、相対性理論は本当に起こっているのです。我々の世界が（光速に比べて）のろいだけなのです。

「運動する座標系の時計は遅い」というのが相対性理論でおこる奇妙な出来事その1でした。この話は運動は相対的なのでBを止めてというか、とまったBに座標系をくっつけてAを見たらどうなるか？そりゃ　Aの時計がゆっくり進むんだよな。ってことはもしA,B両人が出会うとお互いに矛盾したことになりますね！これがふたごのパラドクスってやつです。自分でもっと調べてみましょう。

さて話しを戻しましょう。
相対性理論でおこる奇妙な出来事その2です。それは長さの相対性と呼ばれるものです。いままでと同じ状況を考えます。ただし鏡を再び電車の前後の壁に置きます。またまたランプから前後の壁の鏡までの距離をBさんが見たらL_B,Aさんが見たらL_A　としましょう。なぜなら運動の進行方向は光の進む方向と直角な方向ではありませんから、AもB同じだとは言い切れません。ですが電車に乗ったBさんには事は簡単で光がランプをでて鏡で往復してランプに帰るまでの時間 t'_Bは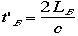です。ダッシュをつけて進行方向の議論をしていることを明白にしておきます。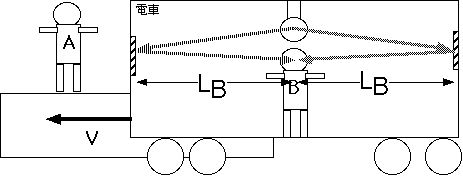さてこれを見る地上のA さんには進行方向（前側）にでた光と反対側（後側）にでた光は異なる見え方をします。まず進行方向（前）へ出た光を考えましょう。鏡が前に進んだ分だけ光は余分に進まなければなりません。Aが見たランプから鏡までの到達時間をt'_A1とすると、次の式が成り立ちます。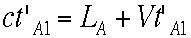従って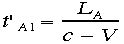となります。更に鏡で反射した光がランプまで戻る時は、距離が短く（進行方向逆向きに光は進み、ランプが向かってきます）なるので、この時間を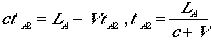　となり、往復時間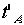は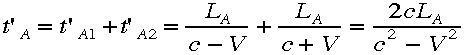となります。さて電車の中央にあるランプからは進行方向とは直角な方向にも光がでて床にも鏡があるとします。床とランプの距離を電車の前後の壁の鏡までの距離と同じにしておきます。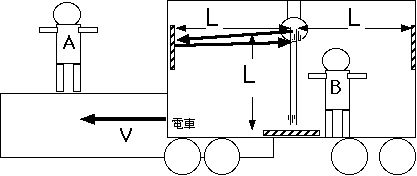
進行方向と直角方向に光に関してBは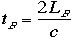といいます。一方Aは、先ほどの議論でだというでしょう。ここでは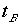の計算結果を代入しました。電車のなかのBにとって電車の進行方向前にでた光がL_Bだけ走ってランプまで戻るのに必要な時間は電車の進行方向とは直角方向で同じL_Bだけ走ってランプまで戻る時間は同じはずであり、二方向から光が戻って来ることは同時刻同じ場所の出来事です。これは電車の外のAが見ても同じ事が起こらなければなりません。つまり 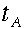= 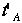のはずです。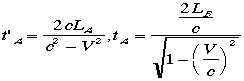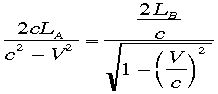。これを解くと、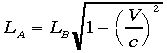となり、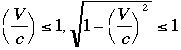を思い出すと、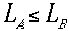であることになります。Aからみると電車の中の長さが短いつまり縮んで見えるのです。「運動する物体ものさしは進行方向に縮む」という表現となります。
またいいますが、現実の世界でこれにお目にかかることはほとんどありません、それは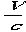がとても小さく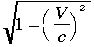はほとんど１に等しいから　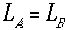で充分なのです。なんで運動するものさしは縮むのかって？そりゃ光速をどんな系からみても一定にしているので、時間が縮めばものさしも縮んで両者のわり算である光速を一定にしているのです。この進行方向に平行な光と直角な光による実験を実際にマイケルソンとモーレーはやってのけたのです。