物理
実験学
竹下徹 (05082002)
確率分布:二項分布
まずは離散分布の代表格の 二項分布を取り上げる。
二項分布とは、n回 試行するとき、r回成功する確率分布である。
ただし、各回の成功確率をpとしこれは一定であるとする。
ということは、例えば3回試行し、1回成功する場合は3とおりあるが、どれも同等と扱って良いことにする。つまり順番の入れ替えは結果の確率には影
響しない、○xx 、x○x、xx○の3つは同じ確率であると考える。
ここで○は成功を表し、x は失敗を表す。4個のコイントス問題も、試行順と考慮し
ないということと、コインを区別しないという事で、同じである。
一般にn回 試行し、r回成功する場合の数は、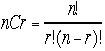 通るある(このときは区別して数える)。またn回中r回成功する確率は、
通るある(このときは区別して数える)。またn回中r回成功する確率は、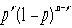 。
よって入れ替えを同等としたn回試行するとき、r回成功する確率は
。
よって入れ替えを同等としたn回試行するとき、r回成功する確率は 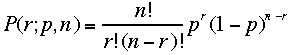 とかける。さて確率であるからには、全確率は1で無ければならな
い。これを示す。すなわち、
とかける。さて確率であるからには、全確率は1で無ければならな
い。これを示す。すなわち、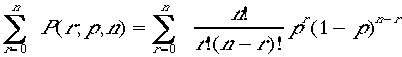
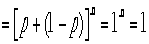 こ
の式は (x+y)のn乗の展開式である。x=p,y=1-p
こ
の式は (x+y)のn乗の展開式である。x=p,y=1-p
では、その期待値<r>は?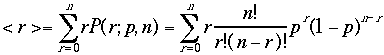 ここでr=0のときは和に寄与しないゼロなので、和をr=1〜n
までとる、さらのnpは定数なので外へ出して、
ここでr=0のときは和に寄与しないゼロなので、和をr=1〜n
までとる、さらのnpは定数なので外へ出して、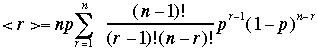 ここでr'=r-1,n'=n-1と置き換える。
ここでr'=r-1,n'=n-1と置き換える。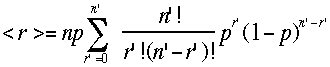 こ
れは全確率の計算と同じだ。つまり、
こ
れは全確率の計算と同じだ。つまり、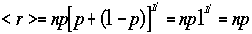 期待値はnpであることが解る。
期待値はnpであることが解る。
離散分布の代表二項分布は、n回試行するとき、r回成功する確率分布である。
ただし、各回の成功確率をpとしこれは一定であるとする。
期待値*<r> =npを計算した。
同様に標準偏差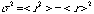 を計算しましょう。トリックは期待値で使ったのと同じのを使います。
を計算しましょう。トリックは期待値で使ったのと同じのを使います。
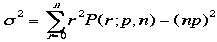
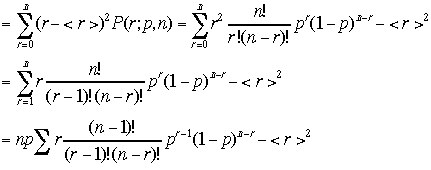
ここで例によって,npを引き出した。さらに置き換えを行う;n'=n-1,r'=r-1,n-r=n'-r'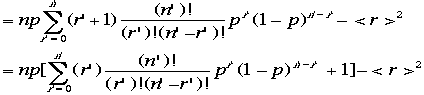
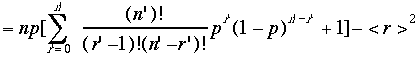 大
かっこの中の[]第2項はいつものもの、のこり第1項をまたトリックを使って計算するとr''=r'-1,n''=n'-1,n'-r'=n''-r''
を使って、
大
かっこの中の[]第2項はいつものもの、のこり第1項をまたトリックを使って計算するとr''=r'-1,n''=n'-1,n'-r'=n''-r''
を使って、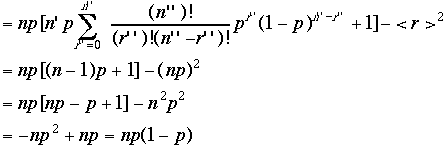 二
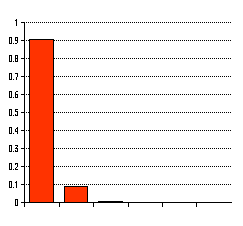
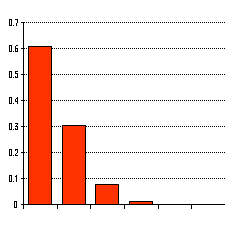
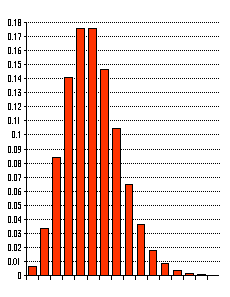
項分布P(r;p,n)の分布のようすを示すグラフを描きましょう。 横軸はr,縦軸は確率P(r;p,n)です。下にその例を示します。
二
項分布P(r;p,n)の分布のようすを示すグラフを描きましょう。 横軸はr,縦軸は確率P(r;p,n)です。下にその例を示します。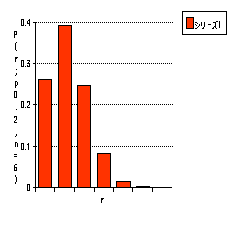
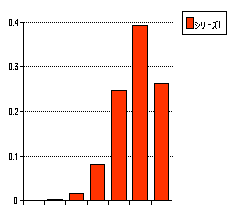 上
はn=6に対する、p=0.2(左)と0.8(右)です。
上
はn=6に対する、p=0.2(左)と0.8(右)です。
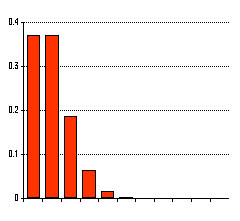
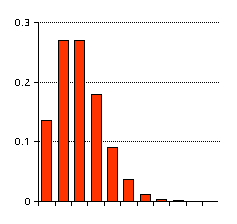
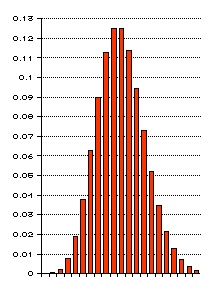
同じようにn=26に対して p=0.2(左)と0.8(右を示します。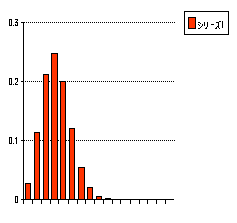
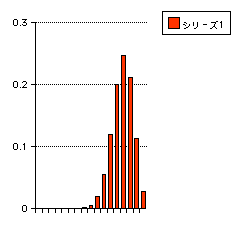 同
じようにn=26に対して p=0.2(左)と0.8(右を示します。
同
じようにn=26に対して p=0.2(左)と0.8(右を示します。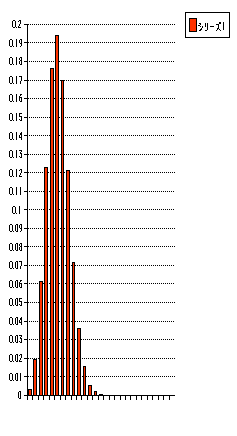
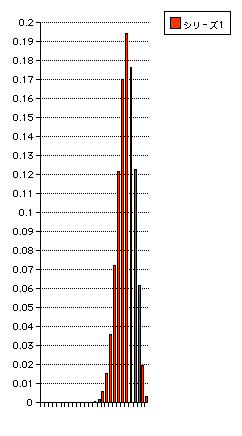
さて二項分布を使う問題です。
(1)
いまヒッチハイクをしようとして道路脇に人が立って車を待ちます。車がヒッチハイカーを拾う確率はどの車も一定で、0.01としましょう。さてこの人が
100台の車が前を通っても、まだ待っている確率はいくらか?
n=100,p=0.01,r=0を計算すると、P(r=0,p=0.01,n=100)=(1-0.01)^100=0.366=0.37
(2)
あるゲームで敵の陣地に爆弾を持ち込んで2個以上爆発させると勝利するとしよう。持ち込むことのできる確率を0.01とすると、何発持ち込めば勝てるか?
ここで何発(n発)持ち込めば(打ち込めば)勝てるか?に対する模範的な答えは、確率いくらで勝てると答えることである。
よって、P(m)をm発持ち込んで爆発させる確率とすると、P(m)は二項分布に従うとして
この戦いに勝利するには、P(m=2), P(m=3),P(m=4),,,,を実現しなくてはいけない。
この無限級数和を取るのは大変なので、全確率は1であることを思い出すと、
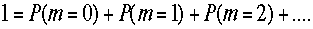 で
あり、m=2以上の和は、P(m=0)とP(m=1)が計算できれば1から引けばよい事が判る。
で
あり、m=2以上の和は、P(m=0)とP(m=1)が計算できれば1から引けばよい事が判る。
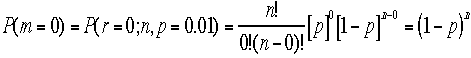
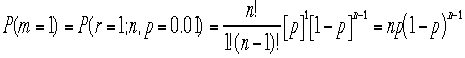
よって勝利の確率は、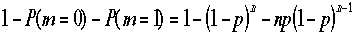
が答えである、しかしこれではいまいち満足できないので、さらに仮定をする。
この確率が0.5よりおおきければ 本当に勝てると。
よって不等式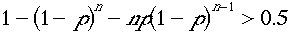 の
解であるnを探せばよい。p=0.01より、
の
解であるnを探せばよい。p=0.01より、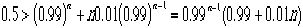
方程式をきれいに解けない!しかし、電卓があるだろう!やみくもにnに値を入れて当たりをつけよう!
ちなみにn=100では、右辺は0.37*(0.99+1)=1.1>0.5であり不適切!
確率分布:ポアソン分布(Poisson)
二項分布は、n回試行するとき、r回成功する確率分布である。ここで各回の成功確率をpとしこれは一定であるとしましたが、ポアソン分
布はこのpが小さい:
p<<1の場合でかつnが不明な場合に相当します。つまり、二項分布でnとpを外から入れてやると、実現回数rの関数として
分布
P(r;n,p)が計算されましたが、ここでは、1個の値を外から入れてやれば良いのです。
この分布をする物理現象としては
p<<1ですあからまれに起こる自然現象があります。例えば、一定時間内に雷のなる回数の分布、(実際雷の放電現象は、雲の
中でn回試行しているのでしょうが、実際雷(放電)に発達する確率は小さいとすれば、使えそうです)、小型の雷として、放射線計測装置の計数の分布(但
し、頻度が低い物)があります。
さて数学的には二項分布において、n->∞を取ります、このときnp=一定に保ったままです。とい
うことは、二項分布ではnp=<r>=λ(iラムダ)で二項分布の期待値ですから、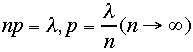 の
極限を二項分布に対して取ります。二項分布の式は、
の
極限を二項分布に対して取ります。二項分布の式は、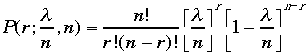 で、n->∞で
で、n->∞で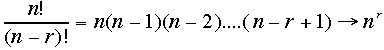
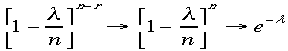 よっ
て
よっ
て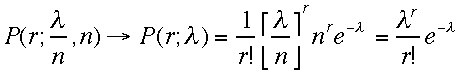 こ
れがポアソン分布と呼ばれるものである。当然、外から入れるのはλのみである。
こ
れがポアソン分布と呼ばれるものである。当然、外から入れるのはλのみである。
このλは期待値になっているはずだ。(あとで計算する)
全確率は、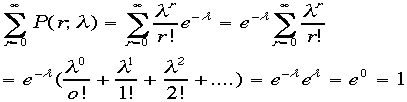
1である事が判り、確率である。ちなみに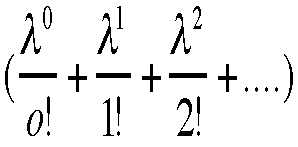 はマクローリン展開
はマクローリン展開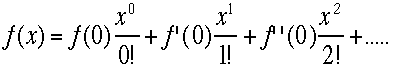 を
使って示すことができる。
を
使って示すことができる。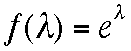 と置くと
と置くと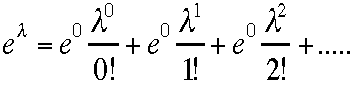 =
=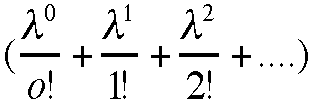 と
なるのでよい。
と
なるのでよい。
離散分布のポアソン分布は、二項分布のある極限で定義した。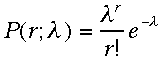 期
待値を計算する;
期
待値を計算する;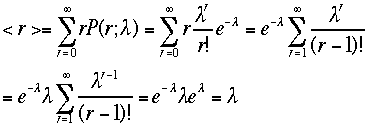 予想通り、<r>=&
lamda;となった。同様の計算により、標準偏差の自乗を計算する、
予想通り、<r>=&
lamda;となった。同様の計算により、標準偏差の自乗を計算する、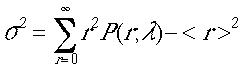 ちょっ
と別の方法でやってみる。
ちょっ
と別の方法でやってみる。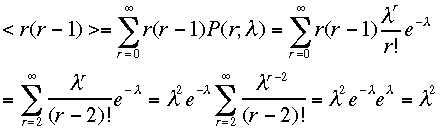
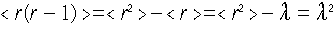 よ
り
よ
り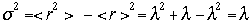 と
なる。
と
なる。
問題(1):二項分布でpが小さい場合というわけで、前回の問題は、全く利用できる。
(1)
いまヒッチハイクをしようとして道路脇に人が立って車を待ちます。車がヒッチハイカーを拾う確率はどの車も一定で、0.01としましょう。さてこの人が
100台の車が前を通っても、と言いたいところだが、nもpも不明であるのがポアソン分布なので、次の様に言い換える;npの積は期待値である。
: (100x0.01=1)の意味づけをする。すなわち1分に平均1台車が通るとして、100分後にまだ待っている確率はいくらか?
問題(2):
あるゲームで敵の陣地に爆弾を持ち込んで2個以上爆発させると勝利するとしよう。持ち込むことのできる確率を0.01とすると、何発持ち込めば勝てるか?
という二項分布の問題をどのように書き換えたらポアソン分布を使う問題になるか?またそれを解け!
ポアソン分布の例をグラフにしよう。
期待値 =0.1.0.5,1.0,2.0,5.0,10.0,20.0,50.
離散分布のポアソン分布は、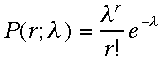 とかかれる。
とかかれる。
ポアソン分布と二項分布はある近似で一致する事の例題です:キーポイント確率・統計より
あなたのクラスのアインシュタインと同じ誕生日の人は何人ですか?
(注意:ここでクラスの人数はかかれていないので、適当に仮定して答えること、また「なんにん」いますかゥ?という問いには何人の確率はいくらと計算する
こと。
二項分布の回答:試行回数nはクラスの人数に対応、50名としよう。二項分布の確率p=誕生日は等確率と考えられるので、p=
1/365で行う。
ちなみに期待値 λ=np=50/365=0.137 人である。
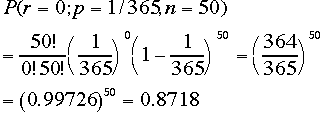 同
様にとなる、
同
様にとなる、
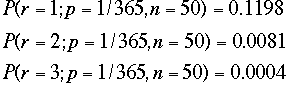 一方これをポアソン分布と考えるなら、
一方これをポアソン分布と考えるなら、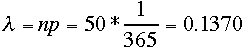 と
して、
と
して、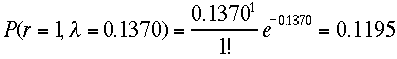 二
項分布では0.1198
二
項分布では0.1198
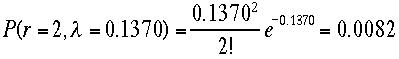 二項分布では0.0081
二項分布では0.0081
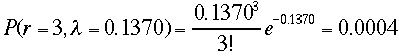 二項分布では0.0004
二項分布では0.0004
と良い近似で両者は近いことが判る。
確率分布:幾何分布
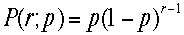 とかかれる分布である。二項分布とはCombinationがな
いところが違う。つまり、順序を意識している。試行を続けてゆき次に成功するまでr回試行するときの確率である事は明らかだ。
とかかれる分布である。二項分布とはCombinationがな
いところが違う。つまり、順序を意識している。試行を続けてゆき次に成功するまでr回試行するときの確率である事は明らかだ。
たとえば、コインのHがでる確率をpとし、Tが出る確率は(1-p)であり、づううと続いてr-1回Tがでる髢セから、その確率は
(1-p)r-1である。これにr回目に確率pでHがでるので、全体の確率はp(1-p)r-1
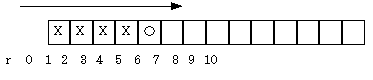 こ
の図では、1回目から4回連続Tが出ているので、(1-p)4そして5回目にHなので、確率pをかける。p(1-p)4。
こ
の図では、1回目から4回連続Tが出ているので、(1-p)4そして5回目にHなので、確率pをかける。p(1-p)4。
確率かどうかは、まず全確率の計算:
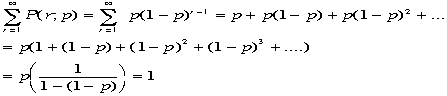
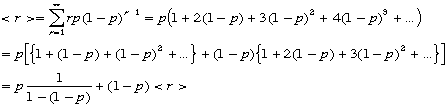
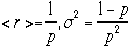 p=
0.1の場合の確率を計算し表を作る。
p=
0.1の場合の確率を計算し表を作る。
 さらにグラフにすると、
さらにグラフにすると、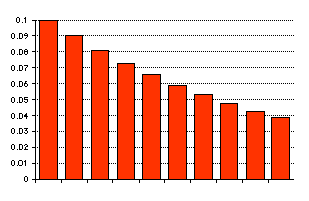 p=
1/6=0.16667の場合のグラフは次のようになる。
p=
1/6=0.16667の場合のグラフは次のようになる。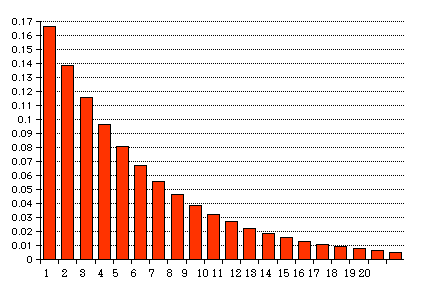
幾何分布の実験
例えば、サイコロを振って、初めて1が出る(2でも3でも良いが)までのサイコロを振る
回数の分布を実験して調べよ。(私はサイコロの代わりに鉛筆を転がした、その結果を示す。
ちなみに半分は我が家の小学生の転がしが入っている)
実線は上のグラフを重ねたもの。幾何分布の例を図に示す:p=1/6=0.16667のサイコロの場合である。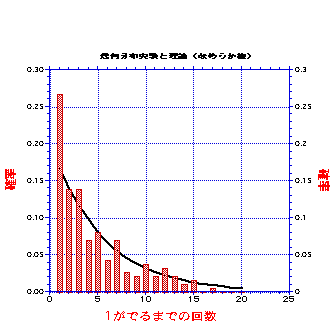
確率分布:指数分布(exponential distribution)
全く偶然に支配される現象がその根底にあるとき、(例えば放射性元素の崩壊事象や、窓口への客の到着時刻)事が起こらない時間間隔0〜
tが存在し、次のある短い時間dtで事が起こる様な現象の確率を考える、これは幾何分布の連続版とも言える物で、幾何分布の説明に使った箱のおもちゃを連
続量として扱うと、時刻t=0からtまで何も起こらず、t〜t+dtで何かが起こる(例えば放射性元素の崩壊事象、あるいは客の窓口への到着)、
この事件全体の確率をP(t)とかこう。
ここで、各箱に対応する短い時間間隔dtのなかで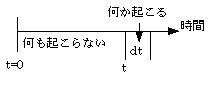
何かが起こる確率は偶然に支配されているので、
一定であるとできる。時刻0からtまでのt分間に
事件(放射性元素の崩壊や客の到来)が起きる数は、ポアソン分布に従うとしてよいので、単位時間あたり平均の事件の起こる数を l
とすると、時間tの間の平均の事件数はlt となる。ここでは、時刻t=0からtまで何もおこらないので、その確率は, 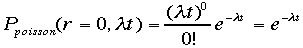 と
かかれる。時刻0からtまでに1個以上の事件の起こる確率は
と
かかれる。時刻0からtまでに1個以上の事件の起こる確率は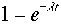 で
あり、
で
あり、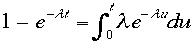 と
いう関係式があるので、連続分布の確率は、確率密度関数から積分して導かれることを思い出すと、この式は、時刻0からtまでに1個以上の事件の起こる確率
密度関数 P^(u)が
と
いう関係式があるので、連続分布の確率は、確率密度関数から積分して導かれることを思い出すと、この式は、時刻0からtまでに1個以上の事件の起こる確率
密度関数 P^(u)が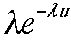 であることを示している。ただし、u>0の条件付き
であるし、また確率密度関数 P^(u)=0,
u<0である。 この分布は確率密度関数がexponetial(指数型)なので指数分布と呼ばれる。まとめると、確率密度関数
であることを示している。ただし、u>0の条件付き
であるし、また確率密度関数 P^(u)=0,
u<0である。 この分布は確率密度関数がexponetial(指数型)なので指数分布と呼ばれる。まとめると、確率密度関数 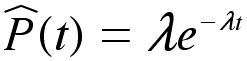 は
時刻t〜t+dtの間にで何かが起こる確率密度であり、その積分である
は
時刻t〜t+dtの間にで何かが起こる確率密度であり、その積分である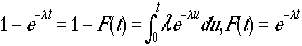 は
時刻t=0〜tまでの間に何かが起こる確率である。よって(1-F(t))でかかれた
F(t)は時刻t=0〜tの間なにも起こらず、t〜t+dtの間に何かが起こる確率の積となっている。
は
時刻t=0〜tまでの間に何かが起こる確率である。よって(1-F(t))でかかれた
F(t)は時刻t=0〜tの間なにも起こらず、t〜t+dtの間に何かが起こる確率の積となっている。
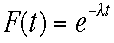 こ
れが指数分布である。
こ
れが指数分布である。
問題: ある電気製品の故障するまでの時間の期待値は2年であるという.この製品が多数販売されているとき,1
年以内に故障する製品の割合はいくらか.
時刻t =
0の時点で正常なy0個の製品があって,時間の経過にしたがって,それぞれが独立に一定の確率で故障するとする(放射性同位元素と同じだ)。さて,ある時
刻tで正常な製品の数をy(t)個として、時刻t
からt +dtの間の微少時間dtの間に故障する製品の数(dy)の「y(t)に対する割合」は,独立に一定の確率で故障するので,t
によらず一定である.したがって,その割合をλであらわすと,次の微分方程式が成り立つ。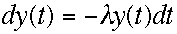 こ
れを解くと、
こ
れを解くと、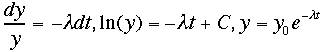 この微分方程式の解は,初期値y0のときy(t) =
y0e-λtとなります.ここで,(y0
- y(t)) / y0という量は「時刻
0からtの間に故障した製品の数の,最初にあった製品の数に対する割合」を示しています.それぞれの製品は独立に故障しますから,この量は「1つの製品
この微分方程式の解は,初期値y0のときy(t) =
y0e-λtとなります.ここで,(y0
- y(t)) / y0という量は「時刻
0からtの間に故障した製品の数の,最初にあった製品の数に対する割合」を示しています.それぞれの製品は独立に故障しますから,この量は「1つの製品
が時刻
0からtの間に故障する確率」と考えることができます.そこで,確率変数Xを「1つの製品が故障するまでの時間(すなわち寿命)」とすると,(y0
- y) / y0は「1つの製品が故障するまでの時間がt以下である確率」すなわちP(X<=t)と同じです.つまり 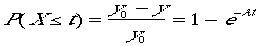 こ
れをtで微分すると確率密度関数f(t)が次のように得られます.
こ
れをtで微分すると確率密度関数f(t)が次のように得られます.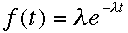 ただし,これはt>=0のときだけで,t
< 0のときはf(t)=
0とします.この確率分布を指数分布といい,これまでの導出過程でわかるように,指数分布は前回説明した幾何分布に対応する,連続的待ち時間分布になりま
す.図は指数分布の確率密度関数のグラフです.「小さい値ほど出やすい」ことがわかります.
図.指数分布の確率密度関数
ただし,これはt>=0のときだけで,t
< 0のときはf(t)=
0とします.この確率分布を指数分布といい,これまでの導出過程でわかるように,指数分布は前回説明した幾何分布に対応する,連続的待ち時間分布になりま
す.図は指数分布の確率密度関数のグラフです.「小さい値ほど出やすい」ことがわかります.
図.指数分布の確率密度関数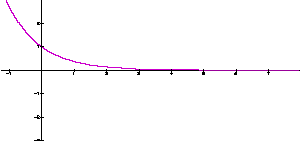
指数分布(確率密度関数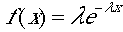 がこのようにかかれる時)の全確率、期待値と分散s2を計算しよ
う。連続分布の期待値や分散は確率密度関数の積分で表されるので、全確率は
がこのようにかかれる時)の全確率、期待値と分散s2を計算しよ
う。連続分布の期待値や分散は確率密度関数の積分で表されるので、全確率は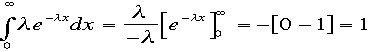 期
待値は
期
待値は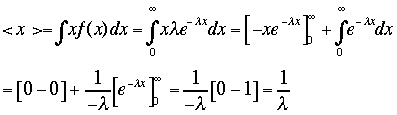 分
散は
分
散は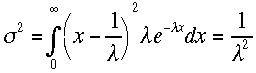 と
なる。
と
なる。
さて窓口や放射性元素のようにどのタイミングで窓口の客が来るか、あるいは崩壊するかはランダムであるという。つまり、どのタイミングかは判らないことを
ランダムという。これを電卓の乱数(RND)を使って遊んでみよう。rndキーを押すと0から1の間の乱数(ランダムなネ数値)が表示される、何度かやっ
てみると、毎回違うようだ。
(1)ランダムかどうか調べよ。ヒント:ランダムということは、微少区間では確率は一定である。
(2)複数の乱数を大小順に並べてそれらの差の絶対値はどういう分布をするか、試せ!これが窓口で待つ銀行員(ある驍「は放射性同位元素の崩壊現象の寿命
を測定する実験)の待ち時間分布であることは、判ってもらえるかな?
窓口や放射性元素のようにどのタイミングで窓口の客が来るか、あるいは崩壊するかはランダムであるという。どのタイミングかは判らない
ことをランダムという。これを電卓の乱数(random
number)を使って遊んでみよう。RAN#キーを押すと0から1の間の乱数
(実数のランダムな数値)が表示される、何度かやってみると、毎回違うようだ。
(1)ランダムかどうか調べよ。ヒント:ランダムということは、微少区間では確率は一定であ ランダムか?
乱数100個を並べる: 0.513886 0.175747 0.308661 0.534550 0.947657 0.171742
0.702253 0.226438 0.494789 0.124724 0.083901 0.389659 0.277234
0.368082 0.98
3467 0.535414 0.765705 0.646493 0.767162 0.780261 0.822977 0.151937
0.625496 0.314694 0.346912 0.917232 0.519776 0.401166 0.606777 0.785426
0.931551 0.869948 0.866551 0.674541 0.758423 0.581911 0.389260
0.355646 0.200238 0.826952 0.415916 0.463536 0.979193 0.126440
0.212643 0.958481 0.737485 0.409069 0.780137 0.757922 0.956871
0.028097 0.318737 0.756957 0.243002 0.589560 0.043426 0.956054
0.319143 0.059362 0.441890 0.915048 0.572265 0.118842 0.569788
0.252056 0.495873 0.236741 0.476975 0.406106 0.873024 0.426976
0.358229 0.381999 0.043181 0.160592 0.522367 0.696602 0.097103
0.400859 0.773455 0.244834 0.342835 0.230001 0.297886 0.304555
0.887234 0.036671 0.651167 0.398619 0.676318 0.732601 0.937825
0.233287 0.838507 0.967239 0.778662 0.431531 0.674123 0.809383
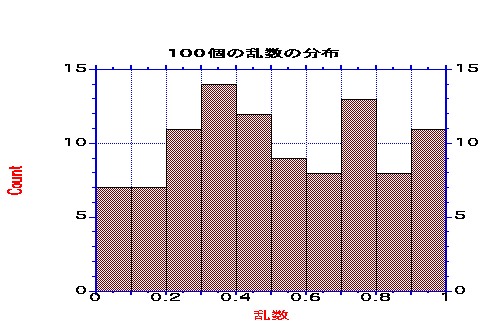
る。これを一様分布という。乱数100個を並べると上の図のようにまだバラバラしている、乱数の数がたらないようだ。
そこで乱数100万個で実行:っとこのくらい平ら(ランダム)になりました。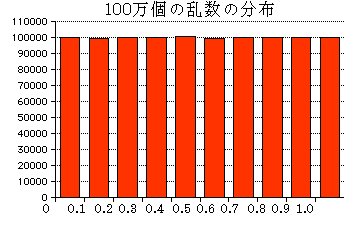 こ
こで縦軸のサイズが大きくなった事が判りますね。そして相対的に変動が小さくなった事も判るでしょう。
こ
こで縦軸のサイズが大きくなった事が判りますね。そして相対的に変動が小さくなった事も判るでしょう。
とても人手でできる範囲を超えています。当然ですが、computerを使いました。どうやってやったかは、私の別の授業(計算物理:対象2年生)を試し
てください。
(2)次に二つの乱数の間の差の絶対値はどういう分布をするか、試せ!これが窓口で待つ銀行員(あるいは放射性同位元素の崩壊現象の寿命を測定する実験、
あるいはあなたのバス停への到着がランダムとしたバス)の待ち時間分布であることは、判ってもらえるかな?体験と違いますか?実は、銀行の窓口に現れる人
のタイミングを乱数を振ることによりシミュレーションをしましたが、銀行の窓口の人の待ち時間は、すべての人のタイミングを決めた後、
つまり、適当な個数の乱数を振って(これにより、人が窓口に到着するタイミングを決める)、これを時刻とみなし順番に並べ(例えば大きい順に)、そのそれ
ぞれのとなりあう二つのタイミングの差の分布をといるべきでした。
そこで、上で述べたことをやってみます。100個の乱数を作り、大きい順に並べ替えます。そして隣り合う値の差を抜き出し、その分布をヒストグラムにしま
す。
0.028097 0.036671 0.043181 0.043426 0.059362 0.083901 0.097103
0.118842 0.124724
0.126440 0.151937 0.160592 0.171742 0.175747 0.200238 0.212643
0.226438 0.230001 0.233287 0.236741 0.243002 0.244834 0.252056
0.277234 0.297886 0.304555 0.308661 0.314694 0.318737 0.319143
0.342835 0.346912 0.355646 0.358229 0.368082 0.381999 0.389260
0.389659 0.398619 0.400859 0.401166 0.406106 0.409069 0.415916
0.426976 0.431531 0.441890 0.463536 0.476975 0.494789 0.495873
0.513886 0.519776 0.522367 0.534550 0.535414 0.569788 0.572265
0.581911 0.589560 0.606777 0.625496 0.646493 0.651167 0.674123
0.674541 0.676318 0.696602 0.702253 0.732601 0.737485 0.756957
0.757922 0.758423 0.765705 0.767162 0.773455 0.778662 0.780137
0.7802610.785426 0.809383 0.822977 0.826952 0.838507 0.866551
0.869948 0.873024 0.887234
0.915048 0.917232 0.931551 0.937825 0.947657 0.956054 0.956871
0.958481 0.96723
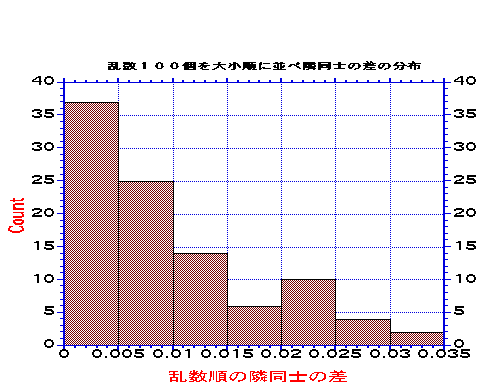
右下がりの分布ですが、なに分布なのかは判断つきません。縦軸をlogで再plotしてみる。100個では不足のようだがまだ、先ほどのグラフよりまし。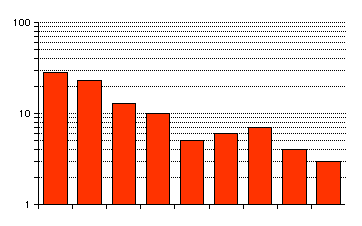
では大数の法則に従えば理想的な指数関数分布に近づくのか試してみよう。1万個の乱数を発生させて(もちろん計算機で)それを大小順に
並べおのおのの差を取り、その差のヒストグラムを上記の100個の場合のように取ってみた。次の図である。始めは縦軸が通常の個数(頻度)である。横軸は
差の広がりを20個のビンに分けた。次の図は縦軸のlogを取った。指数関数なら直線に見えるだろう。
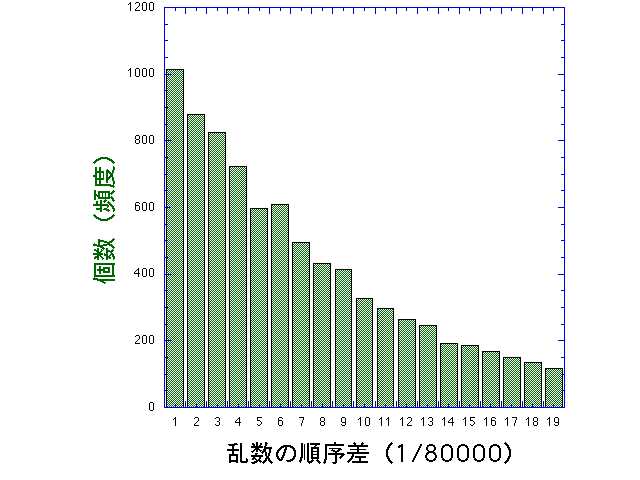
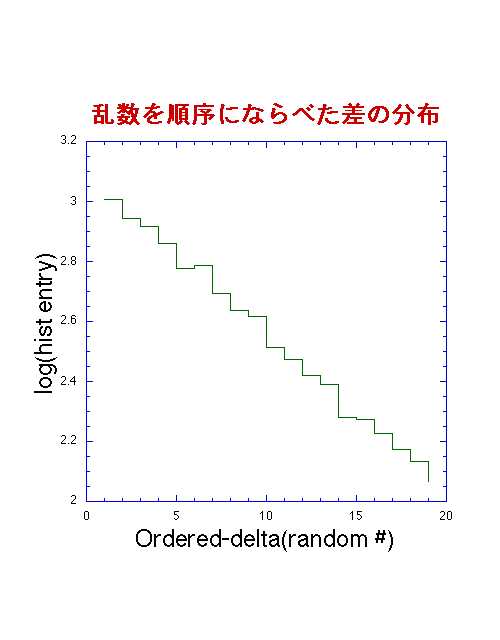
確率分布:ガウス分布
連続分布:ガウス分布(正規分布とよばれることもある)
これは二項分布やポアソン分布の離散分布を連続化したものである。
(幾何分布を連続化して指数分布を得た)
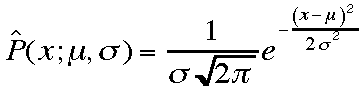 とかかれる確率密度関数である。パラメーターは2つ、μとσであ
る。また変数xは連続変化する量である。下のグラフはガウス関数です。高さの値はm=0,s=5の時の計算値です。
とかかれる確率密度関数である。パラメーターは2つ、μとσであ
る。また変数xは連続変化する量である。下のグラフはガウス関数です。高さの値はm=0,s=5の時の計算値です。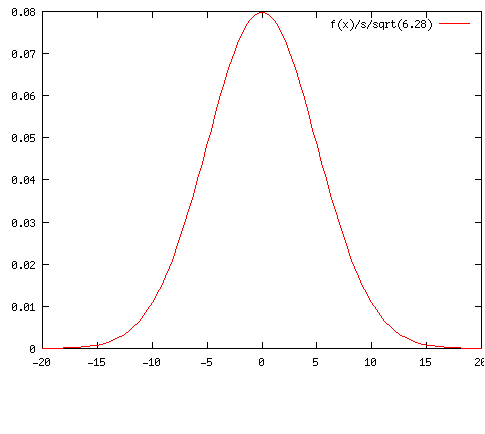 連
続分布:ガウス分布(正規分布とよばれることもある)
連
続分布:ガウス分布(正規分布とよばれることもある)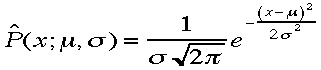 が確率密度関数であることを示そう。(1)全確率は
が確率密度関数であることを示そう。(1)全確率は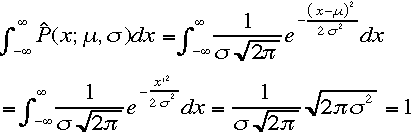 こ
こで公式
こ
こで公式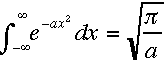 を
使った。
を
使った。
同様に xの期待値<x>は
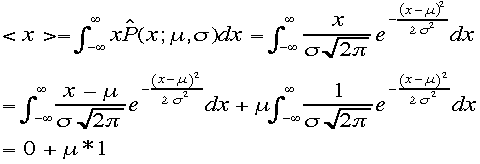 よ
り、
よ
り、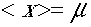 ,
となる。ここで
,
となる。ここで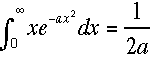 となる。また分散
となる。また分散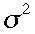 は
は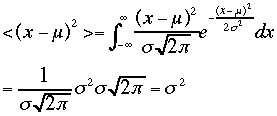 で
あることが解る、だからずううと分散にシグマの二乗を使ってきた。ただし
で
あることが解る、だからずううと分散にシグマの二乗を使ってきた。ただし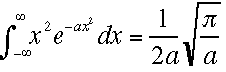 であることを使った。
であることを使った。
連続分布:ガウス分布は確率密度関数であるから、実際に役立つ確率にするには積分する必要がある。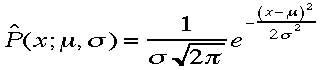 が
確率密度関数である。このため、積分を計算することはでき無くないが、便利のために積分表が作られている。しかし、 期待値と分散についてその都度表を作
ることは無駄なので、変数変換を行い統一化した表が用いられる。そこでの変数はz一つである。
が
確率密度関数である。このため、積分を計算することはでき無くないが、便利のために積分表が作られている。しかし、 期待値と分散についてその都度表を作
ることは無駄なので、変数変換を行い統一化した表が用いられる。そこでの変数はz一つである。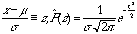 積
分には2種類が一般に用意されている。x=mの周りに対称に積分した表(two
tailed)と、-∞からx=bまで積分した表(one tailed)である。表参照
積
分には2種類が一般に用意されている。x=mの周りに対称に積分した表(two
tailed)と、-∞からx=bまで積分した表(one tailed)である。表参照
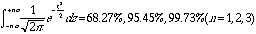 この意味は、n=1なら分布がガウス分布に従うとして、平均が
m,分散がs2が判っていて測定値のXがm-1sからm+1sの間に来る確率は68.27%である事を意味する。
この意味は、n=1なら分布がガウス分布に従うとして、平均が
m,分散がs2が判っていて測定値のXがm-1sからm+1sの間に来る確率は68.27%である事を意味する。
表から自分で次の事を確かめてください。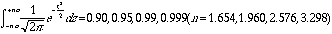 同様にn=1.645のときは、分布がガウス分布に従うとして、
平均がm,分散がsが判っていて測定値のXがm+1sより小さい確率は90%である事を意味する。
同様にn=1.645のときは、分布がガウス分布に従うとして、
平均がm,分散がsが判っていて測定値のXがm+1sより小さい確率は90%である事を意味する。
-∞からx=bまで積分した表(one tailed)である表は、実際はtwo-tailedの表から計算可能である。
ポアソン分布の
グラフを描いて判ったと思うが、ポアソン分布で期待値lが大きいときはグラフはガウス分布に近づく。ポアソン分布のグラフで期待値lが小さいときは左の片
のおちかたは急で左右非対称であるが、期待値lが大きくなると左右対称に近づく。
数学的にポアソン分布の式をStarlingの公式を用いてガウス関数に持って行く事ができる。ここではそれは行わない。各自調べておいてほしい。
問題:期待値5.7のポアソン分布に従う分布があるとしよう。
(1)2以下事が起こる確率を計算せよ。
(2)これをガウス分布すると強引に考えるとき、その確率を求めよ。ただし、ガウス分布ではxは実数であるので、2回以下とは、x<2.5
のことである。
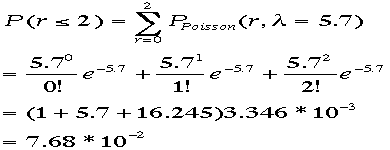
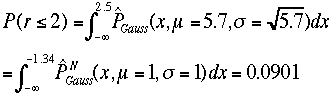 充分大きな期待値ではないが、7.5%(ポアソン分布)と9%
(ガウス分布)は近い!ポアソン分布とガウス分布は親戚だ。
充分大きな期待値ではないが、7.5%(ポアソン分布)と9%
(ガウス分布)は近い!ポアソン分布とガウス分布は親戚だ。
2者択一の40問中60%正解すると合格する試験がある、これにサルが挑む。サルが合格する確率を二項分布の場合、とガウス分布の場合
で計算せよ。
ここでサルとは2者択一でランダムに応える回答者を代表している。
二項分布: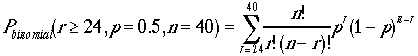 =0.134
である。
=0.134
である。
一方ガウス分布を仮定すると、
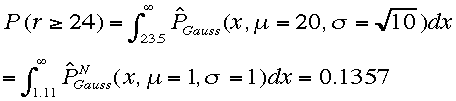 と
なる。つまり、両者は近い。二項分布とガウス分布も親戚だ。
と
なる。つまり、両者は近い。二項分布とガウス分布も親戚だ。
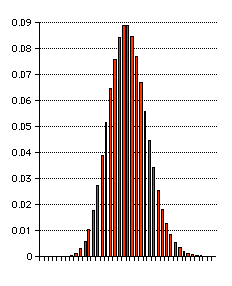
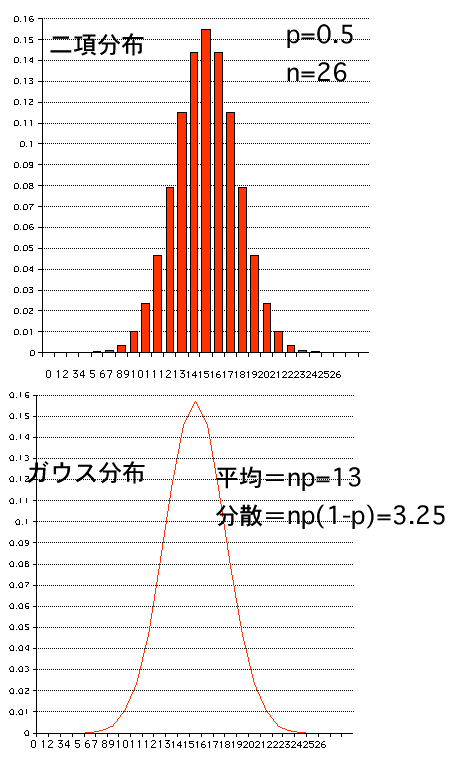
これをヒストグラムで示してみよう。二項分布とガウス分布を比較する、平均値あるいは期待値を13とする様に二項分布では n=26,
p=0.5 を選んだ。またガウス分布で
は 平均=13、分散=n*p*(1-p)=3.25を選んでプロットした。
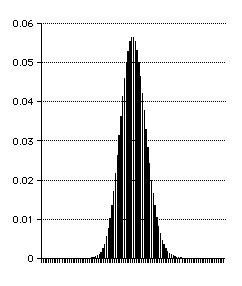
同様にポアソン分布とガウス分布を比較する、平均値あるいは期待値を13とする様に
ポアソン分布では 北市=13 を選んだ。またガウス分布で
は 平均=13、分散=sqrt(期待値)=3.6を選んでプロットした。
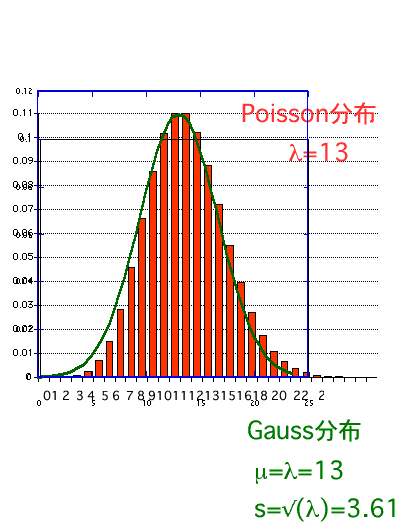
ポアソン分布は本来横軸が無限大までつづく分布なので、右へ長い尾を引く。これが左右完全に対象なガウス分布とは少々異なる形であることが見て取れる。
おまけ:
ポアソン分布から数学的にガウス分布を導出する。
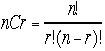 通るある(このときは区別して数える)。またn回中r回成功する確率は、
通るある(このときは区別して数える)。またn回中r回成功する確率は、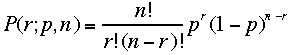 とかける。さて確率であるからには、全確率は1で無ければならな
い。これを示す。すなわち、
とかける。さて確率であるからには、全確率は1で無ければならな
い。これを示す。すなわち、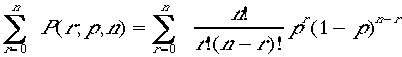
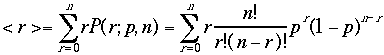 ここでr=0のときは和に寄与しないゼロなので、和をr=1〜n
までとる、さらのnpは定数なので外へ出して、
ここでr=0のときは和に寄与しないゼロなので、和をr=1〜n
までとる、さらのnpは定数なので外へ出して、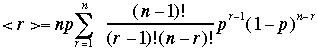 ここでr'=r-1,n'=n-1と置き換える。
ここでr'=r-1,n'=n-1と置き換える。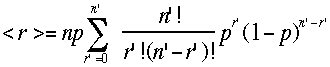 こ
れは全確率の計算と同じだ。つまり、
こ
れは全確率の計算と同じだ。つまり、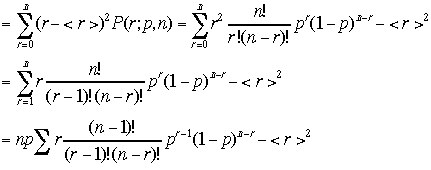
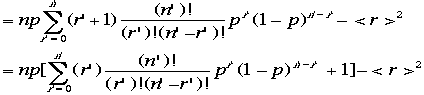
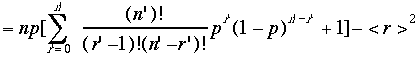 大
かっこの中の[]第2項はいつものもの、のこり第1項をまたトリックを使って計算するとr''=r'-1,n''=n'-1,n'-r'=n''-r''
を使って、
大
かっこの中の[]第2項はいつものもの、のこり第1項をまたトリックを使って計算するとr''=r'-1,n''=n'-1,n'-r'=n''-r''
を使って、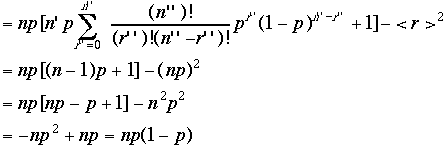 二
項分布P(r;p,n)の分布のようすを示すグラフを描きましょう。 横軸はr,縦軸は確率P(r;p,n)です。下にその例を示します。
二
項分布P(r;p,n)の分布のようすを示すグラフを描きましょう。 横軸はr,縦軸は確率P(r;p,n)です。下にその例を示します。
 上
はn=6に対する、p=0.2(左)と0.8(右)です。
上
はn=6に対する、p=0.2(左)と0.8(右)です。
 同
じようにn=26に対して p=0.2(左)と0.8(右を示します。
同
じようにn=26に対して p=0.2(左)と0.8(右を示します。

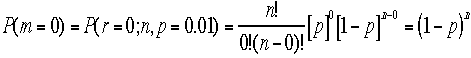
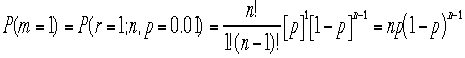
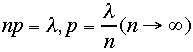 の
極限を二項分布に対して取ります。二項分布の式は、
の
極限を二項分布に対して取ります。二項分布の式は、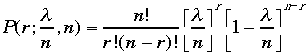 で、n->∞で
で、n->∞で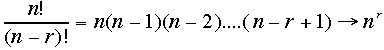
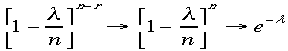 よっ
て
よっ
て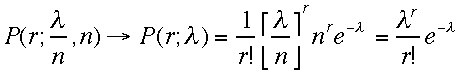 こ
れがポアソン分布と呼ばれるものである。当然、外から入れるのはλのみである。
こ
れがポアソン分布と呼ばれるものである。当然、外から入れるのはλのみである。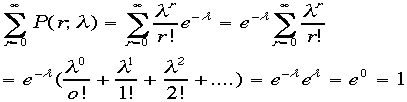
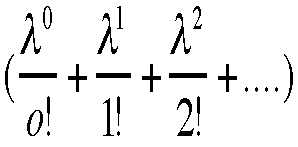 はマクローリン展開
はマクローリン展開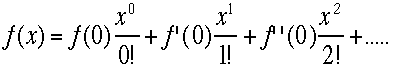 を
使って示すことができる。
を
使って示すことができる。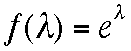 と置くと
と置くと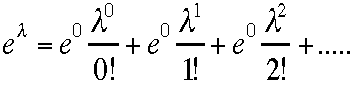 =
=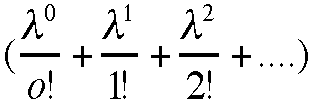 と
なるのでよい。
と
なるのでよい。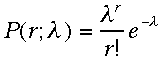 期
待値を計算する;
期
待値を計算する;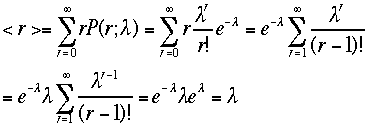 予想通り、<r>=&
lamda;となった。同様の計算により、標準偏差の自乗を計算する、
予想通り、<r>=&
lamda;となった。同様の計算により、標準偏差の自乗を計算する、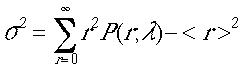 ちょっ
と別の方法でやってみる。
ちょっ
と別の方法でやってみる。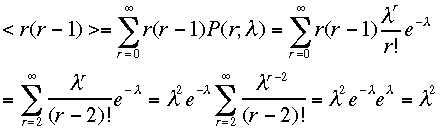








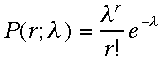 とかかれる。
とかかれる。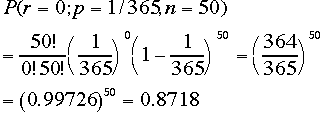 同
様にとなる、
同
様にとなる、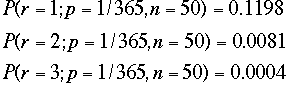 一方これをポアソン分布と考えるなら、
一方これをポアソン分布と考えるなら、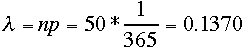 と
して、
と
して、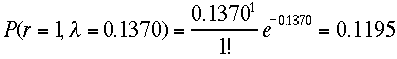 二
項分布では0.1198
二
項分布では0.1198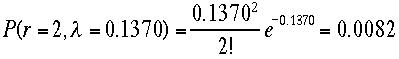 二項分布では0.0081
二項分布では0.0081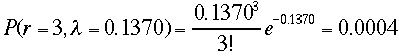 二項分布では0.0004
二項分布では0.0004 こ
の図では、1回目から4回連続Tが出ているので、(1-p)4そして5回目にHなので、確率pをかける。p(1-p)4。
こ
の図では、1回目から4回連続Tが出ているので、(1-p)4そして5回目にHなので、確率pをかける。p(1-p)4。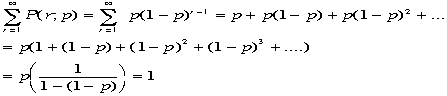
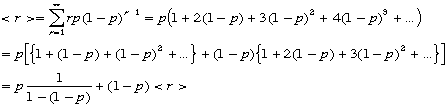
 さらにグラフにすると、
さらにグラフにすると、 p=
1/6=0.16667の場合のグラフは次のようになる。
p=
1/6=0.16667の場合のグラフは次のようになる。


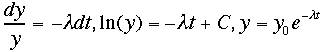 この微分方程式の解は,初期値y0のときy(t) =
y0e-λtとなります.ここで,(y0
- y(t)) / y0という量は「時刻
0からtの間に故障した製品の数の,最初にあった製品の数に対する割合」を示しています.それぞれの製品は独立に故障しますから,この量は「1つの製品
この微分方程式の解は,初期値y0のときy(t) =
y0e-λtとなります.ここで,(y0
- y(t)) / y0という量は「時刻
0からtの間に故障した製品の数の,最初にあった製品の数に対する割合」を示しています.それぞれの製品は独立に故障しますから,この量は「1つの製品
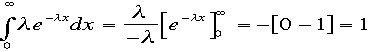 期
待値は
期
待値は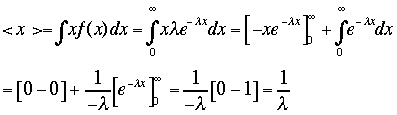 分
散は
分
散は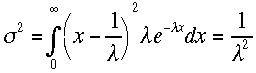 と
なる。
と
なる。
 こ
こで縦軸のサイズが大きくなった事が判りますね。そして相対的に変動が小さくなった事も判るでしょう。
こ
こで縦軸のサイズが大きくなった事が判りますね。そして相対的に変動が小さくなった事も判るでしょう。



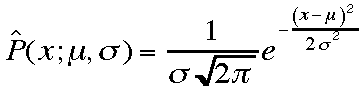 とかかれる確率密度関数である。パラメーターは2つ、μとσであ
る。また変数xは連続変化する量である。下のグラフはガウス関数です。高さの値はm=0,s=5の時の計算値です。
とかかれる確率密度関数である。パラメーターは2つ、μとσであ
る。また変数xは連続変化する量である。下のグラフはガウス関数です。高さの値はm=0,s=5の時の計算値です。 連
続分布:ガウス分布(正規分布とよばれることもある)
連
続分布:ガウス分布(正規分布とよばれることもある)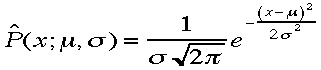 が確率密度関数であることを示そう。(1)全確率は
が確率密度関数であることを示そう。(1)全確率は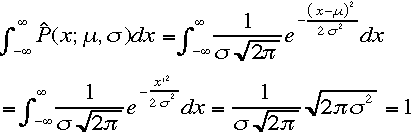 こ
こで公式
こ
こで公式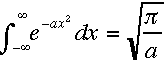 を
使った。
を
使った。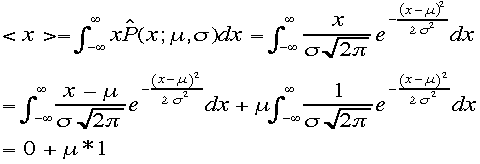 よ
り、
よ
り、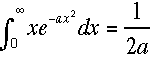 となる。また分散
となる。また分散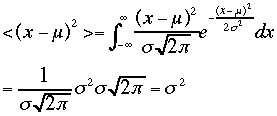 で
あることが解る、だからずううと分散にシグマの二乗を使ってきた。ただし
で
あることが解る、だからずううと分散にシグマの二乗を使ってきた。ただし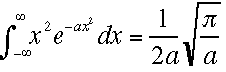 であることを使った。
であることを使った。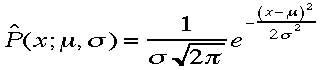 が
確率密度関数である。このため、積分を計算することはでき無くないが、便利のために積分表が作られている。しかし、 期待値と分散についてその都度表を作
ることは無駄なので、変数変換を行い統一化した表が用いられる。そこでの変数はz一つである。
が
確率密度関数である。このため、積分を計算することはでき無くないが、便利のために積分表が作られている。しかし、 期待値と分散についてその都度表を作
ることは無駄なので、変数変換を行い統一化した表が用いられる。そこでの変数はz一つである。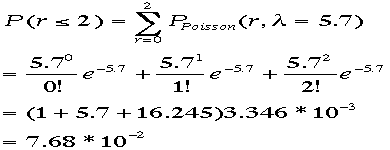
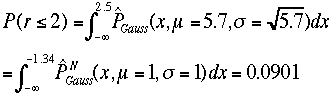 充分大きな期待値ではないが、7.5%(ポアソン分布)と9%
(ガウス分布)は近い!ポアソン分布とガウス分布は親戚だ。
充分大きな期待値ではないが、7.5%(ポアソン分布)と9%
(ガウス分布)は近い!ポアソン分布とガウス分布は親戚だ。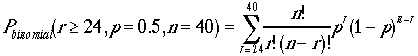 =0.134
である。
=0.134
である。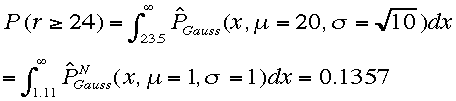 と
なる。つまり、両者は近い。二項分布とガウス分布も親戚だ。
と
なる。つまり、両者は近い。二項分布とガウス分布も親戚だ。
