すなわち、精度の良い実験では
物理実験学 (5)
竹下徹 (04June2002)
精度の伝搬(誤差の伝搬ともいう人もいる):
種々の測定値があるとき、どうやってまとめるか考えよう。
精度の評価が異なる2つの実験結果をどうやって組み合わせるべきか?
例:2つの電圧計があって、同じ電圧を測ったとしよう。
電圧計Aの最小メモリは1V,電圧計Bの最小メモリは0.1V,
電圧計Aの読みVAと電圧計Bの読みVBの両方を知ってあなたはどういう結論をくだすか?
アイデfア1 電圧計Aの精度は悪いので、そのデータを無視する。
アイデア2 電圧計Aの読みと電圧計Bの読みの平均値を取る。
アイデア3:アイデア1とアイデア2を含むやり方、重みを定義する。
WAとWBとしよう、2つの電圧計で測った2つの測定の総合結果として、
V=(WA*VA+WB*VB)/(WA+WB) として電圧を得る。
アイデア1はWA=0.0,WB=1.0に相当する、アイデア2はWA=0.5,WB=0.5ということ。
どうやって WA,WBを決めるべきか?
この場合電圧計の違いは最小メモリだけであるので、これを測定精度と考え、
WA=WB/10とすべきであろう、
これの拡張として 一般に 測定精度 を標準偏差 ![]() と取り、重み
と取り、重み ![]() をとることが行われる、
をとることが行われる、
すなわち、精度の良い実験では ![]() は小さい、よって重み
は小さい、よって重み
![]() は大きい、また
は大きい、また
精度の悪い実験では ![]() は大きい、よって重み
は大きい、よって重み
![]() は小さい、という合理的な重みを与える(なぜ2乗なのかは後で考える)。よって
各種の異なる精度を持つ値 xiの平均値<x>は
は小さい、という合理的な重みを与える(なぜ2乗なのかは後で考える)。よって
各種の異なる精度を持つ値 xiの平均値<x>は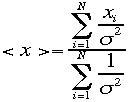 で
計算し、その精度を表す標準偏差
で
計算し、その精度を表す標準偏差![]()
とかかれる。証明はあとで。
例を示そう:もしも測定データxiの組が関数f(x)に従うならさらに、![]() と
いう一次関数のとき:
と
いう一次関数のとき:
つまりxiがばらばらとばらつくときf(x)はどのような振る舞いをするのか?
ばらつきは、標準偏差あるいは分散で表される:fの標準偏差を![]() ,x
の標準偏差を
,x
の標準偏差を![]() として
として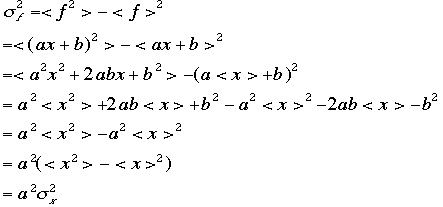 つまり
つまり![]() :そりゃa倍したので、広がりもa倍になる!bは広がりに関与しない。では一
般の関数のときはどうするか?次のテーラー(Talyor)展開の式を使う。
:そりゃa倍したので、広がりもa倍になる!bは広がりに関与しない。では一
般の関数のときはどうするか?次のテーラー(Talyor)展開の式を使う。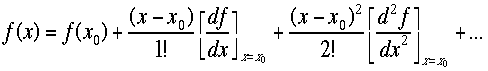 この式は
この式は![]() の近似の成り立つ領域で成立する。ここで、測定値xと書いたが、これがx0付
近であるということは、x0=<x>で有ることを意味している。中心極限定理によりxはガウス分布をしその分散(=標準偏差^2=標準偏差の
2乗)が<x^2>-<x>^2であることも解っている。
の近似の成り立つ領域で成立する。ここで、測定値xと書いたが、これがx0付
近であるということは、x0=<x>で有ることを意味している。中心極限定理によりxはガウス分布をしその分散(=標準偏差^2=標準偏差の
2乗)が<x^2>-<x>^2であることも解っている。
その極意は、どんな関数でもxのべき乗 x^n(xの n乗)で書くことができるという点にある。
例題:次の関数をTalyor展開せよ。![]()
よって、![]() などはとても小さい、よって無視する!!そうす
ると、
などはとても小さい、よって無視する!!そうす
ると、![]() と一次式に持ち込める。すなわち
と一次式に持ち込める。すなわち![]()
![]() よって
よって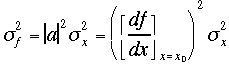 という式を得る。これがより一般化された精度を計算する式である。
という式を得る。これがより一般化された精度を計算する式である。
さらに一般化を進める。つまり、f(x)はいつも変数xだけの関数とは限らないということだ。
が始めからそれをするのは大変なので、2変数つまり![]() つま
り、測定した変数は2個xとyがある時を考える。このとき測定量は(xi,yi)の組として測定されている、例えば、糸と重りで振り子を作る。振り子の振
動の長さを求めるには、糸の長さ(=x)と重りの重心までの距離(おおかた重りの半径)(=y)を測定することになる。さてこの振り子の振動の長さ(
つま
り、測定した変数は2個xとyがある時を考える。このとき測定量は(xi,yi)の組として測定されている、例えば、糸と重りで振り子を作る。振り子の振
動の長さを求めるには、糸の長さ(=x)と重りの重心までの距離(おおかた重りの半径)(=y)を測定することになる。さてこの振り子の振動の長さ(![]() )
で計算されるはずだ。このxとyの測定はそれぞれ行われそれぞれの平均値<x>,<y>と分散(あるいは標準偏差)が判っている
時、振り子長さの値とその精度はどうやって計算すべきかという問題である。ここでも最も簡単な仮定から始める。すなわち
)
で計算されるはずだ。このxとyの測定はそれぞれ行われそれぞれの平均値<x>,<y>と分散(あるいは標準偏差)が判っている
時、振り子長さの値とその精度はどうやって計算すべきかという問題である。ここでも最も簡単な仮定から始める。すなわち![]() とかかれるときの分散の計算となる。もちろんx,yが変動する可能性があり、
その結果がfにどのように伝わるかを計算する事になる。fのばらつきは、標準偏差あるいは分散で表される:fの標準偏差の二乗(分散)を
とかかれるときの分散の計算となる。もちろんx,yが変動する可能性があり、
その結果がfにどのように伝わるかを計算する事になる。fのばらつきは、標準偏差あるいは分散で表される:fの標準偏差の二乗(分散)を![]() ,xの標準偏差の二乗(分散)を
,xの標準偏差の二乗(分散)を![]() 、y
の標準偏差の二乗(分散)を
、y
の標準偏差の二乗(分散)を![]() としよう。
としよう。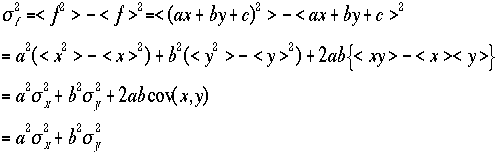 xとyは独立しているので、cov(x,y)=0であるので、独立2変数に
拡張した精度の伝搬式が得られた。これによるとf=ax+by+cのときfの精度を決めるのはaとbであり、2乗和で効いてくる。2乗和ではfの精度(
xとyは独立しているので、cov(x,y)=0であるので、独立2変数に
拡張した精度の伝搬式が得られた。これによるとf=ax+by+cのときfの精度を決めるのはaとbであり、2乗和で効いてくる。2乗和ではfの精度(![]() )は
)は![]() >
>![]() 、
、![]() である(a,b>1のとき)。つまりfの相対精度(
である(a,b>1のとき)。つまりfの相対精度(![]() )は必ずxの相対精度(
)は必ずxの相対精度(![]() )より、yの相対精度(
)より、yの相対精度(![]() )より悪くなる(大きくなる)ことが示めされる。各自計算せよ。
)より悪くなる(大きくなる)ことが示めされる。各自計算せよ。
さらに一般化する、すなわち複数変数の関数f(x,y)時へ拡張する。つまり、測定結果fを得るために、x,やy等を測定しなければならず、x,
yは測定結果であるので、精度を持つ。またTalyor展開を使いたいが、多変数のTalyor展開はどうするかが問題である。一変数のTalyor展開
を次のよう書いた。![]()
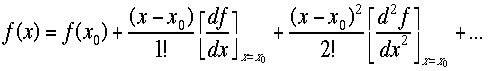 これを独立な2変数へ拡張して次のように書く、
これを独立な2変数へ拡張して次のように書く、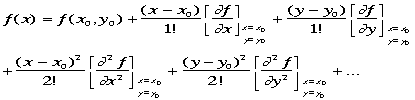 独立な2変数のtaylor展開式の中の
独立な2変数のtaylor展開式の中の![]() や
や![]() はなにか。
はなにか。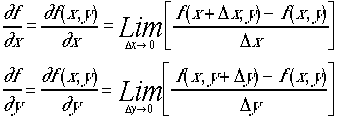 である、これが定義であるが、実際が重要なので、例題をあげる
である、これが定義であるが、実際が重要なので、例題をあげる
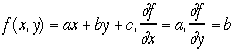 これを偏微分という、大学1年生の後期に微分
積分の中で習うことになっているのだ。
これを偏微分という、大学1年生の後期に微分
積分の中で習うことになっているのだ。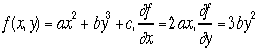
![]()
![]()
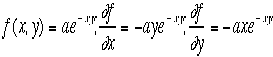
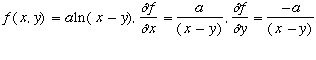
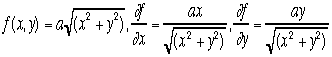 ここまでできればまあ使い物になる。その極意が偏微分でxで(偏)微分すると
きは,yは定数と思っているし、反対にyで(偏)微分するときは,xは定数と思っているのだ。
ここまでできればまあ使い物になる。その極意が偏微分でxで(偏)微分すると
きは,yは定数と思っているし、反対にyで(偏)微分するときは,xは定数と思っているのだ。
独立した2変数x,yについて、![]() つま
り、測定した変数は2個xとyがある時を考える。2変数の偏微分を定義したので、
つま
り、測定した変数は2個xとyがある時を考える。2変数の偏微分を定義したので、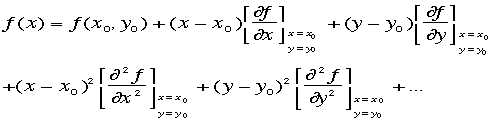 また例によってx-x0,y-y0が0に近いので、近似をつかい、f=ax
+by+cの形にして、
また例によってx-x0,y-y0が0に近いので、近似をつかい、f=ax
+by+cの形にして、
この式からfの標準偏差の二乗(分散)を![]() はx
の標準偏差の二乗(分散)を
はx
の標準偏差の二乗(分散)を![]() 、y の標準偏差の二乗(分散)を
、y の標準偏差の二乗(分散)を![]() から次のようにかかれる
から次のようにかかれる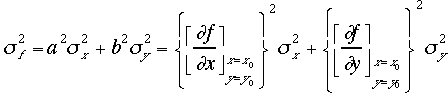 x,yが独立でないときは
x,yが独立でないときは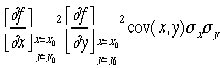 の項が付け加わるが、実際上これを用いることはほとんどない。
の項が付け加わるが、実際上これを用いることはほとんどない。
2変数以上の一般の場合もこれにまねて、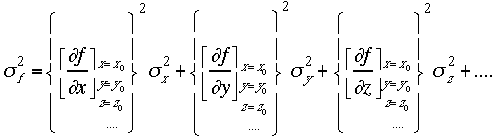 こ
れを精度の伝搬式と呼ぶ(精度を誤差と呼ぶ教科書もある)。
こ
れを精度の伝搬式と呼ぶ(精度を誤差と呼ぶ教科書もある)。
さていよいよ、測定値xの平均値の計算が重み付き平均で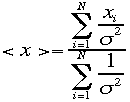 そ
の重みを
そ
の重みを![]() つかい、その精度を表す標準偏差
つかい、その精度を表す標準偏差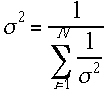 とかく理由を述べる。重みをいまからaiと付けよう。xiの重み付き平均は
とかく理由を述べる。重みをいまからaiと付けよう。xiの重み付き平均は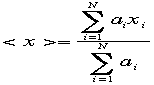 と書くべきである。すなわち重みaiを各データxiにかけて、全部を加えあげ
る、ただし重みは人為的な量なので、これの寄与は分母で相殺しておく、という式である。もちろんこの式が普通に用いられる平均(重みがすべて同じ場合であ
る)と同等であることはおきらかだ。
と書くべきである。すなわち重みaiを各データxiにかけて、全部を加えあげ
る、ただし重みは人為的な量なので、これの寄与は分母で相殺しておく、という式である。もちろんこの式が普通に用いられる平均(重みがすべて同じ場合であ
る)と同等であることはおきらかだ。![]() とい
うαを定義して、平均は
とい
うαを定義して、平均は![]() と書かれる。これをxの関数f(x)と考えて
精度の伝搬式を用いると、
と書かれる。これをxの関数f(x)と考えて
精度の伝搬式を用いると、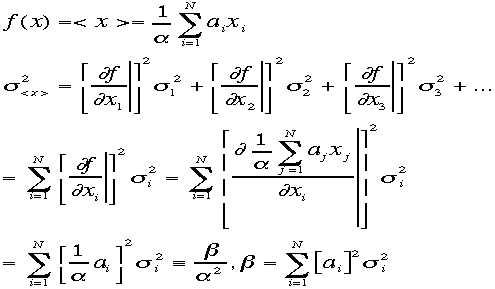 よって問題は最終結果
よって問題は最終結果![]() を最小にする重み
を最小にする重み![]() をどう取れば良いのかという問題に帰着させる事ができる。
をどう取れば良いのかという問題に帰着させる事ができる。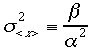 とかきかえて、
とかきかえて、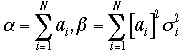 なので、
なので、![]() は
は![]() の関数であるという事にする。すると、
の関数であるという事にする。すると、![]() が極小値をとる
が極小値をとる![]() をを求めなさいという問いで、算数の問題とできる。この答えは
をを求めなさいという問いで、算数の問題とできる。この答えは![]() を
を![]() で微分してゼロになる点を探す作業になる。が、aiはたくさんあるので、微分は
偏微分となる。
で微分してゼロになる点を探す作業になる。が、aiはたくさんあるので、微分は
偏微分となる。![]()
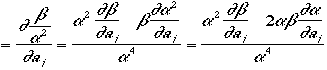 ここで
ここで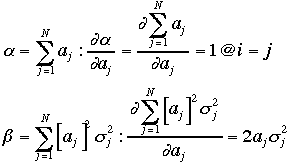 よって
よって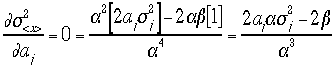
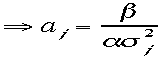 と決定できる、また規格化条件を付けて(本来重み
と決定できる、また規格化条件を付けて(本来重み![]() は全部が同じ場合でも1でも10でも良いので、
は全部が同じ場合でも1でも10でも良いので、![]() としてしまう。よって、
としてしまう。よって、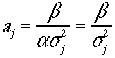
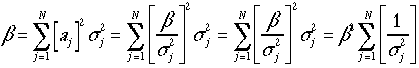
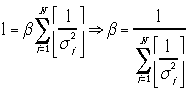 から
から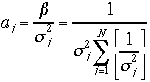 最終的に<x>は
最終的に<x>は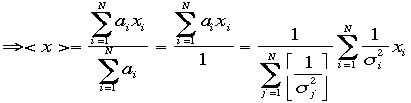 で最初の式が完成する。また
で最初の式が完成する。また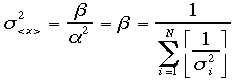 となる。
となる。
精度の伝搬式で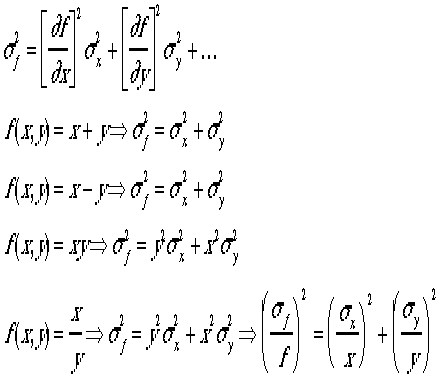 より最後の式は相対精度の計算式で例えばx
の相対精度が3%、yの相対精度が4%であるならば、fの相対精度は5%であり、xの相対精度より、yの相対精度より、悪い。
より最後の式は相対精度の計算式で例えばx
の相対精度が3%、yの相対精度が4%であるならば、fの相対精度は5%であり、xの相対精度より、yの相対精度より、悪い。
問題:2つの抵抗を測定しました。その結果はそれぞれ、15.3+-0.4オーム,24.8+-0.7オーム
であった。これら2つの抵抗を直列につないだ結果は何オームになるか?また並列の場合はどうか?
問題:ある山の高さを測定して、仰角を27.8°、27.3°、28.2°、26.9°、27.5°という結果を得た。また山の頂上からの距離を地図から
945m、971m、912m、954m、982mと得た。山の高さとその精度を考えよ。
問題:x=76.3+-2.1,y=101.4+-4.2とのき、f(x,y)=x+yとその精度を計算せよ。またf(x,y)=x*yの時を計算せよ。
さらにf(x,y)=x/yの場合を計算せよ。
f(x,y)=x*y/sqrt(x*x+y*y)の時はどうか?
問題: 重力定数gを振り子を使って測定せよ。 振り子の実験では振り子の長さxと振動の周期 Tを測定量として、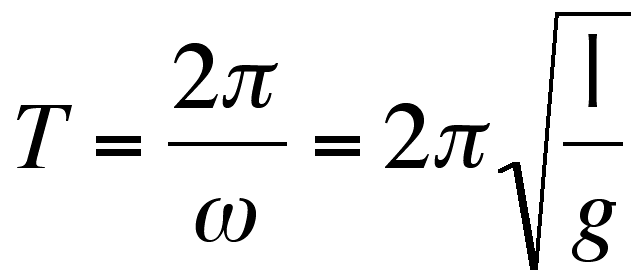 という関係がある。この式を使え。
という関係がある。この式を使え。
問題: 摩擦のない斜面を滑り落ちる物体の位置と時刻を測定して重力加速度を求めよ。
解の例